|
Una retta può assumere tre posizioni rispetto ad
una circonferenza:
| 1 |
esterna |
se
circonferenza e retta non hanno punti in comune |
| 2 |
secante |
se
circonferenza e retta hanno due punti in comune |
| 3 |
tangente |
se
circonferenza e retta hanno 2 punti coincidenti in comune |
Algebricamente il problema delle mutue posizioni
circonferenza-retta si risolve cercando le soluzioni del sistema:
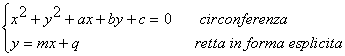
| sostituendo
si ottiene
|
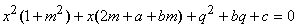 |
le cui soluzioni rappresentano le ascisse dei
punti di intersezione tra la retta e la circonferenza. Per questa equazione di
secondo grado distinguiamo tre casi:
| caso
1 |
D
>
0 |
retta
secante |
| caso
2 |
D
<
0 |
retta
esterna |
| caso
3 |
D
= 0 |
retta
tangente |
Lo
stesso problema può essere affrontato utilizzando l'espressione della retta in
forma implicita: ax+by+c=0.
|