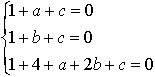Si definisce circonferenza:
L'insieme dei punti P(x,y) del piano cartesiano XOY la cui distanza dal centro
![]()
è una costante che è il raggio R.
( nella figura puoi spostare, agendo col mouse, il centro e variare il raggio)
Dalla definizione segue che (x- a)2+(y-b)2= R2
sviluppando i quadrati ed ordinando: x2+y2-2ax-2by+a2+b2-R2=0 [1]osserviamo che l'equazione della circonferenza contiene:
| due termini quadratici in x e y | x2+y2 |
| due termini lineari in x e y | -2ax-2by |
| un termine noto | a2+b2-R2 |
| osserviamo l'assenza del termine rettangolare | xy |
L'equazione è riconducibile alla forma x2+y2+ax+by+c=0. [2]
Una circonferenza è quindi determinata da tre parametri a,b,c. Questo comporta generalmente che per trovare l'equazione di una determinata circonferenza è necessario disporre di 3 condizioni che si "traducono" in un sistema di 3 equazioni in 3 incognite, risolto il sistema si determinano i tre parametri: a,b e c.
Sostituendo ascisse e ordinate dei tre punti A, B e C nell'equazione [2], si ottiene il sistema
La circonferenza cercata è quindi x2+y2-2x-2y+1=0
|
Dal confronto della [1] con la [2] si ottengono:
| 1) a = -a/2 e b = -b/2 e quindi C(-a/2,-b/2) |
quest'ultima relazione implica che un'equazione del tipo x2+y2+ax+by+c=0 individua una circonferenza solo se a2+b2- 4c ³ 0.