Uno dei primi risultati nella matematica occidentale che non fosse già noto ai greci fu ottenuto nella prima metà del Cinquecento (1515) dal bolognese Scipione del Ferro: un metodo generale per la risoluzione delle equazioni di III grado. Egli però comunicò la sua scoperta solo a un suo allievo, Antonio Maria Fiore; e tuttavia Nicolò Tartaglia, nato a Brescia intorno al 1500, giunse allo stesso risultato indipendentemente.	N. Tartaglia
Nel 1545 la soluzione dell'equazione di terzo e quarto grado diventò di dominio pubblico con l'uscita dell'Ars magna di Girolamo Cardano, medico, matematico, astrologo e libertino, pavese di nascita .
	Nell'opera l'autore accennava al fatto che la formula per le equazioni di terzo grado gli era stata rivelata da Tartaglia, il quale tuttavia lo accusò di aver tradito la promessa di mantenerne il segreto; per questo iniziò un violento e lungo dissidio tra i due. G. Cardano

Un'equazione del tipo x³+ax²+bx+c = 0 si può sempre riscrivere, con metodo di "completamento del cubo", nella forma (x+a/3)³ = A·(x+a/3) + B.

A sua volta un'equazione di III grado della forma x³=ax+b può essere risolta cercando le soluzioni nella forma u+v.

Si trova allora u³ + v³+ 3uv(u+v) = a·(u+v)+b e quindi 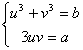o anche 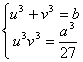da cui u³ e v³ sono soluzioni dell'equazione t²–bt+a³/27 = 0.

Le formule che si ottengono, però, non funzionano sempre: ad esempio, provando con x³ = 15x+4, che ha 4 come soluzione, si giunge all'equazione t² - 4t + 125 che non ha soluzioni reali.