3. Matrice di una trasformazione lineare
Il segmento orientato di vertici (a,c) (b,d) - che in Cabri potremmo rappresentare nascondendo il secondo estremo in modo da sembrare una freccia o scegliendo per il secondo estremo un colore diverso dal nero - è univocamente associato alla trasformazione lineare che definisce. Esso può esser visto come rappresentazione geometrica dell'oggetto detto matrice della trasformazione, usualmente scritta nella forma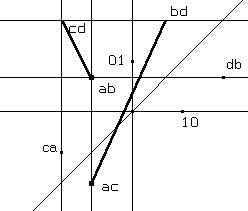
; il primo punto del segmento orientato rappresenta la prima colonna, il secondo punto la seconda colonna.
Le operazioni sulle matrici sono così interpretabili come operazioni tra segmenti. Ad esempio la trasposta della matrice rappresentata dal segmento orientato di estremi (a,c) e (b,d) è la matrice rappresentata dal segmento orientato di estremi (a,b) e (c,d).
Dunque una matrice simmetrica (fig. 11) è rappresentata dalla diagonale di un rettangolo con lati paralleli agli assi e con uno degli altri due vertici sulla bisettrice principale.
.
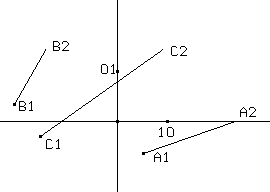
E' noto che il determinante di una matrice si può vedere geometricamente come area del parallelogramma che corrisponde, nella trasformazione lineare definita da quella matrice, al quadrato di vertici O, (0,1), (1,0) e (1,1). Si può anche osservare che il corrispondente del punto (d,c) nella trasformazione di matrice A rappresentata dal segmento orientato di estremi (a,b) e (c,d) è il punto (detA,0).Particolarmente semplice (fig. 12) è la costruzione della somma tra matrici: se A è rappresentata dal segmento orientato A1A2 e B dal segmento orientato B1B2, allora A+B è rappresentata dal segmento orientato C1C2, essendo C1 il simmetrico di O rispetto al punto medio tra A1 e B1 ed essendo C2 il simmetrico di O rispetto al punto medio tra A2 e B2.
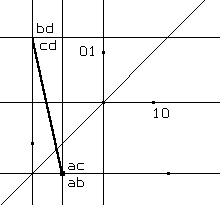
E' anche possibile raffigurare geometricamente (figg.13a e 13b) gli autovalori della matrice A: un numero reale è un autovalore per la matrice A quando, indicando con I la matrice della trasformazione identica, si ha che det(A+I) = 0, ovvero che la matrice A+I è rappresentata da un segmento orientato allineato con O.
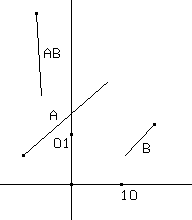
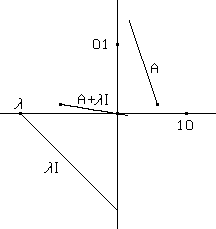La composizione di trasformazioni lineari (fig.14) è legata all'operazione prodotto di matrici: se A è rappresentata dal segmento A1A2 e B dal segmento B1B2, allora la composizione delle trasformazioni associate alle due matrici ha per matrice il prodotto A·B rappresentato dal segmento orientato di estremi A(B1) e A(B2).
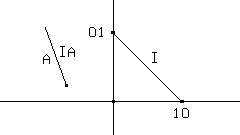
Si può verificare facilmente la non commutatività del prodotto, ed osservare l'esistenza di un elemento neutro (fig. 15), la matrice I rappresentata dal segmento orientato di estremi (1,0) e (0,1).
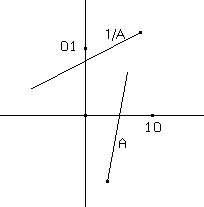
La matrice inversa di una matrice data (fig 16.) è la matrice rappresentata dal segmento orientato che ha per vertici i punti corrispondenti di (0,1) e (1,0) nella trasformazione lineare inversa della trasformazione lineare associata alla matrice data.
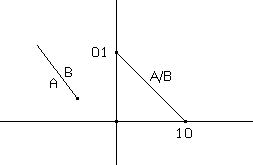
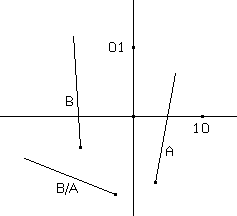
Se A-1 è la trasformazione lineare inversa della trasformazione lineare di matrice A e B è la matrice rappresentata dal segmento orientato B1B2, allora la matrice rapporto A/B , che potremmo indicare anche B/A, è rappresentata (fig 17) dal segmento orientato di estremi A-1(B1) e A-1(B2).
Si può vedere in particolare (fig. 18) che A-1A = I.
