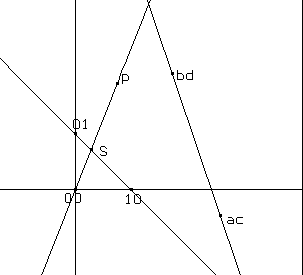
1. Costruzioni di base
Una trasformazione lineare è una trasformazione nel piano che a punti fa corrispondere punti e con le seguenti proprietà:Figura 1 
Figura 2 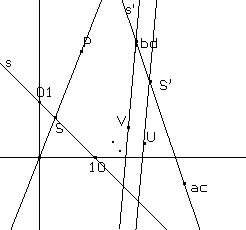
Figura 3 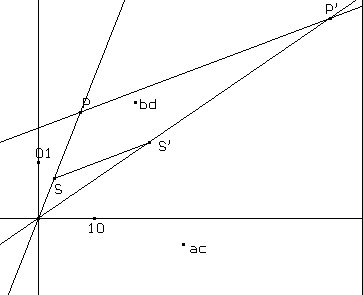
Una tale costruzione può essere facilmente realizzata con Cabri e diviene sufficientemente stabile anche per i casi limite per i quali la costruzione descritta è impossibile.
Preliminarmente saranno creati, in particolare, i punti (1,0) e (0,1), i punti (a,c) e (b,d) ad essi corrispondenti , ed inoltre il punto variabile P del quale costruire il corrispondente:Creare un punto (Creazione/Punto) Indicare con O il punto appena costruito (Edizione/Nomi) Creare un punto (Creazione/Punto) Indicare con 10 il punto appena costruito (Edizione/Nomi) Creare un punto (Creazione/Punto) Indicare con 01 il punto appena costruito (Edizione/Nomi) Creare il punto corrispondente di 10 nella trasformazione lineare (Creazione/Punto) Indicare con ac il punto appena creato (Edizione/Nomi) Creare il punto corrispondente di 01 nella trasformazione lineare (Creazione/Punto) Indicare con bd il punto appena creato (Edizione/Nomi) Creare un punto (Creazione/Punto) Indicare con P il punto appena creato (Edizione/Nomi)Nel seguito della costruzione si realizza il 1° passo del metodo indicato:
Creare la retta s per 10 e 01 (Creazione/Retta per 2 punti) Creare la retta s' per ac e bd (Creazione/Retta per 2 punti) Creare la retta per O e P (Creazione/Retta per 2 punti) Costruire il punto S comune alle rette s e OP (Costruzione/Intersezione di 2 oggetti)Nel seguito della costruzione si realizza il 2° passo del metodo indicato:
Costruire il punto medio tra 01 e ac (Costruzione/Punto medio) Costruire il punto V simmetrico di 10 rispetto al punto medio appena costruito (Costruzione/Simmetrico di un punto) Costruire il punto medio tra S e ac (Costruzione/Punto medio) Costruire il punto U simmetrico di 10 rispetto al punto medio appena costruito (Costruzione/Simmetrico di un punto) Creare la retta di estremi V e bd (Creazione/Retta per due punti) Costruire la retta parallela per U a tale segmento (Costruzione/Retta parallela) Costruire il punto S' comune a questa e alla retta s' (Costruzione/Intersezione di 2 oggetti)Nel seguito della costruzione si realizza il 3° passo del metodo indicato:
Creare il segmento di estremi S e S' (Creazione/Segmento) Costruire la retta per P parallela a tale segmento (Costruzione/Retta parallela) Creare la retta OS' (Creazione / Retta per 2 punti) Costruire il punto comune a queste ultime due rette (Costruzione/Intersezione di 2 oggetti Indicare con P' il punto appena costruito (Edizione/Nomi)Una tale costruzione può divenire infine macrocostruzione Cabri, che è possibile memorizzare su disco e far comparire come opzione del menu Costruzione,da utilizzare per costruire direttamente il corrispondente di un punto o dei vertici di una spezzata:
Registrare la macrocostruzione (Macrocostruzioni/Nuova/selezionare nell'ordine: punti O, 10, 01, ac, bd e P / fine degli oggetti iniziali / selezionare il punto P'/ fine degli oggetti finali / nominare T(P) la macro / registrare un messaggio di aiuto come: "Indicare in questa successione: i punti O, 10, 01, ac, bd, il punto P . Il punto costruito è corrispondente di P nella trasformazione lineare che ai punti 10 e 01 fa corrispondere rispettivamente ac e bd" / salvare su disco la macro / scegliere ad esempio la directory MACRO e digitare il nome TRASFLIN)Osserviamo che la costruzione proposta è invertibile; infatti, a parte alcuni casi limite, si può:
dato P', costruire S' sulla retta per (a,c) e (b,d), costruire sulla retta per (1,0) e (0,1) il punto S di cui S' è il corrispondente, costruire P come intersezione della retta OS e della retta per P' parallela a S'S;così si può realizzare anche una macrocostruzione Cabri per la trasformazione lineare inversa di una trasformazione lineare data, assegnata mediante i punti (a,c) e (b,d) corrispondenti rispettivamente dei punti (1,0) e (0,1).