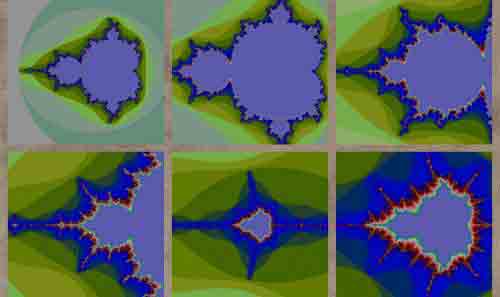
I frattali sono oggetti geometrici che presentano una struttura complessa e dettagliata a ogni livello di ingrandimento. Godono della proprietà d’invarianza di scala, in altre parole essi sono "autosomiglianti", cioè ogni piccola porzione del frattale può essere vista come una riproduzione su scala ridotta dell’intera figura.

Attualmente si conoscono e si possono costruire vari tipi di figure con caratteristiche simili, cioè "autosomiglianti", ma è facile comprendere come, nel momento in cui esse per la prima volta furono studiate nel XIX secolo, sembravano solo oggetti curiosi e bizzarri.Una svolta nello studio sull’argomento si ebbe negli anni Sessanta, con la scoperta della geometria dei frattali da parte del matematico francese di origine polacca Benoit B. Mandelbrot. Egli adottò una definizione più astratta di dimensione, rispetto a quella usata nella geometria euclidea, affermando che per dimensioni di un frattale si dovesse intendere l’esponente della misura delle sue dimensioni fisiche.

Il risultato è che il frattale non può essere considerato come un’entità avente due, tre, o comunque un numero intero di dimensioni, ma caratterizzata da una dimensione frazionaria. Ad esempio, la dimensione della curva a "fiocco di neve" è 1,2618.

La geometria dei frattali non è semplicemente il frutto di una vera speculazione teorica, ma trova anche interessanti applicazioni. Una costa, se misurata fino nelle sue piccole irregolarità, tenderebbe ad avere uno sviluppo infinito, proprio come la curva a "fiocco di neve".

Mandelbrot suggerì che le montagne, le nuvole, i raggruppamenti di galassie e altri fenomeni naturali potessero essere considerati esempi di frattali naturali; da ciò, l’applicazione della geometria dei frattali alle scienze vide un rapidissimo sviluppo. Inoltre, la bellezza dei frattali li ha resi un elemento-chiave nel campo della grafica per computer.