Risp.
9 - Per
calcolare il dominio di una funzione bisogna tener conto delle
operazioni che compongono la legge assegnata:
|
TIPO
DI FUNZIONE
|
CONDIZIONI
|
OSSERVAZIONI
|
|
Razionale intera:
|
|
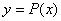
Nessuna
limitazione
|
Tutte
le operazioni in P(x) sono consentite
|
|
Razionale fratta :
|
|
|
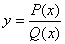
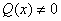
L’unica
operazione non consentita è la divisione per 0. Occorre
scartare dal dominio i valori di x che annullano il
denominatore.
|
|
Irrazionale :
|
|
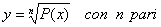
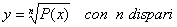
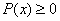
nessuna limitazione
|
Solo quando l’indice di radice n è pari ci
possono essere problemi di estrazione di radice e in tal
caso il radicando P(x) deve essere positivo o nullo.
|
|
Logaritmica :
|
|
|
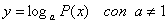
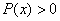
Il logaritmo deve avere l’argomento >0
|
Esempi:
a)
FUNZIONI RAZIONALI INTERE:
|
1)
D = R
per cui
f :
D →
R
x
→
|
|
|
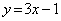
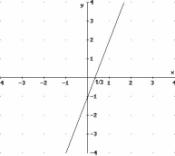
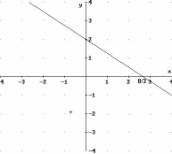
2)
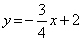
D = R
per cui
f :
D →
R
x
→
|
|
|
|
|
|
|
|
|
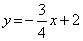
3)
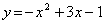
D = R
per cui
f : D → R
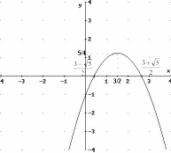
x → y=-x2+3x-1
|
|
|
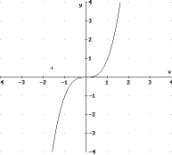
4)
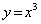
D = R
per cui
f : D → R
x →
|
|
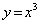
b)
FUNZIONI RAZIONALI FRATTE
Se la funzione è razionale fratta l’unica
operazione non consentita è la divisione per zero per cui occorre
scartare dal dominio i valori di x che annullano il denominatore.
|
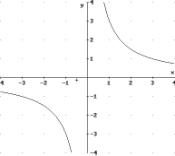
5)
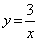
si pone x¹0
e pertanto
D = ]-¥,0[
È ]0,+¥[
per cui
f : D → R
x → y = 3/x
|
|
|
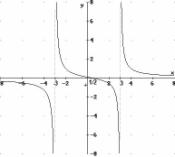
6)
si pone x2-9¹0 cioè x¹±3
D=]-¥,0[
È ]-3,3[ È
]0,+¥[
per cui
f : D → R
x → y=(2x-1)/(x2-9)
|
|
c)
FUNZIONI IRRAZIONALI :
Nel caso di funzioni irrazionali occorre
distinguere due casi: 1) l’indice di radice è pari; 2) l’indice di radice è dispari.
Solo nel primo caso (indice pari) possono presentarsi
problemi nell’estrazione di radice (non esiste la radice di
indice pari di un numero negativo), bisognerà allora imporre al
radicando di essere ³ 0; nel secondo caso il dominio sarà tutto R.
|
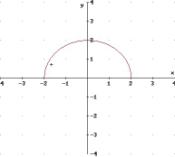
7)
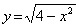
D = [-2 , 2]
per cui
f : D →
R
x →
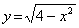
si
pone
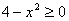e si risolve la
disequazione di 2° grado: -x2+4³0
D>0,
a discorde con ³
Essa
è verificata per
-2 £ x £
2
|
|
|
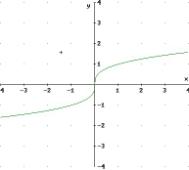
8)
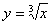
l’indice di radice 3 è dispari per cui non ci
sono limitazioni
D
= R
per cui
f : D →
R
x →
|
|
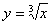
d)
FUNZIONI
LOGARITMICHE:
Ricordando che esiste solo il logaritmo di un numero
maggiore di zero, nelle funzioni logaritmiche occorre porre
di conseguenza l’argomento maggiore di zero.
|
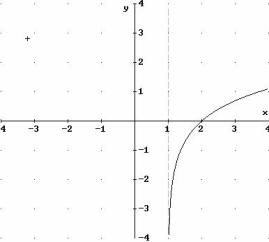
9)
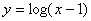
si pone
x – 1 > 0
e si risolve la disequazione di primo grado:
x > 1
Þ D = ]1 , +¥[
f : D → R
x →
|
|
|
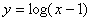
