Per stabilire l'interbinario del nostro plastico abbiamo pensato di procedere per via matematica per calcolare la distanza minima consentita dagli ingombri laterali dei mezzi circolanti.
Per calcolare l’ingombro massimo dei rotabili dobbiamo tenere presente due effetti:

• lo “spanciamento” verso l’interno del centro del rotabile che transita sul binario esterno
• lo "sbandieramento" verso l’esterno delle estremità del rotabile che transita sul binario interno.

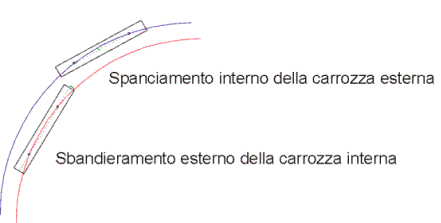
  Per sicurezza dobbiamo calcolare questi due effetti sommati e in più aggiungere una distanza minima di franco.

  1. Una carrozza sul binario esterno che “spancia” verso l’interno ha uno scostamento dall’asse del binario tanto maggiore quanto maggiore la distanza fra gli interperni ( i perni dei carrelli o gli assi di un carro a due assi) e tanto minore il raggio di curvatura. Pitagora ci da una mano

     Xe= Lo spanciamento interno della carrozza che transita sul binario esterno
     R =Il raggio di curvatura esterno
     I= L’interperno
     

     Xe= R – ( radice quadrata ( R 2 – I/2 2))

  2. Una carrozza sul binario interno che “sbandiera” verso l’esterno ha uno scostamento dall’asse del binario tanto maggiore quanto maggiore è la distanza (sbalzo) dal perno carrello al respingente della carrozza e tanto minore il raggio di curvatura.

     Xi= Lo spanciamento verso l’interno della carrozza interna (calcolato sul raggio di curvatura interno )
     L = La lunghezza della carrozza
     Ri = Il raggio di curvatura interno
     Y = Lo sbandieramento della carrozza interna verso l’esterno

     Y =(radice quadrata ( L/2 2 + (Ri-Xi) 2 )) – Ri

  Lo sbalzo di una motrice di un elettrotreno potrebbe creare problemi in curve molto strette

  Ovviamente per calcolare l’ingombro effettivo del rotabile, in entrambi i casi bisogna aggiungere le dimensioni di mezza carrozza, per cui l’interbinario minimo risultante sarà la somma di

  Xe+Y+ larghezza rotabile

  Per mettermi nelle peggiori condizioni ho misurato l’interperno della carrozza più lunga che ho trovato (carrozza ristorante DB) lunghezza mm315 interperno mm220. Ho immaginato che due di queste carrozze si trovassero contemporaneamente sulla stessa curva , e in più ho aggiunto uno spazio franco di 2 millimetri , ecco il risultato nella tabella che segue.
   

   
   

  Calcolo ingombri e interbinario (misure in millimetri)
  Carrozza ristorante DB
  Lunghezza carrozza		315
  Larghezza carrozza		34
  Interperno carrozza		220		sicurezza	2
  Raggio di curvatura esterno	Spanciamento interno della carrozza esterna		Raggio interno	Spanciamento interno carrozza interna	Sbandieramento esterno carrozza interna		interbinario minimo
  2000	3,03		1950	3,11	3,26		42,08
  1750	3,46		1700	3,56	3,73		42,99
  1500	4,04		1450	4,18	4,37		44,21
  1300	4,66		1250	4,85	5,07		45,53
  1000	6,07		950	6,39	6,66		48,53
  950	6,39		900	6,75	7,03		49,22
  900	6,75		850	7,15	7,44		49,99
  850	7,15		800	7,60	7,90		50,85
  800	7,60		750	8,11	8,42		51,82
  750	8,11		700	8,70	9,02		52,93
  700	8,70		650	9,38	9,70		54,20
  650	9,38		600	10,17	10,50		55,67
  600	10,17		550	11,11	11,43		57,40
  550	11,11		500	12,25	12,55		59,46
  500	12,25		450	13,65	13,90		61,95

  I dati della tabella ci hanno molto confortato perché ci lasciavano molta libertà nell’avvicinare le rotaie. Avevamo già stabilito che il raggio minimo di curvatura visibile fosse di 1500 millimetri ( quello che succede nei meandri delle gallerie e nelle stazioni fantasma non è dato da sapere) e quindi potevamo permetterci un avvicinamento fino a 45mm.

  Le prove pratiche, dopo aver fissato qualche flessibile su una tavola, confermavano questi risultati anche se non nego un po’ di batticuore causato dal fatto ché non siamo abituati a vedere i nostri modelli sfiorarsi così da vicino, ma se volevamo riprodurre la realtà questa era la strada giusta.
  Nella realtà l’interbinario è di 350 centimetri per le ferrovie costruite anteguerra (sulla Pontremolese è di 385 cm) e di 400 cm per le tratte rifatte o costruite successivamente. In scala H0 400 cm sono esattamente 45,97.
  Per rispettare la realtà quindi 46 millimetri di interbinario potrebbe essere una misura perfetta, con raggi di curvatura superiori a 1300 millimetri i rotabili (quelli in scala HO) sono in sicurezza e il realismo è massimo
  Ma alcune considerazioni di carattere prudenziale ci hanno portato ad allargare ancora questa misura. Innanzi tutto i giochi e i laschi che si possono incontrare sui rotabili fra rotaia e ruota, fra ruota e carrello, fra carrello e cassa, sommati nel senso più sfavorevole fra due rotabili che si incrociano, potrebbero superare quel franco di appena 2 mm considerato. Inoltre dovremmo anche considerare alcuni banali incidenti come un semplice asse sviato, o un asse fuori sede che fa inclinare la vettura, o mille altre disavventure che, in un plastico sociale dove molti possono metterci le mani, possono sempre accadere. Ma soprattutto non vogliamo costruire un plastico visto con troppa diffidenza dai soci
  La norma NEM 102 “Sagoma di libero passaggio in rettilineo" stabilisce una larghezza limite di 48 millimetri. E’ vero che si contraddice con la norma NEM 112 ma tutto sommato è bene attenersi anche perché due millimetri in più di spazio franco non dispiace a nessuno, e quindi non ci sono più dubbi ecco la misura dell’interbinario del nostro plastico, è deciso:

   48 millimetri
  e tutti i calcoli finora eseguiti? Sono serviti a godere i sonni tranquilli del giusto.

  DISTANZE DEI PALI

  Misure standard

  

  Dopo aver stabilito l'interbinario abbiamo ragionato con gli stessi metodi per decidere la distanza dei pali della linea aerea dai binari.    Al vero si osservano le seguenti misure (la distanza è misurata fra il bordo interno della rotaia e la superficie esterna del palo considerando eventuali ingombri di contrappesi o sezionatori) :

   Nella realtà:
   

  Piena linea rettifilo	170 cm
  Piena linea curva raggio =< 1500m	200 cm
  Nei pressi di PL per 100 m	200 cm
  Prima dei segnali per 200 m	200 cm
  In stazione sui marciapiedi	250 cm dal bordo del marciapiede

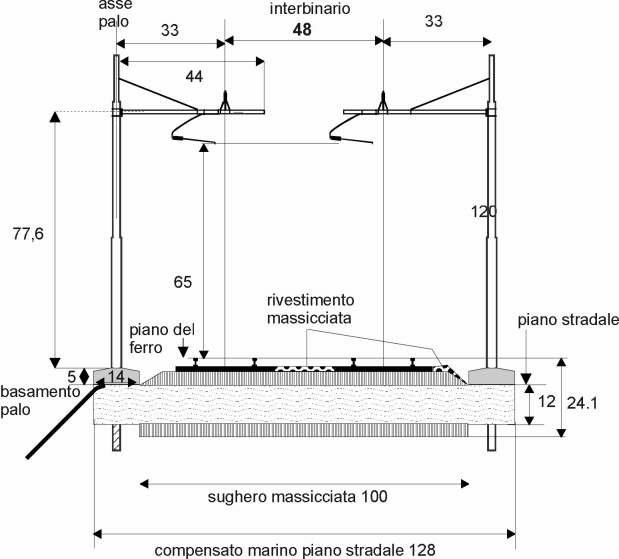
  Sul plastico:

  Considerando che sul nostro plastico la piena linea in rettilineo è praticamente inesistente (la Pontremolese è una linea di montagna) abbiamo pensato di unificare le distanze dei pali dalla rotaia per tutto il plastico come riportato in figura. Le misure rispettano la realtà in scala H0. La distanza dell'asse del palo dall'asse del binario di 33 mm si ottiene sommando:
  1,5 (metà palo) + 8,25 (metà scartamento) + 23 (la distanza in scala 1/87 di 200cm) = 32,75 mm

                    Asse palo - asse binario = 33 millimetri

                           Piano stradale = 128 mm

                               Massicciata =  100 mm
   

  La Fotoincisione

  Interbinario

  Il ponte sul Verde

  La Struttura portante

  La linea aerea

  Home page

  Mettiti in contatto con noi via E-Mail