
CAPITOLO VI
Stabilità e forma
Nel capitolo precedente abbiamo visto che l'atmosfera gioca un ruolo molto importante nel volo di un modello e abbiamo toccato con mano gli effetti negativi dovuti alla resistenza che ne deriva. Per costruire qualcosa di ben fatto e avvicinarsi cosi a quello che potremmo chiamare " comportamento ottimale ", è necessario ricorrere a un progetto appropriato e a una costruzione opportuna: a questo scopo è stato svolto negli anni passati un gigantesco lavoro di ricerca teorica e sperimentale su modelli in volo.
Come premessa essenziale dobbiamo ricordare che un razzo in volo è un corpo libero nello spazio, e non un veicolo vincolato al suolo: non c'è quindi da meravigliarsi se è impossibile riprodurre il suo comportamento, facendo riferimento a un mezzo " terrestre "; in particolare va messo in evidenza che le sue possibilità di movimento sono molteplici.
Per semplicità, e per facilitare la comprensione del comportamento di un razzo in volo, si può assumere che ogni moto sia la risultante di altri sei moti separati, come la fig. 53 mostra. C'è cosi la spinta dovuta al motore e che tende a far muovere il modello in avanti, mentre la resistenza dovuta all'atmosfera e il peso del veicolo hanno un effetto contrario. C'è poi il moto di imbardata che fa muovere l'ogiva a destra o a sinistra, la picchiata e l'impennata, che la fanno puntare, rispettivamente, verso il basso e verso l'alto. Infine c'è il moto di rollio quando il modello ruota attorno al proprio asse longitudinale. Per l'esattezza, l'imbardata, la picchiata e l'impennata possono essere considerate tre varianti dello stesso tipo di moto, perché quasi tutti i modelli, a eccezione di quelli predisposti per il volo veleggiato, sono simmetrici rispetto al loro asse.
Mentre la spinta e la resistenza producono moti lineari, cioè moti che avvengono lungo una retta, tutti gli altri sono moti di tipo rotazionale. Poiché ogni corpo che ruota, o che gira su se stesso, deve avere un asse di rotazione, asse inteso come una linea immaginaria intorno alla quale si muove, possiamo parlare di asse di impennata-picchiata, di asse di imbardata e di asse di rollio, tutti perpendicolari fra loro.
Come abbiamo già visto, il moto può subire variazioni solo sotto l'effetto di una o più forze esterne agenti sul corpo; quando una forza è applicata a un oggetto libero nello spazio in generale tende a farlo ruotare attorno a un opportuno asse di rotazione, che passa per il suo baricentro, o punto di equilibrio. In tutta la meccanica il baricentro, detto anche centro delle forze gravitazionali, o semplicemente CG, è un concetto di fondamentale importanza.
E' possibile convincersi sperimentalmente di quanto detto in una maniera assai semplice. Si prenda un bastone di legno lungo 50 cm circa e lo si metta in equilibrio su una lama affilata: il punto di sospensione coincide con il baricentro, che abbiamo così individuato e che va marcato con un tratto di penna. Se a questo punto si getta il bastone in aria imprimendogli un moto di rotazione attorno a se stesso, si vede abbastanza bene che esso ruota attorno al punto che è stato marcato; il risultato non cambia anche ripetendo la prova con tecniche di lancio diverse.
Se uno prende un po' di mastice e lo sistema all'estremità del bastone si accorge che il baricentro si è spostato, avvicinandosi all'estremità dove è stato aggiunto il peso; se adesso si ripete l'esperimento di prima, equilibrando di nuovo il bastone, e una volta segnato il baricentro lo si getta in aria come già descritto, si può costatare che l'asse di rotazione passa per il nuovo baricentro.

Quando si costruisce un modello con l'intenzione di farlo volare, si vuole che esso se ne vada diritto nella direzione verso cui è stato puntato; si vuole evitare nella maniera più assoluta che giri su se stesso come faceva il bastone e che vada soggetto a sbandamenti perché ciò genera un angolo di attacco maggiore e quindi maggiore resistenza. In una parola, il risultato che si vuole ottenere è che il modello voli via diritto e veloce nell'aria, seguendo una traiettoria il più possibile prossima alla verticale. D'altro canto un modello in volo va soggetto all'azione di numerose forze, che tendono a farlo ruotare intorno ai suoi assi trasversali, fra le quali possiamo citare la spinta del vento, una cattiva sistemazione delle pinne stabilizzatrici e un non perfetto allineamento del motore. Poiché effetti di questo genere sono presenti addirittura nei modelli costruiti con tutte le regole, se il progetto non è stato coscienzioso ne risulta senz'altro un volo irregolare non appena il razzo si è staccato dalla rampa di lancio. Ciò che si ottiene è quindi una traiettoria imprevedibile e strana, alla cui fine il modello piomberà a terra con un tonfo, lasciando il costruttore con un mucchietto di carta e di balsa.
Il modello deve vincere queste forze di disturbo producendo una forza atta a mantenerlo in volo rettilineo. Quasi tutti i grandi razzi di Cape Kennedy sono perciò dotati di un sistema di controllo a giroscopio, sensibile a ogni minimo mutamento di rotta e capace di generare un segnale che viene inviato a un calcolatore; quasi istantaneamente si ha un segnale di ritorno che provvede a correggere la rotta nel senso più opportuno. E' evidente che un modellista non può adottare metodi simili, perché complessi, dispendiosi e troppo pesanti per il modello; tutto quello che può fare è ricorrere a un sistema più semplice, per quanto estremamente efficace, che consiste nel dotare il missile di pinne stabilizzatrici: in questo modo la stessa corrente d'aria che investe il velivolo contribuisce a mantenerlo diritto.
Quando un flusso d'aria investe una superficie di fianco, o anche sotto un leggero angolo, si genera una forza resistente che tende a muoverla: tale forza va collegata alla pressione dell'aria.
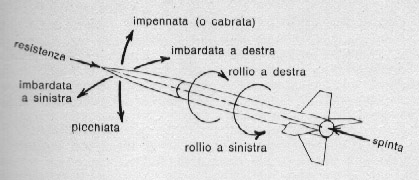
Fig. 53. Forze che agiscono su un modello in volo.
Quando si prende in considerazione la forza peso, si parla di un punto particolare, detto baricentro, dove si possono considerare concentrate tutte le forze gravitazionali agenti sul corpo; il baricentro gode di questa proprietà, di essere cioè l'elemento fondamentale nei problemi di equilibrio. Analogamente in un corpo in movimento esiste un punto, conosciuto come centro delle posizioni, o CP, dove si possono pensare concentrate tutte le forze dovute alla pressione.
Questo fatto è messo in evidenza da una facile prova che richiede ancora l'uso di un bastone di legno. Imperniandolo in corrispondenza del baricentro con un sistema che presenti scarso attrito e mantenendolo in una corrente di aria mossa da un ventilatore, ci si accorge che il bastone non ruota per effetto della pressione dell'aria; questo è vero solo se è simmetrico, indipendentemente dalla posizione angolare che gli è stata data prima della prova. Questo significa anche che il centro delle pressioni coincide con il baricentro, il che comporta l'assenza di forze stabilizzatrici dovute alla pressione dell'aria Se riportiamo queste condizioni in un modello, la presenza di pinne non basta a generare una forza capace di mantenerlo in volo rettilineo: in pratica la traiettoria risulta ancora incontrollata e imprevedibile.
Prendiamo ora un piccolo pezzo di cartoncino sagomato e incolliamolo o leghiamolo a una estremità del bastone, sospendendo quest'ultimo in corrispondenza del suo nuovo baricentro in maniera analoga a quanto fatto prima. Se accendiamo il ventilatore, il bastone ruoterà mettendo l'estremità dove è stato incollato il cartoncino nella direzione opposta a quella da cui arriva la corrente d'aria. Questo fatto è spiegabile perché l'area relativamente maggiore presentata al vento da un'estremità è per forza di cose soggetta a una spinta maggiore.
Se ora si cambia il punto di sospensione, si finisce col trovarne uno per cui il bastone non ruota più, perché da ambo le parti ci sono forze equivalenti. In questa maniera abbiamo determinato il centro delle pressioni, dotato della proprietà di dividere idealmente il bastone in due parti sulle quali la spinta aerodinamica si rivela di uguale intensità.
Se ora si cambia il punto di sospensione avvicinandolo ulteriormente al cartoncino, l'effetto che si ottiene è il contrario di quanto già visto: il bastoncino ruoterà completamente su se stesso, e per fargli riprendere la posizione di prima non c'è altro mezzo che aumentare l'area di quella specie di pinna che abbiamo aggiunto. In questo modo si sposta di conseguenza il centro delle pressioni, che ritorna cosí a trovarsi sulla parte del bastone compresa fra il punto di sospensione e quello di maggior resistenza (pinna aggiunta).
Gli esperimenti che abbiamo ora descritti sono molto significativi, perché un modello si comporta esattamente nella stessa maniera, tenendo presente che il suo corpo corrisponde al bastone e le pinne stabilizzatrici al pezzo di cartone.
Se sì sospende il modello in corrispondenza del suo baricentro con un sistema di scarso attrito, si vedrà che l'ogiva tende a sistemarsi, magari dopo qualche oscillazione, nella direzione da cui arriva il vento solo se il centro delle pressioni si trova nella parte posteriore del razzo. Questo vuol dire che il volo di un oggetto siffatto è stabile e che è possibile a priori determinarne con esattezza le caratteristiche
In sostanza bisogna fare in modo che il centro delle pressioni si trovi dietro il baricentro; è questa una condizione essenziale, che può essere rispettata giocando su molti fattori, tra i quali possiamo ricordare: forma, profilo, numero e disposizione delle pinne stabilizzatrici, lunghezza del corpo, tipo di ogiva impiegata.
E' abbastanza interessante notare che la posizione del CP può dipendere dall'angolo di attacco: una considerazione di questo genere disorienta il principiante, ma merita di essere fatta, al fine di spiegare alcune " stranezze " che a volte capitano durante il volo.
Difatti, finché l'angolo di attacco si mantiene limitato, il modello può anche essere capace di autocorreggere la propria rotta; ma se per caso l'angolo dovesse superare un valore " critico ", allora si manifesterebbe un'improvvisa instabilità, per cui il razzo girerebbe su se stesso e continuerebbe a volare in questa anomala posizione. Come conclusione possiamo affermare che il centro delle pressioni si sposta in avanti quando l'angolo di attacco aumenta.
Come abbiamo visto, la posizione relativa dei centri di gravità e di pressione determina tre condizioni di volo, delle quali una sola è stabile e che possiamo cosi riassumere:
1. Stabilità positiva, quando il centro delle pressioni è dietro al baricentro; è un po' come se il modello pesasse " sul davanti ", ma, per effetto delle lunghe pinne stabilizzatrici di cui è fornito, potesse volare diritto con qualsiasi condizione di vento.
2. Stabilità neutra, quando i due centri coincidono: questa situazione è caratterizzata da un'ogiva leggera e da piccole pinne. Manca qualunque forza che possa stabilizzare il modello durante il volo, cosi che esiste sempre la possibilità di sbandamenti improvvisi che qualche volta si concludono con una catastrofe.
3. Stabilità negativa, quando il baricentro si trova dietro al centro delle pressioni: in questo caso le forze aerodinamiche tendono a rovesciare completamente il modello. Non appena si manifesta un piccolo angolo di attacco non esiste più la possibilità di raddrizzamento, ma anzi il processo si esalta e il volo è caratterizzato da continui ribaltamenti del razzo su se stesso.
La fig. 54 mette in evidenza queste tre condizioni essenziali di stabilità.
Ricordate sempre la condizione di stabilità del volo attraverso la " regola dell'alfabeto ": la lettera G viene prima della lettera P, la gravità prima della pressione, CG prima di CP.
Prima di far volare un modello, si dovrebbe sempre determinare sperimentalmente la relazione esistente fra i due centri. Per quanto riguarda quello di gravità il compito si presenta abbastanza facile, perché basta trovare le condizioni di equilibrio appoggiando il modello a un sostegno; bisogna solo ricordare che tale ricerca va effettuata una prima volta con un motore ancora inutilizzato, per simulare le condizioni al momento del lancio, e poi con un motore che ha già funzionato, per determinare il comportamento del modello nella fase terminale del volo. Come regola quasi generale, si può affermare che durante il volo " per spinta " il baricentro si sposta in avanti e che perciò la stabilità migliora.
Per quanto riguarda invece il centro delle pressioni la ricerca sperimentale è lunga e difficile: in pratica il modellista non ha a disposizione che il metodo a " sospensione " prima descritto, perché non è in grado di costruire un tunnel a vento efficiente. Spesso poi si sente l'esigenza di determinare il CP per via diversa dalla sperimentale, per il semplice motivo che il modello è solo in fase di progetto.
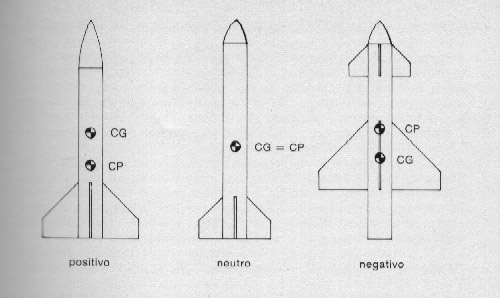
Fig. 54. Relazioni fra baricentro (CG) e centro delle pressioni (CP).
Una via abbastanza comoda per risolvere questo problema è rappresentata dal metodo detto del " centro dell'area laterale ". In pratica si ritaglia in un cartoncino una figura uguale alla sagoma laterale del modello, determinandone poi il baricentro mettendolo, al solito in equilibrio sulla lama di un coltello; il punto cosi trovato è quello che viene comunemente chiamato " centro dell'area laterale " e che può essere praticamente assimilato al CP. In questa ricerca raccomandiamo di ritagliare la figura da un unico cartoncino, perché altrimenti se ne dovrebbero incollare insieme due o tre falsando la distribuzione dei pesi e quindi la posizione del baricentro.
E' possibile anche calcolare ambedue i centri con il " metodo del momento ": per quanto riguarda il baricentro occorre prima determinare o stimare quello delle singole parti - ogiva, corpo, pinne stabilizzatrici, motore, ecc. - e conoscere i relativi pesi. Si moltiplica ora il peso di ogni parte per la distanza dal relativo baricentro, calcolata rispetto a un punto di riferimento unico, determinando così per ogni parte quello che viene definito " momento ". A questo punto si divide il "momento totale " (ottenuto come somma, dei momenti parziali) per il peso complessivo, ottenendo così un numero che ci dà la posizione del centro di gravità sempre rispetto al punto di riferimento considerato. La Tab. 7 riporta un calcolo di questo tipo, assumendo come riferimento l'estremità anteriore dell'ogiva.
Allo stesso modo, si procede per il calcolo del centro delle pressioni con la sola differenza che vanno utilizzati i " momenti delle aree " al posto di quelli dei pesi; di conseguenza vanno presi in considerazione i prodotti delle aree per le distanze dei rispettivi centri da un punto fisso di riferimento; i prodotti vanno sommati tutti quanti e divisi per la somma delle aree o area totale.
Il metodo del momento è sufficientemente preciso e fornisce risultati quasi esatti: in genere l'errore che si commette non raggiunge 1 cm, come qualunque modellista esperto può confermare.
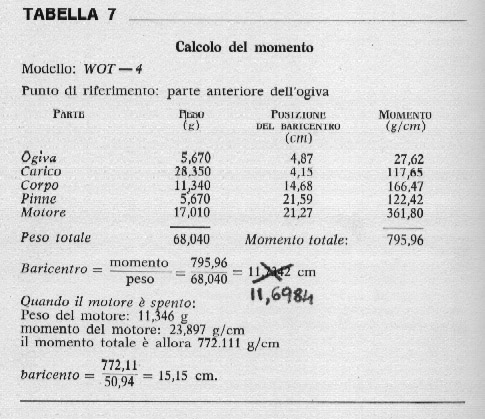
La preferenza va perciò accordata a questo metodo che unisce indiscutibili pregi anche sotto l'aspetto della semplicità.
Anche il " metodo dell'area laterale " è abbastanza attendibile, per quanto l'errore raggiunga a volte proporzioni maggiori; l'esperienza conferma inequivocabilmente che in genere il centro effettivo delle pressioni si trova dietro quello calcolato, a una distanza che si aggira attorno a tre volte il diametro del corpo. Espresso in questi termini l'errore può sembrare notevole, ma ha il pregio di essere " a vantaggio della sicurezza ", tanto per usare un modo di dire tipico dell'ingegnere: questo significa che se in fase di progetto è stata verificata la posizione reciproca dei due centri ed è stata trovata buona non c'è da aspettarsi sorprese, perché semmai il centro delle pressioni si troverà più arretrato del previsto, rendendo il modello ancora più stabile di quanto si potesse supporre. Questo significa inoltre che a volte sono in grado di volare anche modelli in cui il baricentro e il centro delle aree laterali sono dati come coincidenti o addirittura come sistemati in maniera tale da causare un comportamento instabile; a puro titolo di esempio, il modello Dirty Bird III appartiene alla categoria di razzi che l'uso del metodo dell'area laterale classificherebbe come instabili e che invece sono in grado di volare benissimo.
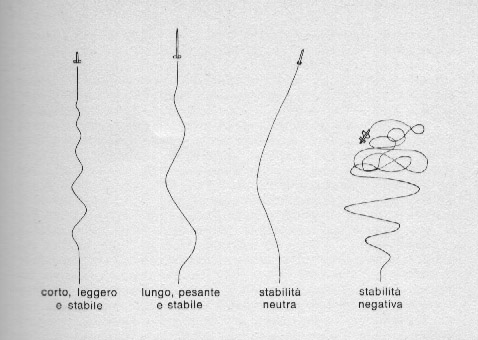
Fig. 55. Traiettorie di vari tipi di modelli.
Infine, a meno che non abbiate già una notevole esperienza alle spalle, usate il metodo dell'area laterale. E' semplice e attendibile, in poche parole " funziona ".
Nel 1966 Jim Barrowman, partendo da alcuni cenni trovati nei rapporti della NASA e della NACA, ha sviluppato una tecnica per calcolare l'effettiva posizione del centro delle pressioni: si tratta di un metodo che procede per gradi, suddividendo in tante parti ideali e che attualmente richiede circa 30 fasi di calcolo per il caso più semplice di un modello a un solo stadio. Barrowman è stato così in grado di precisare che il CP trovato con il metodo delle aree laterali è effettivamente quello che corrisponde a un volo piatto - con un angolo di attacco di 90° - e che il CP si sposta indietro al diminuire dell'angolo. E' stata così data conferma che il metodo delle aree laterali è conservativo e che è possibile far volare modelli che alla luce di questo metodo sembrano neutralmente stabili. Questo splendido lavoro di un modellista rende anche ragione del perché il Dirty Bird III si comporta molto bene per quanto apparentemente instabile.
Quali sono i rimedi da adottare se il modello sembra presentarsi in fase di progetto come neutralmente stabile o instabile? In genere non conviene fidarsi del fatto che i calcoli possono fornire risultati pessimistici, come già visto; ma è meglio ritoccare il modello per tentare di sistemare i due centri nella giusta reciproca posizione. Le correzioni più opportune dipendono naturalmente da caso a caso. E' possibile aumentare l'area o il numero delle pinne, ottenendo un aumento di resistenza e quindi uno spostamento indietro del centro delle pressioni; se invece il modellista non è disposto a questa soluzione, perché ad esempio ha in mano il modello di un missile vero in scala, di cui vuole mantenere intatte la forma e le dimensioni, allora può appesantire il modello sul davanti sistemando alcuni pesi sulla base dell'ogiva.
E' importante ora esaminare più a fondo il problema della stabilità; finora ci siamo soffermati a discutere le condizioni che rendono possibile un volo corretto e abbiamo visto quale deve essere la posizione relativa dei due centri affinché sia ottenuto lo scopo desiderato. Ora domandiamoci: sappiamo che il centro delle pressioni deve stare dietro al baricentro, ma a quale distanza? Questo problema è oggetto continuo di discussioni anche accese ed è ben lontano da una soluzione definitiva; l'autore si serve di una regola empirica che non l'ha mai tradito e che è semplicissima: la distanza fra i due centri deve essere pari a circa un diametro del corpo. Una distanza maggiore esaspera l'effetto timone delle pinne e introduce un controllo troppo energico, per cui il modello oscilla a ogni minimo soffio di vento; con un progetto accurato si può fare in modo di rendere questa distanza ancora minore, a tutto vantaggio di una perfetta linea di volo anche in condizioni di tempo ventoso.
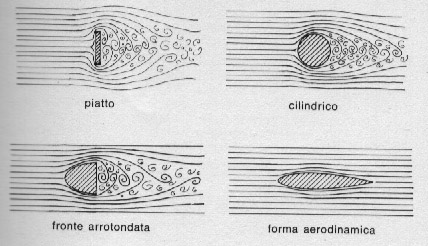
Fig. 56. Flusso di aria attorno a oggetti di varia forma.
I problemi connessi con la stabilità sono tanto numerosi che restano tuttora in gran parte senza soluzione; per chi abbia voglia di studiare e di dedicarsi a qualcosa di proficuo, questo è un campo meraviglioso, in cui occorrono però notevoli capacità matematiche e un'ottima conoscenza delle leggi fisiche. I rapporti degli enti spaziali e i libri di aerodinamica sono pieni di equazioni e di formule complesse, che il modellista non è quasi mai in grado di capire o applicare: intendiamo con questo dire che un lavoro di tal genere è per specialisti, e non per gente dotata solo di una leggera infarinatura.
Un altro fattore molto importante ai fini della stabilità è il " momento d'inerzia " (da non confondere con il metodo del momento utilizzato per il calcolo del centro delle pressioni), che ora cercheremo di illustrare affinché i modellisti possano rendersi conto di alcuni aspetti del volo (generalmente ignoti ai più, mentre meriterebbero maggior approfondimento e attenzione). I fatti sono questi: un modello lungo e affusolato comporta un volo caratterizzato da sbandamenti rapidamente corretti e smorzati, mentre uno corto e tozzo generalmente oscilla con maggior frequenza, sbandando soprattutto in corrispondenza del motore. La spiegazione sta nei differenti momenti di inerzia dei due modelli che provocano un diverso comportamento per quanto riguarda lo smorzamento aerodinamico di disturbi.
Ritorniamo ora alla nostra semplice " camera a vento " e al nostro bastone sperimentale. Mediante il solito cartoncino costruiamo le pinne in modo che il centro delle pressioni disti dal baricentro circa un diametro, cosi da realizzare quella situazione che l'autore ritiene ottimale ai fini della stabilità. Accendiamo il ventilatore e proviamo a disturbare il sistema spostando il bastone con le dita dalla sua posizione - che possiamo dire di riposo - per lasciarlo poi immediatamente libero. Sotto la spinta dell'aria il bastone tende a ritornare nella posizione precedente - ovvero puntato verso il flusso d'aria -, ma a causa della velocità rotazionale che acquista, la oltrepassa in genere senza arrestarvisi. Così il fenomeno riprende dalla parte opposta: il bastone " torna indietro " entrando in oscillazione e si ha uno smorzamento progressivo sino ad arrivare di nuovo in condizioni di equilibrio. Un modello lungo e affusolato ha l'ogiva e il motore - che in pratica sono le parti più pesanti - molto distanti fra loro e dal baricentro: questo comporta che l'effetto stabilizzatore dovuto alla spinta dell'aria introduce basse accelerazioni rotazionali delle masse suddette intorno al baricentro le oscillazioni del modello sono pertanto lente e si smorzano molto rapidamente dopo solo pochi passaggi sulla posizione di riposo. In questo modo si ha un ottimo controllo, dovuto al fatto che grande è il momento di inerzia.
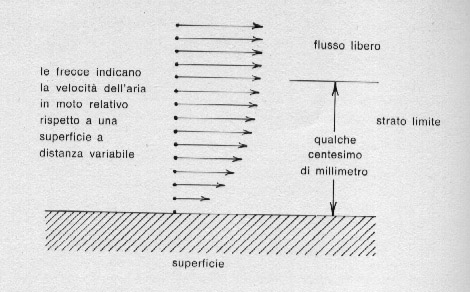
Fig. 57. Strato limite.
Invece un modello corto oscilla molto rapidamente attorno al suo baricentro, passando ripetutamente sulla posizione normale di volo; la causa di ciò è un momento di inerzia tanto piccolo che anche i minimi disturbi vengono sentiti senza essere sufficientemente smorzati. Un modello di questo tipo richiede necessariamente l'uso di pinne stabilizzatrici enormi.
Gli effetti che la forma delle pinne, il rapporto lunghezza-diametro, e il momento di inerzia introducono nella stabilità e nello smorzamento delle oscillazioni non possono essere oggetto di studio in questa sede e sono in genere trascurati dai modellisti. Del resto c'è da dire che non è semplice studiare questi fenomeni perché coinvolgono nozioni e metodi di calcolo che solo poche persone esperte sono in grado di affrontare. A ben pensarci, per tutta la precedente trattazione ci siamo serviti solo della statica mentre sarebbe stato necessario anche l'uso della dinamica.
Abbiamo preferito seguire questa strada per semplificare la esposizione della teoria, ma ci siamo messi in condizioni di non poter descrivere proprio tutto, in quanto la statica è per il nostro problema uno strumento inadeguato. La relazione fra i due centri ci fornisce senz'altro indicazioni precise sulla stabilità del sistema ma è inefficace a determinare gli effetti dinamici e a dare una risposta ai seguenti quesiti: quale deve essere l'intensità della forza per girare il modello di un angolo prestabilito; con quale velocità il modello ruota e oscilla; quanto rapidamente il disturbo si smorza.
Il lettore ha avuto modo di toccare con mano che fare il modellista di razzi può diventare molto complesso, perché si ha a che fare con un corpo libero nello spazio e pertanto dotato di un moto complicato anche se affascinante. Questa problematica generalmente sfugge all'amatore, mentre è continuo oggetto di studio da parte del vero modellista. I problemi della stabilità nel volo concernono sia i grandi che i piccoli modelli, ma è più agevole compiere delle misurazioni sui grandi. Per contro, i piccoli modelli sono più " sicuri ", molto meno costosi e di più facile sperimentazione in questo particolare campo.
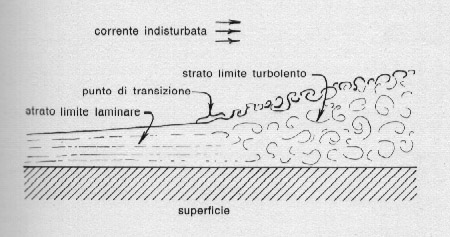
Fig. 58. Transizione dello strato limite dell'aria da strato laminare a strato turbolento.
Per ottenere un buon comportamento aerodinamico è necessario dare al missile e alle sue parti forme opportune: questo argomento si è dimostrato via via piú importante e cercheremo di studiarlo a fondo.
Molti anni fa i primi costruttori di aerei si accorsero di poter limitare la resistenza dell'aria sagomando opportunamente le loro costruzioni: da queste prime osservazioni si è poi sviluppata una tecnica speciale per capire la sagoma migliore per un corpo veloce, tecnica che oggi è applicata correntemente in molti campi, gare automobilistiche incluse. In verità una lastra piana che si muova perpendicolarmente alla sua superficie incontra una forte resistenza; a tutti è noto che se si mette una mano fuori del finestrino di una macchina lanciata a 100 km/h la si sente sollecitata da una grossa spinta all'indietro, mentre la spinta diminuisce notevolmente se si chiude a pugno la mano.
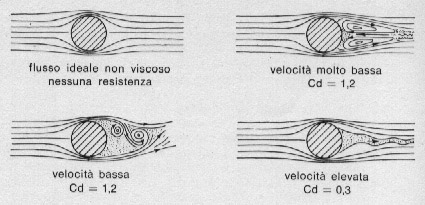
Fig. 59. Flusso d'aria attorno a un cilindro sotto diverse condizioni.
Il fenomeno è spiegabile osservando che l'oggetto in movimento deve allontanare l'aria che incontra nella sua traiettoria e che la scia formata deve poi richiuderglisi alle spalle. La forma in movimento ha perciò un'importanza fondamentale per definire il tipo di moto che l'aria assume e al quale è correlata strettamente la resistenza che ne deriva. La fig. 56 riporta alcune situazioni tipiche.
La forma di un oggetto e il cammino dell'aria hanno quindi un enorme effetto sulla resistenza che, per chiarezza, possiamo scomporre in diverse parti a) resistenza dovuta all'attrito; b) resistenza dovuta alla pressione; c) resistenza per interferenza; d) resistenza parassita; e) resistenza dovuta alle forze trasversali.
Per visualizzare il fenomeno possiamo schematizzare l'aria come un corpo formato da tante particelle microscopiche, dette molecole, così piccole da essere invisibili anche al microscopio: un cm^3 di aria ne contiene qualcosa come 30 miliardi di miliardi. Quando queste minuscole palle da ping-pong scivolano su una pinna o sul corpo generano una resistenza dovuta all'attrito (a), e rendono ragione del fatto che tale forme di resistenza dipende dalla levigatezza della superficie; al crescere della rugosità incontrano difatti maggiore difficoltà a scorrere via, così come è facile scivolare su un pavimento di marmo tirato a cera mentre è impossibile su un selciato.
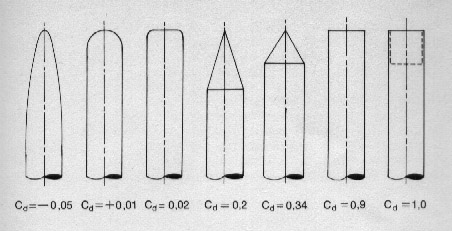
Fig. 60. Coefficiente di resistenza per varie forme di ogiva.
La corrente d'aria in vicinanza dell'oggetto in moto presenta strane particolarità: le molecole direttamente a contatto restano ferme, perché lo sforzo d'attrito è tanto grande da arrestarle; quelle che si trovano a strati superiori si muovono via via più velocemente fino a restaurare la velocità indisturbata, a sufficiente distanza secondo il disegno della fig. 57. Questo flusso in vicinanza della superficie viene chiamato " strato limite " ed esiste sempre quando un corpo si muove in aria; il suo spessore, tenendo conto che le molecole devono slittare l'una sull'altra come nella fig. 57, varia con le forme del modello e la velocità dell'aria; come ordine di grandezza si può dire che per un piccolo razzo del diametro di 2 cm e lungo 20 cm lo strato limite è spesso di 25 micron o poco più
Lo strato limite può essere laminare o turbolento, come mostra la fig. 58. Quando si passa in regime turbolento, gli strati molecolari non scivolano più ordinatamente l'uno sull'altro, ma si muovono in modo disordinato formando continuamente vortici; di conseguenza lo strato limite aumenta di spessore, restando sempre attaccato alla superficie che lo provoca.
Il passaggio da laminare a turbolento avviene anche su corpi molto levigati a una distanza sufficiente dal capo dell'oggetto: questa distanza dipende da dimensioni, forma, grado di rifinitura e velocità del modello. Va messo in evidenza che la resistenza di attrito dovuta a uno strato limite turbolento è più alta di quella causata da uno laminare.
Il passaggio a regime turbolento può essere causato anche da una piccolissima irregolarità della superficie, come potrebbe essere per una gibbosità di soli 7-8 micron: si capisce quindi l'importanza di rifinire bene con carta vetrata finissima allo scopo di stabilizzare lo strato limite laminare per quanto possibile.
La resistenza dovuta alla pressione (b) è causata dall'urto diretto delle molecole contro la superficie: sul capo di un oggetto in moto dentro un fluido è ovvio che la pressione assuma un valore maggiore di quello che si ha in tutto il resto del campo. E' possibile anche avere una resistenza negativa allorché la pressione nello strato limite si abbassa al di sotto del valore assunto nell'aria libera.
Se non ci fosse strato limite e l'aria non fosse viscosa, non si manifesterebbe nessuna resistenza: come nel primo schizzo di fig. 59, l'aria si sposterebbe al passaggio dell'oggetto e poi gli si chiuderebbe dietro senza alcuna conseguenza. Un comportamento di questo tipo è puramente ideale, ma si può presumere che si comportino così corpi piccoli, quali sono le gocce di pioggia che si muovono nell'aria a velocità estremamente basse.
Al contrario, un corpo delle dimensioni di un modello non dà all'aria il tempo necessario per scansarsi e richiudersi in maniera ordinata, anche a causa della elevata velocità; in altre parole lo strato limite si rompe creando alle spalle del razzo un campo di moto turbolento e ricco di vortici. Questa situazione non va confusa con lo strato limite turbolento perché quest'ultimo aderisce al corpo, mentre nel nostro caso siamo in presenza di una scia che il modello si tira dietro.
La fig. 59 mostra un cilindro che si muove nell'aria a varie velocità e mette in evidenza il tipo di flusso che l'aria assume.
E' possibile ridurre sensibilmente la resistenza in questione sagomando in maniera opportuna la parte anteriore dell'oggetto in modo da rendere minima la pressione dovuta all'impatto con le molecole dell'aria. A questo scopo sono state effettuate molte prove in camera a vento, sia in America sia in Germania: questa lunga serie di studi ha permesso di precisare il comportamento dei vari tipi di ogiva (fig. 60) e di trovare la forma che offre migliori garanzie di buon comportamento. Si può dire che la forma arrotondata - meglio se parabolica - rappresenta per un modellista il " non plus ultra ".
Di fronte a una tale affermazione i modellisti si mostrano spesso scettici perché non riescono a spiegarsi il motivo per cui i razzi veri sono tutti affusolati e appuntiti, invece di avere ogive di questo tipo. Dal loro punto di vista la difficoltà di adottare soluzioni come quella da noi consigliata consiste nel fatto che, così, i loro modelli acquistano un aspetto che imita poco la realtà. Ebbene, il modellista dubbioso deve capire che fra la sua creazione e il missile vero esiste una differenza sostanziale, che cioè questo è progettato per volare a velocità supersoniche mentre il suo raramente supera i 150-200 km/h. Questo fatto rende ragione del diverso tipo di ogiva da impiegare e di perché il campo di moto che si crea è notevolmente diverso nei due casi. Le considerazioni che abbiamo fatto e le forme che abbiamo consigliato sono quelle che vanno bene nel moto sub-sonico.
A sostegno di quanto detto invitiamo coloro che ancora fossero dubbiosi a dare uno sguardo a uno degli aerei subsonici che ci sono in circolazione - come il Boeing 707 - per verificare come effettivamente abbiano una punta arrotondata.
La forma migliore da dare a un'ogiva appare la parabolica, così come è messo in evidenza nella fig. 60, ma sorge subito il problema di dimensionarla. Successivi esperimenti con la camera a vento hanno mostrato che il relativo coefficiente di resistenza Cd è una funzione del rapporto lunghezza-diametro, come appare in fig. 61; perciò la lunghezza da assegnare a un'ogiva di questo tipo è dell'ordine di 3-4 volte il diametro della sua base; farla più corta danneggia l'aerodinamicità, allungarla ulteriormente non serve a niente. A titolo di esempio l'ogiva migliore per un razzo con un corpo del diametro di 2 cm si aggira sui 6-8 cm.
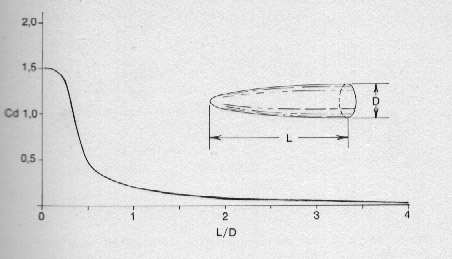
Fig. 61. Coefficiente di resistenza di un'ogiva parabolica in funzione del rapporto lunghezza-diametro.
Per semplicità a volte si montano anche ogive squadrate, che però sono disastrose ai fini dell'aerodinamicità; il nostro consiglio è di smussare almeno gli angoli con un po' di carta vetrata nel tentativo di migliorarne l'efficienza, perché sui razzi anche una precauzione di questo genere può ottenere sensibili miglioramenti.
In coda al modello si sviluppa una grande resistenza causata dal distacco dello strato limite e dalla scia turbolenta sempre presente: contro un tale tipo di inconveniente il modellista è praticamente impotente, per quanto con un po' di esperienza riesca a trovare soluzioni soddisfacenti.
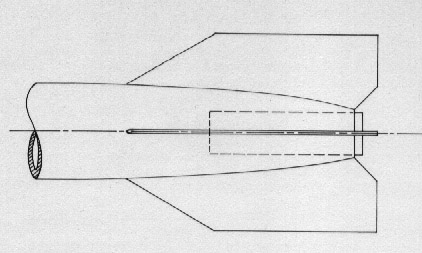
Fig. 62. Forma da dare alla parte posteriore del corpo del razzo per ridurre la resistenza.
Poiché il diametro di un modello non è molto più grande del motore usato, il razzo si trascina sempre dietro una scia turbolenta una volta che il propellente è esaurito. Durante il volo di spinta il motore stesso genera una quantità enorme di gas, aumentando così la turbolenza in coda e, con essa, la resistenza; invece quando brucia " in ritardo " si generano solo piccoli quantitativi di gas, che rendono la pressione in coda al motore debolmente positiva, cosicché la resistenza risulta notevolmente ridotta. Tutto l'argomento non ha ricevuto finora l'attenzione che merita e gli esperimenti compiuti sono pochi.
I modellisti che usano corpi più grandi del contenitore del motore allo scopo di sollevare pesi o imitare meglio la forma dei missili veri, sentono la necessità di limitare la resistenza dovuta alla turbolenza dell'aria in coda. Ricorrono così alla soluzione dì fig. 62, rastremando la coda in una forma elegante e aerodinamica. Per dimensionare opportunamente una coda di questo genere occorre affidarsi all'intuito e all'esperienza perché mancano completamente dati sperimentali; a titolo di consiglio, e per quanto non ci siano possibilità di confermare quanto segue, l'autore suggerisce di non eccedere troppo - pena il rischio di distaccare lo strato limite o di renderlo turbolento - e di cominciare il restringimento a una distanza dalla coda pari a 3-4 diametri. Un'altra soluzione può anche essere rappresentata dalla forma a tronco di cono, ricavata da un tubo di carta o da balsa lavorata al tornio e scavata internamente.
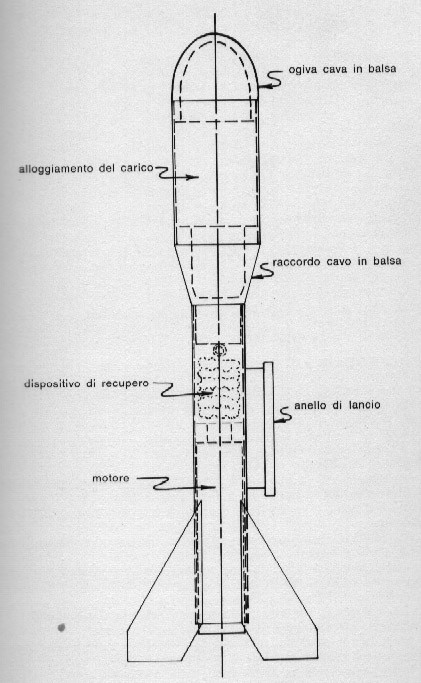
Fig. 63. Modello costruito per trasportare grandi carichi: notare il raccordo fra le due parti a sezioni diverse.
I modellisti a volte usano costruire i loro razzi secondo il disegno di fig. 63, con la parte anteriore tanto larga da poter contenere oggetti di varia natura e quella posteriore dimensionata sul diametro del motore: in questo caso è importante curare la forma dell'ogiva e raccordare dolcemente le due parti di diverso diametro.
Dalla discussione precedente risulta abbastanza evidente che anche le pinne devono aver un profilo aerodinamico, e ci sembra superfluo spiegare che devono essere arrotondate nella parte anteriore e rastremate in quella posteriore, allo scopo di offrire la minima resistenza possibile al flusso dell'aria
La resistenza per interferenza (c) è causata dal flusso di aria, disturbato fra due oggetti o da due superfici piane intersecate fra loro. In un modello, effetti di questo tipo sono presenti alla giunzione ad angolo retto delle pinne con il corpo e spiegano come la soluzione con tre pinne invece che quattro è preferibile per il solo fatto che riduce l'interferenza di circa il 25 %. Per eliminare questa sorgente di dissipazione si può raddolcire la giunzione con un leggero filetto di colla, senza però esagerare perché altrimenti la resistenza dovuta all'attrito, con l'aumento della superficie, comincia a farsi sentire tanto da annullare il miglioramento ottenuto.
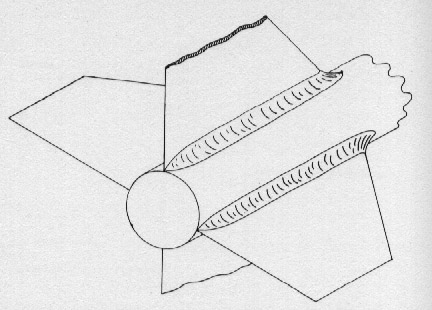
Fig. 64. Filetti di colla per ridurre la resistenza per interferenza.
La resistenza parassita (d) è causata da strutture poco aerodinamiche come gli anelli di lancio o le protuberanze in scala introdotte allo scopo di realizzare modelli perfetti. E' vero che quasi mai si arriva a valori notevoli, ma quando sì cerca di ottenere il massimo rendimento è meglio considerare l'opportunità di eliminare tutte le parti di resistenza parassite, minimizzando ad esempio l'anello di lancio o facendo ricorso a una vera torre.
La resistenza dovuta a forze trasversali (e) si manifesta quando alcune parti del modello presentano un angolo di attacco. Questa possibilità esiste soprattutto in corrispondenza delle pinne, le quali (fig. 65) generano una forza resistente ogni volta che sono chiamate a esercitare la loro funzione stabilizzatrice. Tutto questo è messo molto bene in evidenza nella figura: a causa del moto, fra pinna e aria si crea una forza - che tende a riportare il modello nelle esatte condizioni di volo - suscettibile di essere scomposta in una parte verticale veramente efficace a questo scopo e in un'altra orizzontale che assume le vesti di una resistenza.
Spinte trasversali di questo tipo sono usate negli aerei, e spiegano perché le ali sono effettivamente in grado di sostenere il velivolo.
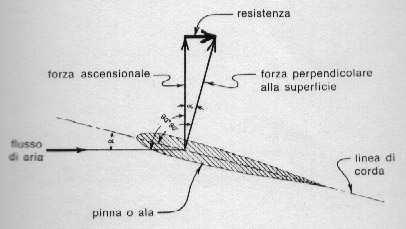
Fig. 65. resistenza dovuta alle forze trasversali.
Un'ala genera una forza di sostentamento a causa della sua forma particolare; come abbiamo là avuto modo E vedere il suo profilo non è simmetrico, ma leggermente convesso nella parte superiore: di conseguenza l'aria che passa al di sopra dell'ala deve compiere un cammino maggiore ed è perciò dotata di una velocità più elevata, il che riduce la pressione.
Una sorgente importante di resistenza è localizzata alla estremità delle pinne, quando il volo avviene con un angolo di attacco. In queste condizioni si ha un effetto stabilizzatore e le pinne si presentano inclinate al flusso dell'aria: il loro profilo è come se fosse asimmetrico e si genera pertanto una fenomenologia come quella che si manifesta sulle ali.
Tra le due facce c'è un dislivello di pressione, per cui al bordo l'aria si muove verso la parte a pressione minore (fig. 66); il risultato è un flusso a spirale, conosciuto come vortice, che introduce una resistenza aggiuntiva nota come " resistenza indotta ". Per eliminare o almeno ridurre questo inconveniente si può aggiungere al bordo della pinna ostacoli al flusso di aria - che però comportano una indesiderata resistenza, aggiuntiva, di interferenza - oppure si dà alla pinna una sagoma opportuna. Questa ultima soluzione è la più diffusa (fig. 67): una forma abbastanza buona da questo punto di vista è la quadrata, ma forse si comportano meglio sagome ellittiche, mentre non si può affermare lo stesso per quelle arrotondate.
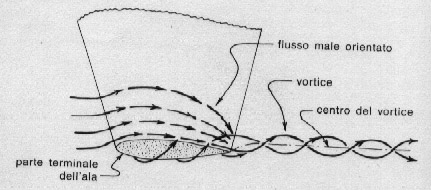
Fig. 66. generazione di vortici al bordo di un'ala o di una pinna con formazione di resistenza indotta.
La resistenza rappresenta forse la difficoltà maggiore che i modellisti devono superare: il suo effetto è tanto rilevante da compromettere a volte un progetto apparentemente buono ed esteticamente gradevole. Non bisogna mai dimenticare che a volte è preferibile abbandonare la perfetta imitazione di un missile vero per avvicinarsi a soluzioni più efficienti e redditizie; sappiamo che il perfetto missile in scala è una cosa affascinante, ma vogliamo far presente che il vero modellista - almeno come lo intendiamo noi - non si limita a guardare il modello, compiaciuto della sua forma, ma vuole che voli bene e alto.
Perciò i problemi di resistenza prima o poi si faranno sentire, fino a diventare il fulcro di tutta l'attività e l'elemento ispiratore di qualunque progetto. Su questo tema in genere si accendono discussioni calorosissime e si sviluppa uno spirito di emulazione notevole: in effetti l'argomento appare molto interessante e praticamente senza fine, tanto che nemmeno ì professionisti sono ancora riusciti a sviscerarlo del tutto.
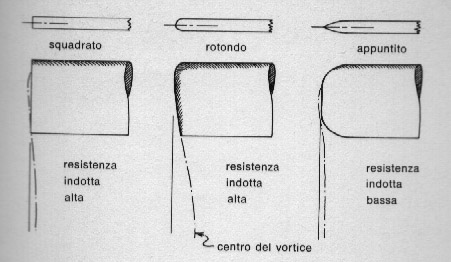
Fig. 67. resistenza indotta su tre tipici profili di pinna.
Con un po' di pratica ognuno riesce a sviluppare e adottare soluzioni sue personali alle quali generalmente resta fedele: questo è un bene perché è sintomo di una ricerca che sembra approdata a qualcosa di buono; ma non bisogna accontentarsi tanto da dimenticare che vale la pena cercare sempre migliori soluzioni.