CAPITOLO V
Modelli in volo
Una volta che si è alzato e si è allontanato dalla superficie terrestre, il modello è un corpo libero nello spazio il cui comportamento non può essere simulato facendo esperimenti su corpi vincolati al suolo. In volo le forze sono abbastanza diverse da quelle che si hanno quaggiù; il modello può essere considerato veramente un corpo spaziale perché, trascurando alcuni effetti secondari dovuti all'atmosfera e di cui si può facilmente tener conto, tutto si svolge come se si trovasse a 3000 km di altezza.
Il volo di un modello consiste in tre fasi: il volo per effetto della spinta del motore, quello per inerzia e il rientro; in questo capitolo prenderemo in considerazione solo le prime due fasi, Mentre l'ultima sarà oggetto di studio in un prossimo capitolo.
La prima fase, che possiamo definire " di spinta ", è di breve durata, ma sufficiente per imprimere al modello una velocità tale da permettergli di raggiungere altezze considerevoli nella seconda. Queste due prime fasi sono abbastanza diverse fra loro perché diverse sono le forze in gioco: l'una vede l'azione contemporanea della spinta dovuta al motore, della resistenza dell'aria e della gravità terrestre, mentre l'altra si svolge sotto l'effetto delle sole forze aerodinamiche e gravitazionali.
E' impossibile descrivere correttamente il comportamento di un oggetto volante senza usare un po' di matematica che, nel nostro caso, è limitata a poche, basilari nozioni; per capire quindi il fenomeno in studio ci soffermiamo un attimo a richiamare gli aspetti fondamentali della teoria del moto, così come è descritta nei libri di fisica.
Quando, un corpo è in movimento e va da un punto A a un punto B, si dice che copre la distanza X tra A e B: nel nostro schema semplificato noi supponiamo che tale distanza venga percorsa con moto rettilineo. Se il tempo impiegato è 1 sec e la distanza è 1 m, allora si dice che il corpo si muove con una velocità di 1 metro al secondo (1 m/sec); in generale se X è lo spazio percorso e T il tempo necessario, la velocità si ottiene dividendo la distanza per il tempo: V = X/T. Se la velocità è costante anche il moto lo è e ne deriva che in tempi uguali il mobile percorre spazi uguali.
Se la velocità non si mantiene costante, ma è soggetta a variazioni, il corpo è accelerato. Può darsi che la variazione di velocità sia costante; se al tempo T1 il corpo si muove con una velocità di 1 m/sec e al tempo T2 con una velocità di 2 m/sec, si dice che la variazione di velocità nell'intervallo di tempo considerato è stata di 1 m/sec; se poi l'intervallo è di 1 sec, si dice che la variazione di velocità per unità di tempo o accelerazione, è stata di 1 m/sec^2.
In modo analogo anche l'accelerazione può non essere, costante: se varia di 1 m/sec^2 in un secondo, allora la sua variazione nell'unità di tempo è di 1 m/sec^3.
Nel 1687 un teologo e astrologo, Isacco Newton, pubblicò un trattato intitolato Philosophiae Naturalis Principia Matematica, in cui proponeva tre semplici leggi per descrivere il moto dei corpi, tuttora considerate valide. Esse sono:
1) Legge d'inerzia: un corpo fermo rimarrà fermo; un corpo in movimento continuerà a muoversi di moto rettilineo uniforme, se non è sottoposto a nessuna forza esterna.
2) Legge dell'accelerazione: le variazioni di moto di un corpo sono proporzionali all'intensità della forza agente e avvengono nella direzione in cui la forza agisce.
3) Legge di reazione: a ogni azione corrisponde una reazione uguale e contraria.

Un modello in volo ubbidisce a tutt'e tre queste leggi: per esempio, il motore produce la spinta in virtù della terza legge e il volo è regolato dal complesso delle prime due.
La seconda legge espressa in forma matematica assume questa forma:
F = ma (1)
dove F = forza applicata, m = massa del corpo e a = accelerazione risultante; se raddoppia la forza, e se la massa si mantiene costante, anche l'accelerazione raddoppia mentre, a parità di forza, l'accelerazione decresce se la massa aumenta.
In qualsiasi libro di fisica si può trovare lo sviluppo delle equazioni seguenti, cosicché noi ci limitiamo semplicemente a elencarle e a mostrarne poi l'uso in un caso pratico:
s = vt (2)
vm=(v1+v2)/2 (3)
a=(v2-v1)/t (4)
s=v1t+(at^2/2) (5)
2as = v2^2 - v1^2 (6)
dove s = distanza, v = velocità, v1 = velocità al tempo zero, v2 = velocità dopo un tempo t, vm = velocità media, a = accelerazione e t = intervallo di tempo.
Il modo migliore per spiegare l'uso di queste equazioni è applicarle a un caso concreto e calcolare cosi effettivamente il comportamento di un modello reale. Supponiamo perciò di voler descrivere la traiettoria e il volo di un razzo che presenti le seguenti caratteristiche:
massa al momento del lancio m1= 43 g
massa quando il motore si spegne m2=37 g
spinta media del motore F=4 Nw
durata del motore t = 1,5 sec
Potremmo calcolare l'accelerazione applicando l'equazione (4) della seconda legge, ma a titolo di esercizio lasciamo al lettore il compito di tradurla nella forma seguente:
Ao= (F-P)/m1 (7)
Sostituendo i valori numerici opportuni, otteniamo l'accelerazione al momento della partenza:
Ao= (4-9,8(0.043))/0,043 = 4/0,043-9,8 = 83,3 m/sec^2
Poiché il motore brucia e consuma propellente, il modello diventa via via più leggero man mano che sale: la sua massa perciò cambia e l'accelerazione cresce. Usando di nuovo l'equazione (1) possiamo perciò calcolare l'accelerazione al momento in cui il motore si spegne, sostituendo il giusto valore della massa a tale istante.
A1=(4-9,8(0,037)) / 0,037 = 4 / 0,037-9,8 = 98,3 m/sec^2
Si scopre quindi che l'accelerazione non si è mantenuta costante, ma per tener conto di questo fatto in modo rigoroso occorrono metodi matematici più raffinati della semplice algebra; è possibile però effettuare un calcolo sufficientemente preciso utilizzando il valore medio dell'accelerazione nell'intervallo di tempo considerato:
Am= (Ao+A1) / 2 = (83,3 + 98,3) / 2 = 90,8 m/sec^2
La velocità al momento in cui si spegne il motore, e che coincide con la massima velocità raggiunta dal modello, è calcolabile con l'equazione (4), dove vi è posta uguale a zero per tener conto del fatto che al momento del lancio il razzo è fermo:
Vmax= Amt = 90,8 (1,5) = 136,20 m/sec (9)
La velocità media durante la fase " di spinta " è ottenibile dall'equazione (3):
Vm= (136,2 + 0) / 2 = 68,1 m/sec
Usando l'equazione (2) possiamo adesso calcolare l'altezza massima raggiunta in questa fase dal modello:
s1 = 68,1 (1,5) = 102,15 m
oppure possiamo fare uso dell'equazione (5):
s1 = at^2 / 2 = 90,8 (1,5)^2 / 2 = 102,15 m
che fornisce esattamente lo stesso risultato.
Possiamo quindi concludere che, alla fine di questa prima fase, il modello ha raggiunto una quota di 102,15 m e si muove con una velocità di 136,20 m/sec, che corrisponde a circa 490,32 km/h: trattandosi di un piccolo modello, il risultato ottenuto è senz'altro notevole!
E' anche possibile calcolare la velocità al momento in cui il motore si spegne, conoscendo l'impulso totale del motore e il peso del modello a tale istante. Difatti l'impulso totale rappresenta per definizione la variazione di quantità di moto mv, cosicché possiamo scrivere:
It = m1V1 - movo (10)
e poiché al tempo zero la velocità è nulla, l'equazione si riduce a
It = m1V1
da cui è possibile ricavare la velocità:
V1 = Vmax = It / m1
Esprimendo l'impulso totale come prodotto della spinta media e della durata, e ricordando che al momento considerato la massa del modello è di 37 g, è facile effettuare i passaggi seguenti:
Vmax = Ft / m2 = 4 (1,5) / 0,037 = 162 m/sec
ottenendo un risultato che si accorda abbastanza bene con quanto ottenuto precedentemente; a titolo, di commento, c'è da dire che il metodo dell'impulso totale è semmai più accurato, poiché la spinta del motore non è affatto costante.
Quando la spinta del motore si è esaurita, il modello si sta muovendo con una velocità considerevole, ma è ancora a un'altezza relativamente bassa; il ritardo introdotto nel funzionamento del dispositivo di recupero serve proprio a fare in modo che possa
raggiungere per inerzia altezze maggiori prima di cominciare la discesa. Per quanto in questa fase siano presenti solo le forze gravitazionali e aerodinamiche, per il momento trascureremo queste ultime e descriveremo il modello come un corpo che si muove liberamente sotto l'effetto del proprio peso e per questo soggetto a una accelerazione verso il basso di 9,8 m/sec^2. Poiché abbiamo già calcolato la velocità Vmax, possiamo usare l'equazione (6) per determinare il dislivello che il modello supera in questa seconda fase:
s2= Vmax^2 / 2g = (162)^2 / 2 (9,8) = 1340 m
L'altezza massima raggiunta è ovviamente la somma delle due altezze parziali già calcolate:
S = s1+ s2 = 102,15 + 1340 = 1442,15 m
Soffermiamoci ora un po' a osservare le equazioni usate e i calcoli fatti, perché ci sono alcune osservazioni importanti da fare.
Se costruiamo, un modello più leggero l'accelerazione è più alta e di conseguenza è maggiore la velocità quando si spegne il motore.
Se raddoppiamo la durata della spinta del motore, l'altezza raggiunta alla fine del volo " di spinta " aumenta quattro volte.
Se raddoppiamo la velocità alla fine della prima fase " di spinta ", il dislivello superato nel volo per inerzia si quadruplica.
Lo, studio condotto fin qui, per quanto lungo, è abbastanza semplice e permette di avere le idee un po' più chiare sul fenomeno che stiamo studiando. Abbiamo, per esempio, imparato che i parametri più importanti sono quelli che compaiono sotto forma di quadrati e siamo in grado di dire, senza entrare nei particolari di una discussione noiosa e ancora più lunga, che i fattori predominanti sono l'impulso totale, il peso alla fine della prima fase e la durata del motore. La spinta iniziale del motore determina solo l'accelerazione iniziale che, a sua volta, influenza la velocità con cui il modello lascia la rampa di lancio: da questa dipende quindi la lunghezza dell'asta da usare.
Ci proponiamo ora di guardare il problema da un altro punto di vista, perché in tutta la trattazione precedente è stato completamente ignorato il fatto che il modello vola nell'atmosfera terrestre ed è pertanto soggetto a una forza resistente che si oppone alla spinta del motore, rallentando e abbreviando il volo nella fase per inerzia. Questa resistenza può assumere anche valori notevoli.
Le precedenti equazioni possono perciò essere considerate un caso limite, in quanto descrivono il miglior comportamento possibile del modello sotto condizioni ideali; quando si comincia a tener conto anche delle forze aerodinamiche, il calcolo non è più cosi semplice e diventa lungo e laborioso.
La resistenza che un corpo incontra muovendosi in un fluido come l'aria dipende dalla sua forma, dalle sue dimensioni, dalla sua velocità, dalla temperatura dell'aria e dalla pressione atmosferica; dipende, in misura minore, anche dallo stato di levigatezza delle superfici.
Il solo metodo per determinare accuratamente la resistenza aerodinamica consiste nel riprodurre in un tunnel a vento esattamente le condizioni di volo: pochi modellisti hanno però libero accesso ad apparecchiature del genere, e pochissimi sono in grado di usarle. Alcuni hanno tentato di costruirsene una, ma si sono messi su una strada difficile e dispendiosa, ottenendo quasi sempre risultati mediocri perché la loro camera in genere non imita bene il comportamento in volo a causa di una elevata turbolenza dell'aria
L'unica cosa che resta da fare è arrangiarsi con risultati approssimativi, adottando al proprio caso formule e dati che gli esperti hanno ricavato sperimentalmente.
L'equazione di base per il calcolo della resistenza è di difficile dimostrazione e ha comunque questo aspetto:
R = 0,5 pv^2Cds (11)
dove R = forza resistente, p = densità dell'aria, v = velocità del modello, Cd = coefficiente adimensionale che dipende dalla forma del modello e s = area della superficie piana della sezione frontale del modello.
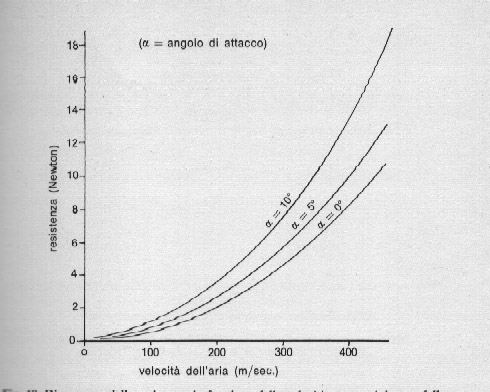
Fig. 48. Diagramma della resistenza in funzione della velocità per un tipico modello di razzi.
Soffermiamoci a considerare attentamente questa equazione per capire bene cosa vuol dire.
La resistenza dipende linearmente dalla densità dell'aria, decresce, quindi, se questa diminuisce: un aumento della quota o un aumento della temperatura dell'aria hanno proprio quest'effetto; per calcolarlo, è bene servirsi della Tab. 5.

La resistenza aumenta secondo il quadrato della velocità: se la velocità raddoppia, essa diventa quattro volte tanto. Ne deriva che, quanto più veloce va il modello tanto più la forza resistente si fa sentire; la fig. 48 riporta diagrammi tipici in funzione della velocità.
La resistenza aumenta linearmente con il coefficiente di resistenza, che assume valori estremamente variabili e può essere determinato solo con prove in tunnel a vento; d'altro canto Cd non dipende dalle dimensioni del modello, perché adimensionale, cosicché due ogive di uguale forma possono non essere caratterizzate dallo stesso valore Cd. Milioni di forme sono state sperimentate e ora sono noti i relativi coefficienti che anche i modellisti possono tranquillamente usare per i loro scopi.
Il coefficiente non è una costante, ma dipende dal cosiddetto " angolo d'attacco " (fig. 49), definito come quell'angolo formato dall'asse longitudinale del modello con la direzione del volo. Per le nostre forme esso aumenta al crescere dell'angolo, poiché l'area frontale che il modello presenta al flusso di aria cambia e aumenta all'aumentare dell'angolo. Poiché un modello che oscilla vola a vari angoli di attacco, la resistenza che incontra è maggiore che se volasse senza sbandamenti sicuro e diritto: questo è il motivo per cui è importante progettare un razzo dal volo lineare, se si vuole ottenere il migliore risultato.
Una dipendenza tipica di Cd dall'angolo è riportata in fig. 50, così come è stata ottenuta facendo esperimenti su un razzo Aerobee-Hi (lungo 30 cm, con corpo dal diametro di circa 2 cm e tre pinne stabilizzatrici), che può essere considerato ormai un classico.
La camera a vento è stata messa a disposizione dall'Accademia delle Forze Aeree degli Stati Uniti d'America, e la prova è stata fatta con una velocità dell'aria di circa 25 m/sec: i risultati ottenuti sono attendibili perché ricavati con apparecchiature e tecniche perfette.
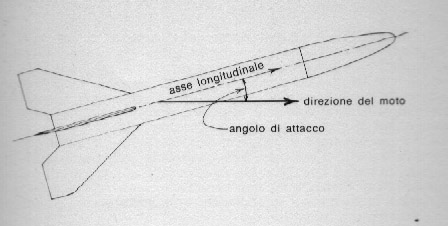
Fig. 49. Angolo di attacco.
Guardando ancora la formula del coefficiente di resistenza si vede che questo cresce con l'aumentare dell'area frontale; più precisamente se il diametro del corpo raddoppia, Cd diventa quattro volte più grande: ecco perché si costruiscono razzi e missili veri il più slanciati possibile, in modo tale che il corpo contenga giusto il motore.
Poiché la resistenza dell'aria agisce come una forza frenante, essa è quasi esattamente opposta alla spinta del motore se poi la traiettoria è verticale la sua azione è diretta come quella della forza di gravità, cui si somma letteralmente. Nell'equazione che fornisce l'accelerazione del missile si deve tener conto anche di questo, scrivendola nella forma seguente:
A = (F-R-P) / m = ((F-R) / m) - g (12)
Pur essendo in grado di calcolare con questa equazione il volo del modello, non bisogna però nascondere che la procedura è lunga e laboriosa perché la forza resistente non è assimilabile a una costante, a causa della sua forte dipendenza dalla velocità. D'altro canto è possibile separare idealmente il volo in tante fasi successive, ciascuna delle quali di durata piccolissima, in modo che la velocità vari poco all'interno di ognuna: cosi facendo R può essere ritenuta costante con discreta approssimazione e il calcolo effettivo procedere gradino per gradino.
Cominciando cioè dall'istante della partenza, in cui v = 0, si suppone che nel primo intervallo di tempo (fissato per esempio a 0,1 sec) v sia sempre prossimo a zero; allora R = 0 e la (12), insieme con le altre equazioni, permette di calcolare tutte le grandezze di interesse secondo lo schema già riportato. In particolare si ottiene un valore di velocità e uno di quota che servono come dati di ingresso per il secondo intervallo.
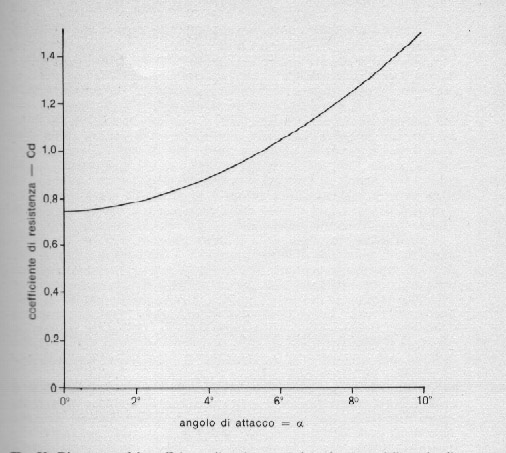
Fig. 50. Diagramma del coefficiente di resistenza Cd in funzione dell'angolo di attacco, per un tipico modello di razzi.
A questo modo è possibile descrivere via via tutto quanto accade durante il volo, ma il procedimento è chiaramente molto lungo; in realtà quando si tratta di missili veri, calcoli di questo genere sono affidati a un elaboratore elettronico che è capace di svolgerli in pochissimi secondi e che quindi si dimostra utilissimo e praticamente insostituibile.
Poiché un modello non vola sempre secondo la verticale, occorre tenerne conto, per essere in grado di effettuare i calcoli, specie se la partenza non avviene secondo la verticale: si arriva cosi alla seguente equazione:
A = ((F-0,5 p v^2 Cd s) / (m-m0)) -g (sen theta) (13)
dove: A = accelerazione nell'intervallo di tempo considerato, F = spinta del motore, p = densità dell'aria, v = velocità all'inizio dell'intervallo, Cd = coefficiente di resistenza ricavabile dai dati e dipendente dall'angolo di attacco, s = area della sezione trasversale del modello, m = massa all'inizio dell'intervallo, m0 = massa perduta per il consumo di propellente, theta = angolo, formato dalla direzione del volo con l'orizzontale, e g = accelerazione di gravità (9,81 m/sec^2). In questa complessa equazione si tiene conto praticamente di tutto, come fanno gli ingegneri professionisti quando affrontano il problema di determinare la traiettoria di un missile vero.
Poiché abbiamo variazioni notevoli e rapide di spinta, velocità e massa, l'intervallo di tempo che si usa nel calcolo del volo nella fase " di spinta " non dovrebbe essere maggiore di 0,1 sec: in questo modo il primo, passo consiste nel determinare l'accelerazione media fra 0 e 0,1 sec.
Si può calcolare, la distanza coperta dal modello durante il tempo considerato, con l'equazione:
x = Vot + 0,5 A t^2 (14)
dove: x = distanza, Vo = velocità iniziale, A =accelerazione nell'intervallo di tempo, e t = tempo. La velocità finale si ottiene da questa relazione
V1 = sqr(2Ax + Vo^2) (15)
A questo punto siamo in grado di spingere il conto da 0,1 sec a 0,2 sec e così di seguito finché dura la spinta del motore. Per la fase di volo successivo le equazioni restano esattamente le stesse con la sola differenza che nell'equazione (13) F diventa zero: questo rende l'accelerazione negativa, il che vuol dire che il volo è ormai rallentato e che il modello va perciò diminuendo di velocità. Per descrivere il volo in questa seconda fase è sufficiente usare intervalli di tempo di circa 0,5 sec.
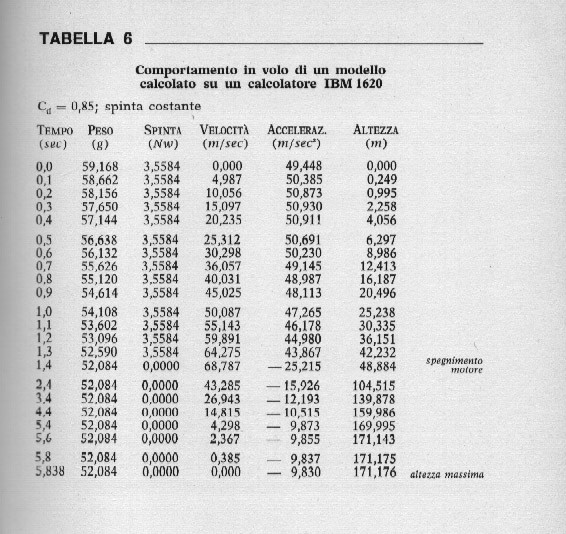
Elaborazioni di questo tipo sono lunghe e noiose ma si possono leggermente accelerare e pianificare, usando una disposizione come quella della Tab. 6, che riporta ordinatamente su righe e colonne le varie grandezze. Una volta entrati nel merito di questi calcoli si comincia ad apprezzare e a capire l'importanza di un buon progetto di una forma aerodinamica, e dell'uso di una sagoma a bassa resistenza.
C'è una considerazione interessante da fare e che forse ai principianti non potrà riuscire tanto chiara, così come a volte non lo è per i veterani. L'equazione (13) afferma che quando la spinta del motore si esaurisce e si porta a zero l'accelerazione diventa negativa. Si può cercare di ridurre la resistenza rendendo minimi i fattori Cd e s, ma è impossibile renderla nulla; durante il volo per inerzia anche m0 diventa zero, e quindi l'accelerazione è inversamente proporzionale alla massa del modello. Ne viene che, quanto più il modello è leggero, tanto più elevata è l'accelerazione, in modo tale che! le equazioni (14) e (15) forniscono valori molto più piccoli di velocità e quota. In altre parole, quanto più il modello è leggero, tanto prima è in grado di dissipare la sua quantità di moto per effetto della resistenza, cosicché raggiunge altezze relativamente modeste e in un tempo minore.
Se d'altro canto aumenta il peso, diventa minore l'accelerazione durante la fase di spinta cosicché il modello non è in grado di raggiungere alte velocità. Tra queste due esigenze esiste quindi una soluzione ottimale, che si può definire di compromesso: alleggerire troppo il modello significa danneggiarlo, perché il volo per inerzia sarà brevissimo, ma appesantirlo, troppo comporta velocità e accelerazione veramente ridicole. Calcolare matematicamente il peso, ottimale da dare al nostro modello è cosa molto difficile, per quanto non impossibile: il modellista deve affidarsi al proprio intuito e alla propria esperienza.
Mediante le equazioni (13), (14) e (15), l'autore ha calcolato il volo dell'ipotetico, razzo precedentemente scelto per il calcolo senza resistenza, assumendo lo stesso Cd trovato per il modello Aerobee-Hi nelle prove effettuate nel tunnel a vento; per ipotesi ha assunto un volo verticale, un angolo di attacco nullo e condizioni standard per determinare la densità dell'aria (volo al livello del mare e temperatura dell'aria di 25° C).
I risultati comparati appaiono in fig. 51, in cui è possibile osservare che il motore s'è spento a un'altezza ridotta (40 m), che la corrispondente velocità è diminuita fino a 80 m/sec e che l'altezza massima è solo di 300 m (cioè il 50 % circa del valore calcolabile senza tener conto della resistenza aerodinamica).
L'autore, ha poi costruito il modello cercando di realizzarlo esattamente uguale a quello che gli è servito per fare i calcoli: lo ha fatto, volare più volte con un motore del tipo B8-6 (il cui impulso totale è di 5 Nw/sec) e ne ha determinato la traiettoria e i parametri di volo con i metodi descritti più avanti; in questa maniera si è procurato un gruppo abbastanza significativo di dati sperimentali. Dalle sue misure risulta che il motore si spegne a 31 m e che l'altezza raggiunta è di circa 250 metri. I risultati sperimentali si scostano quindi leggermente da quanto calcolato, ma il fatto è spiegabile se si tiene conto cheil volo non è stato assolutamente verticale (in effetti il modello ha volato quasi sempre con un angolo d'attacco diverso da zero ed è andato soggetto a oscillazioni e deboli sbandamenti), che la forma data all'ogiva non corrispondeva perfettamente a quella provata nel tunnel a vento, e che probabilmente anche la sua levigatezza era diversa. Possono aver giocato altri fattori, che, comunque, non ci interessano.
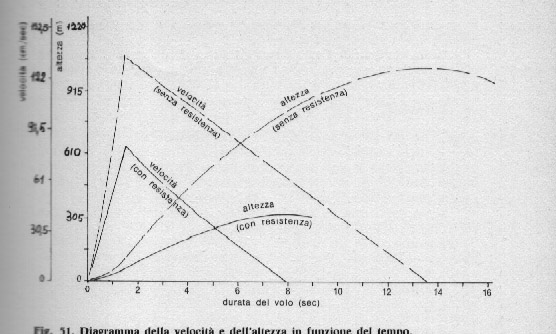
Fig. 51. diagramma della velocità e dell'altezza in funzione del tempo.
Queste prove, il calcolo precedente e l'analisi eseguita sulle equazioni ci permettono di tirare le seguenti conclusioni per puntualizzare gli effetti della resistenza aerodinamica sul volo di un modello:
1. La resistenza che anche un razzo ben aerodinamico incontra può abbassare del 40-60 % l'altezza alla quale si spegne il motore rispetto al caso di volo in assenza di aria.
2. La resistenza diminuisce l'altitudine raggiungibile - in condizioni ideali - dal razzo nel momento in cui si esaurisce la spinta del motore: questa azione diventa ancor più rilevante se la durata del motore cresce.
3. La resistenza diminuisce l'altezza massima raggiungibile in condizioni ideali di circa il 50 %, fino ad arrivare al 90 % nei casi estremi.
4. A velocità maggiori di 50 m/sec la resistenza diventa tanto elevata da richiedere sagome perfettamente aerodinamiche.
5. La resistenza assume il suo valore massimo all'istante in cui il motore si spegne; dopo di che diminuisce rapidamente fino a rendersi uguale a zero al vertice della traiettoria; un secondo dopo lo spegnimento del motore, la resistenza è già arrivata all'80-60 % del suo valore massimo.
Molti modellisti calcolano l'altezza raggiunta dai loro razzi misurando con un cronometro il tempo intercorso fra la partenza e l'arrivo al vertice della traiettoria e facendo uso dell'equazione:
s = 0,5 gt^2
dove s = altezza massima, g = accelerazione di gravità e t = tempo. Tale espressione è chiaramente approssimata perché non vi intervengono la spinta del motore, né l'espressione della resistenza aerodinamica: dà perciò risultati sempre errati generalmente per eccesso (l'errore si aggira spesso sul 300-500 %).
Per questo motivo è importante conoscere i metodi che permettono di determinare i parametri di volo, e quali strumenti si debbano usare. In un prossimo capitolo daremo sufficienti informazioni al riguardo; per ora ci accontentiamo di far presente che anche una misura fatta a occhio da una persona esperta quasi mai è attendibile, poiché in genere un modello sembra arrivare ad altezze maggiori. Ci sono modellisti che giurano di aver raggiunto la quota di 450-600 m, ma quando poi si servono di strumenti hanno la brutta sorpresa di scoprire che tutto ciò non è vero; l'errore commesso è in genere notevole, tanto che una quota di 150 m viene in genere stimata anche il doppio o il triplo. E' interessante notare che un razzo di dimensioni normali (20 mm di diametro e 25 cm di lunghezza) scompare alla vista a un'altezza di circa 350 m, cosicché a quote maggiori è possibile seguirlo soltanto osservando la scia dei gas di scarico.
Tutte le volte che l'autore si è trovato a leggere qualche resoconto di prove in cui era scritto che il modello era arrivato a 600-1200 m di altezza, ha sempre ritenuto che ci fosse di mezzo un po' di esagerazione; guardando poi le foto e i disegni ha sempre avuto conferma che la sua impressione era esatta perché dalla sagoma, dal tipo e dalle caratteristiche, risultava evidente che simili prodezze erano impossibili.
Occorre quindi fare molta attenzione, ma bisogna anche credere ai risultati ottenuti con tutte le regole cioè in presenza di giudici e con l'uso degli strumenti, anche se a volte possono sembrare quasi incredibili. Bisogna sempre ricordare che in questo hobby intervengono tanti fattori, a volte sconosciuti e assolutamente imprevedibili, che danno peraltro a questa materia un certo fascino; è bene poi ricordare che siamo nel campo della fisica, sempre suscettibile di ulteriori studi e approfondimenti.