Abbiamo già discusso i metodi generalmente usati, per calcolare l'altezza massima raggiunta da un modello in volo, e abbiamo avuto modo di renderci conto dell'impossibilità di stabilirla accuratamente a priori: alcuni dei parametri necessari al calcolo sono difatti dotati di una tale incertezza da rendere tutta la procedura molto approssimativa, e da costringerci a ricorrere a misurazioni piú precise per determinare il reale comportamento del nostro modello.

E' soprattutto il coefficiente adimensionale di resistenza aerodinamica che non può essere determinato con sufficiente precisione, ed è dotato di un tale margine di errore da rendere tutti i calcoli puramente indicativi. Solo con metodi matematici raffinati, e mediante l'uso di un calcolatore elettronico, è possibile effettuare difatti un calcolo abbastanza preciso: queste procedure sono però appannaggio degli scienziati che lavorano nei centri missilistici veri e propri, perché le cognizioni matematiche e le spese che comportano sono tali e tante, da non poter essere sopportate da un normale modellista.

Del resto anche a Cape Kennedy o a White Sands si è presentato il problema di determinare l'altezza raggiunta da un missile per via sperimentale: sono stati così introdotti dispositivi elettronici come il radar, od ottici come i telescopi: con questi strumenti gli scienziati sono in grado di seguire il missile e avere a disposizione quei dati che, convenientemente elaborati, consentono di eseguire una misura ragionevolmente accurata delle prestazioni di volo e della posizione del missile nello spazio.

Anche nel razzimodellismo si usa fare qualcosa del genere, naturalmente con mezzi molto più semplici e soprattutto molto meno costosi: gli strumenti elettronici sono pertanto generalmente da escludere a causa del loro alto costo, della loro complessità, e della conoscenza di tecniche elettroniche che richiedono. Inoltre, un modello di missile non si presta bene ad essere seguito da un radar a causa della piccola superficie e perché costruito generalmente con materiale non metallico. Per questa ragione, e anche per amore di semplicità, i modellisti si servono di strumenti ottici, quali i telescopi o i teodoliti.

Chi ha pratica di gare di missili o si è trovato in qualche poligono di tiro, si sarà senz'altro reso conto del fatto che determinare l'altezza massima raggiunta da un missile non riveste nessuna difficoltà, anche se a volte è necessario l'intervento contemporaneo di due o più persone: questo tipo di misurazione è ormai abbastanza diffuso, ed è usato anche da gente dotata di poche cognizioni specifiche. Tutto quello che si richiede è una normale conoscenza di matematica, e soprattutto di trigonometria, che è indispensabile per la elaborazione dei dati e per effettuare quei pochi calcoli che permettono di risalire dalle grandezze effettivamente misurate, alle grandezze che invece ci interessano; nelle pagine successive ci soffermeremo brevemente a descrivere questo punto e a spiegarne tutta la procedura di calcolo.

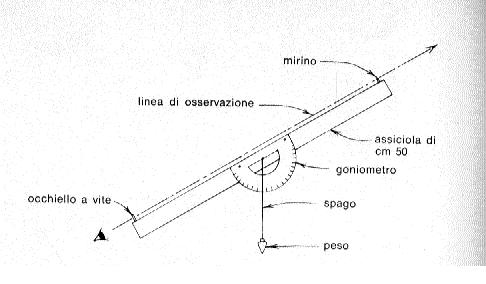
Esistono due metodi di controllo ottico, uno atto a fornire un valore approssimato, e uno molto accurato, usato per le gare.

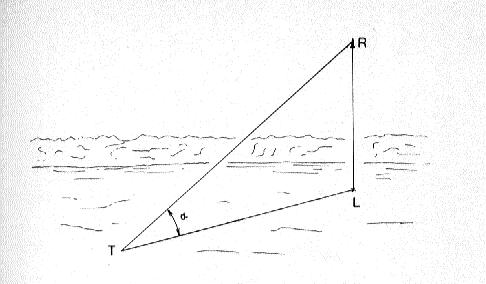
Il primo sistema, che è decisamente quello più semplice, si serve di un dispositivo di osservazione che misura l'angolo di elevazione del modello rispetto a una stazione di controllo posta a una distanza nota dal punto di lancio, e richiede due persone: una che provveda al lancio del modello e una che lo segua visivamente. Un tale sistema può essere molto semplicemente costruito in casa e consiste, come si può vedere in fig. 135, in uno strumento per l'osservazione di razzi in volo, formato essenzialmente di un dispositivo per la determinazione dell'angolo di elevazione: a questo scopo può bastare un normale goniometro scolastico e un filo a piombo. La fig. 136 mostra il principio geometrico su cui si fonda il metodo: L è il punto di lancio, T è la stazione di controllo (la cui distanza da L è nota), R è il punto di massima altezza della traiettoria, supposta perfettamente verticale descritta dal modello, e alfa è l'angolo di elevazione che l'osservatore legge direttamente sul suo strumento. Come si vede dalla figura, congiungendo ì tre punti L, T, R, si ottiene un triangolo rettangolo; in base poi a un importante teorema di trigonometria, la tangente dell'angolo di elevazione alfa è uguale al rapporto fra l'altezza massima raggiunta dal modello (segmento L-R) e la distanza fra il punto di lancio e la stazione di controllo (segmento T-L); in simboli si può scrivere:

Tg alfa = LR/TL (1)

da tale relazione possiamo ricavare la grandezza R:

LR = TL x tg alfa (2)

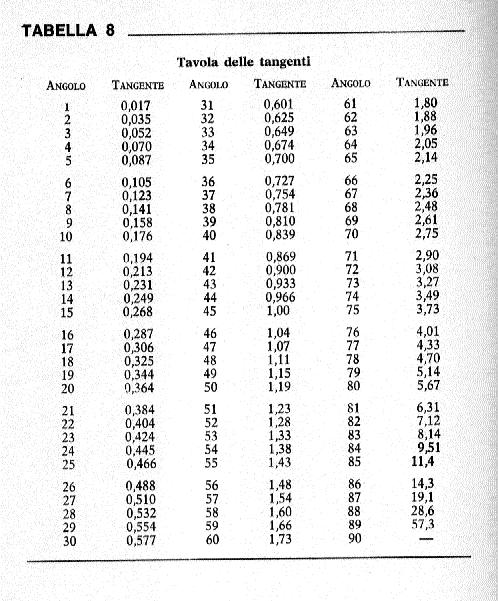
Conoscendo cosi la distanza fra il punto di lancio e l'osservatore, TL, e ricavando dalla tabella 8 la tangente dell'angolo di elevazione alfa misurato, è semplice calcolare l'altezza raggiunta dal modello nel suo volo. Un esempio pratico può essere utile nella comprensione di questo metodo: supponiamo che la stazione dì controllo si trovi a 150 m dal punto di lancio e che, per questo particolare tipo di volo, l'angolo di elevazione del modello sia di 32°; dalla tabella possiamo leggere che la tangente corrispondente a questo angolo è 0,625. La soluzione è allora molto semplice: basta moltiplicare il valore della tangente per la distanza fra l'osservatore e il punto di lancio (150 m); il nostro modello avrà raggiunto perciò un'altezza di

150 x 0,625 = 94 m.

Questo metodo sembra abbastanza preciso e in grado di fornire valori esatti: in realtà esso presenta gravi limitazioni perché alla sua base c'è l'ipotesi che il volo del modello segua una traiettoria perfettamente verticale. Chiunque abbia effettuato almeno un volo, sa difatti che il modello segue in genere una traiettoria curvilinea e che quindi l'ipotesi di cui si parlava è generalmente inattendibile. Questo fatto è sufficiente per introdurre nel metodo di calcolo una tale imprecisione da renderlo inadatto non appena si vogliano avere dei risultati sufficientemente precisi. Chi ha una minima conoscenza di trigonometria, può rendersi conto che l'errore è particolarmente sensibile, soprattutto nel caso che il vento spiri in direzione dell'osservatore e tenda quindi a far avvicinare il razzo alla stazione di controllo: è noto difatti che le variazioni della tangente sono molto più spiccate in corrispondenza dei grandi angoli piuttosto che di quelli piccoli. In conclusione, questo sistema dì osservazione può essere usato per un rilevamento grossolano dell'altezza raggiunta dal modello solo nel caso in cui si usi l'accortezza di fissare la sezione di controllo in un punto dove il vento spira nella direzione della rampa di lancio: in questo caso infatti il modello si allontana dall'osservatore, che commetterà perciò un errore minore perché le variazioni della tangente collegate a una rilevazione dell'angolo in difetto sono meno sensibili che nel caso contrario.

Per poter fornire dati attendibili sull'altezza raggiunta da un modello, un buon strumento di rilevazione deve perciò essere in grado di determinare non solo l'angolo di elevazione, ma anche l'angolo azimutale, cioè quello formato dalla linea di base con la retta congiungente la stazione di osservazione e la proiezione sul terreno del punto di massima altezza (fig. 141). Di questo strumento, chiamato teodolite sono stati costruiti e posti in commercio da tempo i più svariati tipi, che vanno da quelli molto semplici e poco costosi a quelli di precisione, che si avvalgono dell'ausilio di telescopi a basso potere risolutivo e a largo campo.

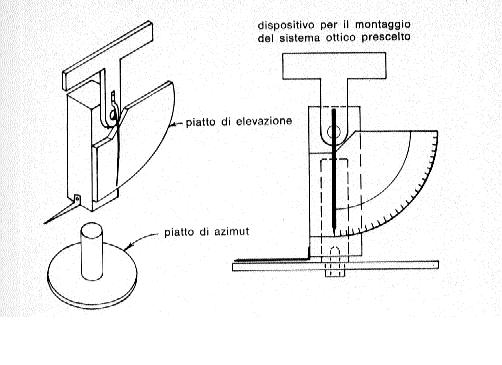
Nella fig. 138 è riportato lo schema generale di montaggio di un teodolite altazimutale, che può però assumere le più svariate forme e dimensioni e può essere costruito con i più disparati materiali: per la sua sistemazione sul campo di gara è sufficiente montarlo su un semplice cavalletto per macchine fotografiche. Se uno non vuole o non ha la possibilità di acquistare uno dei tanti tipi di teodolite disponibili in commercio, può sempre costruirsene uno in casa, utilizzando normali goniometri scolastici in vendita nelle cartolerie: in questa maniera si realizza uno strumento non certo di precisione, ma che è però in grado di fornire una misura ancora sufficientemente precisa e comunque migliore di quanto si riuscirebbe a fare con il primo sistema.

Se i modelli non raggiungono altezze elevate e possono essere quindi seguiti a occhio nudo, il sistema di puntamento può consistere in una semplice asticciola diritta di legno o di metallo con infissi, a una estremità un occhiello a vite che funge da oculare, all'altra un chiodo che funge da mirino: in questa maniera, guardando attraverso l'occhiello la punta del chiodo, si riesce a seguire il missile utilizzando lo strumento come se fosse una specie di piccolo fucile. Volendo invece realizzare qualcosa di più raffinato, si può utilizzare un tubetto metallico del diametro di 2 o 3 cm e lungo circa 30 cm, con uno spioncino all'estremità rivolta verso l'osservatore, attraversato da un filo sottile che funge da traguardo: anche in questo caso è necessario però che il modello sia seguibile a occhio nudo per tutta la sua traiettoria. Quando ciò diventa impossibile a causa dell'elevata altezza che il modello raggiunge, è necessario infatti ricorrere a un ausilio ottico, cioè a un telescopio. Generalmente il principiante è portato in questo campo a servirsi di un telescopio a forte ingrandimento, perché pensa che così facendo migliora la visibilità e la possibilità di seguire il suo modello: in realtà è sconsigliabile seguire questa direttiva perché, quanto maggiore è la potenza dì questo strumento, tanto più è ristretto il campo visivo che esso offre e, quindi, più difficile seguire il modello. In linea di massima si può dire che un mirino da telescopio da carabina con ingrandimento 1 o 2 fornisce una eccellente soluzione per il nostro problema, anche tenendo conto del basso costo: il campo visivo offerto è difatti sufficiente per seguire abbastanza facilmente il modello in volo.

In questo campo non mancano naturalmente esempi di teodoliti abbastanza complicati e relativamente costosi, costruiti utilizzando telescopi a gomito a 10 ingrandimenti e caratterizzati da un campo visivo di 10°: naturalmente la scelta dipende dalle esigenze che ha il modellista e da quanto è disposto a spendere. C'è anche da dire che questi teodoliti non sono spesso proprietà di un singolo aeromodellista, ma sono piuttosto in dotazione del poligono di tiro e quindi comperati collegialmente da tutti i partecipanti. In questo modo è possibile indirizzarsi verso le soluzioni più costose, e giungere a soluzioni abbastanza raffinate e peraltro molto comode: in qualche poligono di tiro americano, l'autore ha avuto modo di vedere teodoliti che si servono di utilissimi filtri di vari colori, in maniera da permettere di seguire il modello in volo nelle più disparate condizioni di luce: ad esempio, se si dipinge il modello con una vernice fluorescente arancione e si usa un filtro rosso, il modello appare bianco sullo sfondo di un cielo nero. Non è il caso di far notare che in questa maniera diventa molto facile seguire il modello in volo, ma, piuttosto, che l'uso di questi strumenti diventa abbastanza difficoltoso e riservato a persone esperte. In quanto alla precisione, possiamo però dire che non esiste una grande differenza fra i tipi meno costosi e quelli più raffinati, purché il modello resti visibile a occhio nudo.

Per l'osservazione di modelli in volo sono necessari due teodoliti: questi vanno sistemati in una posizione tale che ognuno possa chiaramente vedere l'altro e contemporaneamente la rampa di lancio. Per le misure normali, la distanza fra un teodolite e l'altro deve aggirarsi attorno ai 150 m circa, mentre per le competizioni nazionali, dov'è indispensabile la massima precisione, tale distanza può salire anche a 600 m; la posizione rispetto alla base di lancio non ha particolare importanza, purché, come si è detto, i due teodoliti siano chiaramente visibili fra loro.

Esistono però alcuni accorgimenti da rispettare nella sistemazione dei due teodoliti: infatti, perché la misura possa essere effettuata accuratamente, è necessario che gli angoli azimutali alfa e gamma (fig. 141) abbiamo un valore di almeno 10°; inoltre, data la velocità del missile, le due stazioni di osservazione devono essere collocate a non meno di 90 m dall'area di lancio, perché sia possibile seguire la traiettoria del modello. Come ultimo accorgimento, abbastanza importante, è necessario che i due teodoliti siano disposti a sud-ovest e a sud-est della rampa di lancio, per evitare che l'uno o l'altro dei due operatori sia costretto a osservare il modello contro sole. La fig. 141 mostra lo schema di sistemazione: i teodoliti devono essere collocati nei punti scelti e disposti a livello finché gli angoli azimutali non siano perfettamente orizzontali. Si eseguono prima le necessarie operazioni di taratura e, quando tutto è pronto per effettuare la misura, il modello può partire. I due operatori lo seguono con i teodoliti, e quando la massima altezza viene raggiunta, fissano i loro strumenti nella loro posizione finale e leggono nei rispettivi quadranti il valore dell'angolo azimutale e di quello di elevazione, che successivamente portano o comunicano telefonicamente alla base di lancio.

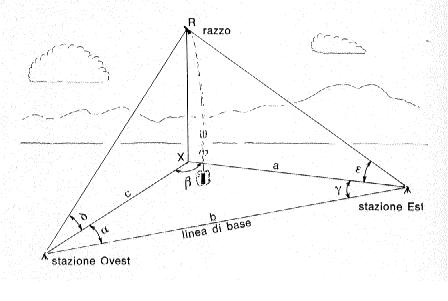
Vediamo ora, facendo sempre riferimento alla fig. 141, come si può ricavare l'equazione che ci permette di calcolare l'altezza raggiunta dal missile, e di spiegare con maggiore esattezza che cosa si intenda per angolo azimutale e per angolo di elevazione. I dati, che sono noti perché suscettibili di essere misurati, sono:

la distanza b

l'angolo alfa

l'angolo beta

l'angolo gamma

l'angolo epsilon

l'angolo delta.

Facendo riferimento alla figura sopra citata, e notando che il punto X rappresenta il piede della perpendicolare condotta al terreno dal punto di massima altezza, l'altezza da determinare è rappresentata dalla distanza RX, cioè dal cateto comune del triangolo rettangolo verticale RXO. Chi ha una minima conoscenza di trigonometria può a questo punto rendersi conto che, per determinare la posizione di X è necessario determinare le due distanze a e c. A questo scopo torna utile la legge trigonometrica per cui esiste una proporzionalità diretta fra i lati di un triangolo e il seno dell'angolo opposto, in maniera da poter scrivere:

c/sen gamma = b/sen beta=a/sen alfa

da cui si può ricavare c:

c=sen gamma (b/sen beta)

Servendosi inoltre della nota relazione fra gli angoli interni di un triangolo rettangolo, che stabilisce la loro somma sempre pari a 180° si può scrivere:

c = sen gamma x b/sen(180-(alfa+gamma))

Poiché però R è per definizione sulla verticale di X, si può notare che l'angolo RXO è un angolo retto e perciò diventa possibile calcolare il cateto RX mediante la nota relazione:

tg delta = RX/c

Sostituendo in questa formula il valore di c calcolato precedentemente, si ottiene la seguente equazione:

RX = sen gamma tg delta (b/sen(180-(alfa+gamma)))

in cui tutte le grandezze sono note perché misurate con i teodoliti. Si può ripetere lo stesso ragionamento e calcolare l'altezza RX servendosi del triangolo rettangolo RXE e trovando quindi una relazione analoga, la quale utilizza angoli azimutali e di elevazione misurati dall'altra stazione di rilevamento:

RX = sen alfa tg epsilon (b/sen(180-(alfa+gamma)))

E' intuitivo che le due procedure di calcolo debbono fornire fra loro valori simili: in linea di massima si può dire che una divergenza attorno al 10 % è senz'altro attribuibile a errori sperimentali, ma che una divergenza più forte dei due valori è da attribuire a errori grossolani di determinazione ed è quindi sintomo di scarsa attendibilità di almeno una delle due misure. In questo caso l'altezza raggiunta dal modello non può essere ritenuta misurata con sufficiente accortezza, e pertanto, se ci si trova in una gara, la prova va ripetuta. In caso contrario, quando cioè i due valori differiscono fra loro meno del 10 % si ricorre a una media delle due misure, che viene assunta come il valore più probabile di altezza raggiunta dal modello.

A questo punto si potrebbe introdurre un discorso abbastanza lungo e complicato sull'incertezza relativa a questi dati sperimentali e su come si possa fare per migliorarli o per lo meno per conoscerne l'ordine di approssimazione. In linea di massima basta dire che gli angoli vengono ricavati con l'approssimazione di 1°, il che comporta una certa incertezza sul valore di X ricavato dalle formule. Si adotta pertanto un sistema di compensazione, inteso come una correzione o un arrotondamento in grado di alleggerire il valore ottenuto dalle cifre decimali ritenute insignificanti. Il mezzo più usato è quello di arrotondare a 10 il valore medio ottenuto: se cioè la cifra dell'unità è compresa fra 1 e 4, essa viene portata a 0, se compresa fra 6 e 9 viene ancora portata a 0, aumentando però di 1 quella delle decine; il 5, infine, viene soppresso se la cifra delle "dozzine" è pari, mentre se dispari, viene portato a 0 aumentando di 1 la cifra delle dozzine; esempio: 141 diventa 140, 147 diventa 150, 145 diventa 140 e 155 diventa 160. Questa regola può sembrare abbastanza empirica al principiante e priva di qualsiasi sostegno teorico: in realtà solo una persona pratica di calcolo numerico e che riesca a rendersi conto del significato effettivo del numero che trae dalla sua esperienza, può senz'altro capire perché si opera in questa maniera.

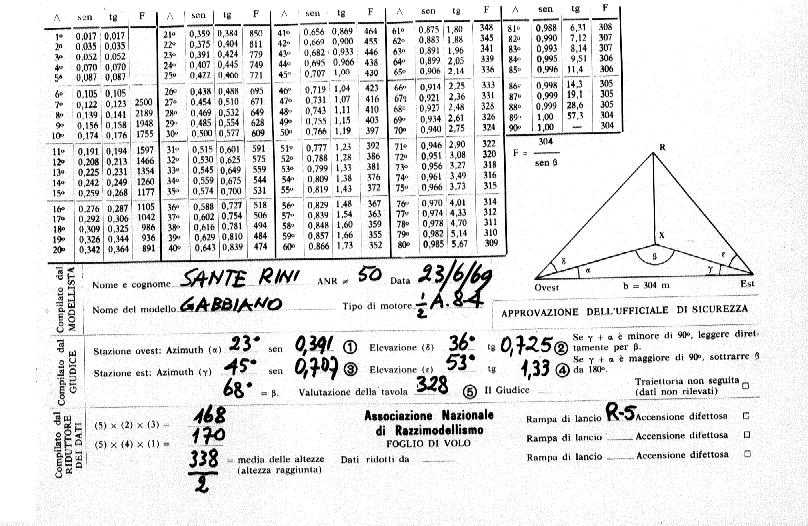
Vediamo ora un esempio pratico della elaborazione dei dati di un esperimento. Siano essi:

linea di base 304 m

angolo azimutale rilevato dalla stazione est (gamma = 23°)

angolo di elevazione rilevato dalla stazione est (epsilon = 36°)

angolo azimutale rilevato dalla stazione ovest (alfa = 45°)

angolo di elevazione rilevato dalla stazione ovest (delta = 53°)

Per il primo triangolo l'equazione è:

RX = sen gamma tg delta(b/sen(180°-(alfa+gamma)))=

=sen 23° tg 53° (304/sen(180°-(45°+23°)))=

=0,391 x 1,33 x (304/sen 68°)=

=0,391 x 1,22 x (304/0,927)=

=0,391 x 1,33 x 328=

=171 metri

La soluzione dell'analogo calcolo sull'altro triangolo dà un valore di 169 m, in ottimo accordo con quanto calcolato precedentemente: possiamo ora calcolare la media e ottenere cosi un valore pari a 170 m. Facendo questi calcoli, ci si rende conto che il termine di destra dell'equazione sotto forma di frazione è il termine più complesso e riappare risolvendo l'altro triangolo, per cui risulta vantaggioso tabularlo (vedi fig. 143, fattore F).

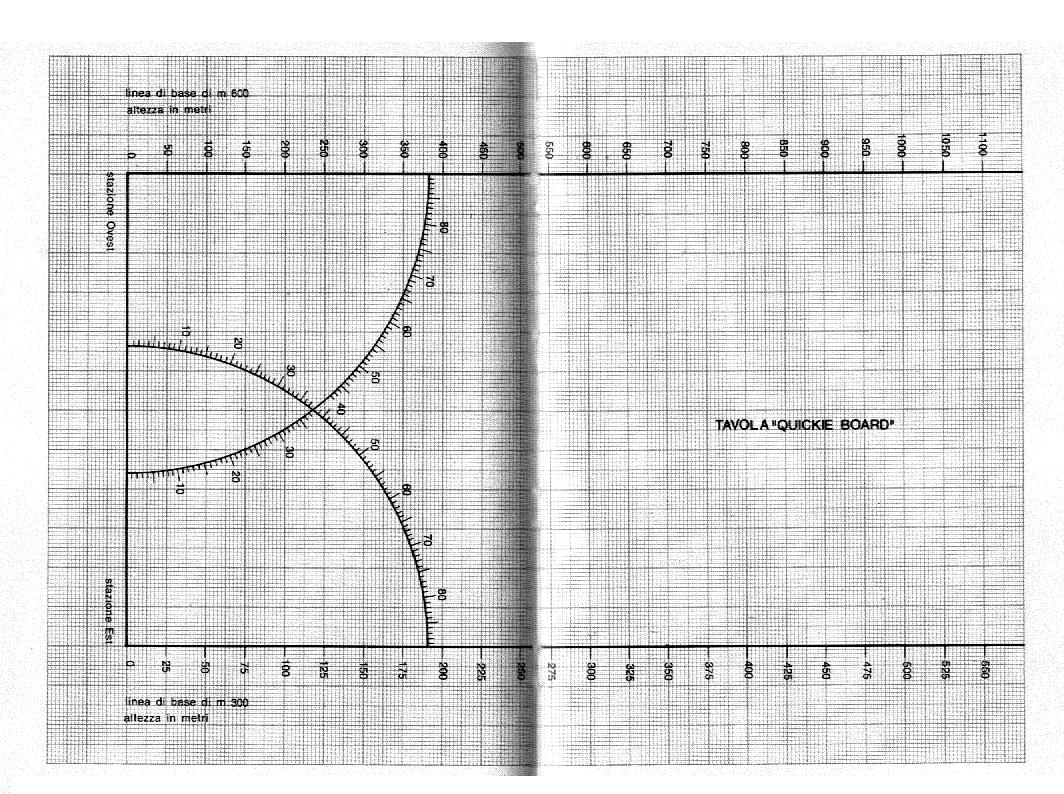
Anche in questo campo non mancano però soluzioni ingegnose per calcolare direttamente senza troppa difficoltà l'altezza massima raggiunta da un modello, ingegnosi diagrammi, del resto abbastanza semplici e tali da facilitare il calcolo. John Roe di Colorado Springs (Colorado) ha elaborato un metodo che merita di essere citato perché fornisce il modo di registrare i dati in una maniera abbastanza razionale e intelligente, così che basta poi effettuare alcune semplici operazioni algebriche per ottenere il risultato. In fig. 143 viene riportato il foglio di volo che, dietro consiglio di John Roe, viene consegnato a ogni modellista al momento della gara, e su cui sono stampate per comodità le tavole per il calcolo dei seni, delle tangenti, e del fattore F. In questo modo si ha bisogno, al poligono di tiro, solo di un normale regolo, che può essere tenuto comodamente in tasca e non dà nessun disturbo. Di tutt'altra natura è invece il metodo elaborato da John e Jim Bonine, di Denver (Colorado), che hanno messo a punto nel 1960 un metodo di calcolo, denominato " Quickie Board " riportato in fig. 140 in forma modificata. Questo metodo, nonostante sia di natura grafica, è tuttavia molto accurato, e va pertanto consigliato anche perché è molto pratico e in grado di fornire valori sufficientemente precisi. Come si può vedere dalla figura, sono state disegnate due rette verticali, graduate per linee di base di 300 e 600 m, e due cerchi simmetrici, con centro nei due punti angolari del diagramma, e suddivisi in 90 parti, ognuna delle quali corrisponde a un grado. Per calcolare l'altezza raggiunta da un modello bisogna seguire questo procedimento:

1. Il vertice di destra corrisponde per esempio alla postazione di rilevamento est e quello di sinistra alla postazione di rilevamento ovest.

2. Riportato sui rispettivi archi il valore degli angoli azimutali rilevati dagli osservatori, si tracciano due rette, passanti per le origini e i punti rilevati e intersecantesi fra loro.

3. Per calcolare il triangolo ovest fare centro sull'origine corrispondente con un compasso e riportare sull'ascissa il punto d'incontro delle due rette disegnate precedentemente.

4. Dal punto così determinato sull'ascissa innalzare una retta perpendicolare.

5. Sul rispettivo arco graduato, riportare il valore dell'angolo di elevazione rilevato da ovest e tracciare una nuova retta che passa per l'origine ovest e il punto ora trovato.

6. Il punto di incontro fra questa retta e la verticale ottenuta in elaborazione 4 rappresenta l'altezza raggiunta dal modello, che verrà letta sull'una o sull'altra delle ordinate a seconda che la linea di base sia di 300 o 600 m. Per il calcolo del triangolo est il procedimento è perfettamente analogo.

In fig. 146 è riprodotto invece un altro sistema di elaborazione rapida e sicura messo a punto da Vernon Estes, chiamato " 3-D Board " o " Tavola tridimensionale ". Esso consiste in un pannello in scala, su cui viene riprodotta la dislocazione della base di lancio e delle stazioni di osservazione, rappresentate da due indicatori degli angoli azimutali e di elevazione - posti a una distanza l'uno dall'altro proporzionale a 300 m - da cui si dipartono due fili di acciaio che riproducono le linee di osservazione. Dopo aver regolato i due indicatori sui valori rilevati durante l'esperimento, si tirano i due fili di acciaio: l'altezza massima raggiunta dal missile è rappresentata dalla distanza fra la loro intersezione e il pannello, e viene misurata con un regolo in scala, su cui si può leggere direttamente il valore in metri.

In alcuni poligoni di tiro, è poi possibile vedere strumenti di rilevamento e di calcolo veramente elaborati; da qualche parte si è giunti addirittura all'uso di semplici calcolatori analogici, che possono essere costruiti con una spesa ragionevole, e che si dimostrano piuttosto utili perché di facile applicazione e capaci di fornire risultati abbastanza precisi. Con tali calcolatori si può pensare addirittura di automatizzare completamente tutte le operazioni di calcolo dell'altezza raggiunta da un modello, collegando semplicemente all'indice di misurazione dell'angolo di azimut e di elevazione dei due telescopi due autosincronizzatori o potenziometri i cui impulsi elettrici costituiscono i dati di partenza del calcolatore analogico, che poi provvede automaticamente a elaborarli per fornire i risultati.

Nei primi poligoni di lancio si usava quasi sempre registrare sul foglio i dati di volo e portarli soltanto in un tempo successivo alla base: solo a questo punto venivano elaborati, ma si perdeva tempo prezioso e la possibilità di scambiarsi reciprocamente informazioni utili. Per motivi di questo genere si preferisce stabilire un collegamento diretto continuo fra gli addetti alle azioni effettive di lancio e i due operatori che lavorano ai teodoliti. In questa maniera è possibile tenersi costantemente informati su quanto sta succedendo, fornire indicazioni su colori, numeri di stadi e prestazioni previste del modello che si sta per lanciare e dare eventualmente l'allarme nel caso che qualche cosa non stia andando per il giusto verso. Non è poi da sottovalutare la possibilità di fornire indicazioni sull'aspetto esteriore del modello, perché in questa maniera diventa molto più facile individuarlo in volo e seguirne la traiettoria.

Fra i tanti sistemi che sono stati sperimentati, vanno citati le segnalazioni con bandierine, i radiotelefoni, gli altoparlanti, i telefoni da campo ecc.; è chiaro che il più economico, e che quindi sembra prestarsi meglio ai nostri scopi, è rappresentato da un sistema di segnalazioni a bandierine, che però presenta il grave inconveniente di essere scarsamente funzionale e soggetto a un numero rilevante di errori. Soprattutto se si è in grado di suddividere la spesa fra varie persone, si preferisce generalmente ricorrere a un'installazione di telefoni da campo, proprio per la possibilità che si ha di comunicare. Anche il radiotelefono offre un vantaggio di questo tipo, ma unisce l'inconveniente di non essere un sistema a due vie, mentre con il telefono da campo è possibile effettuare una vera e propria conversazione e scambiarsi quindi idee, opinioni e tutti quei dati che si ritiene utile per il buon esito della gara.

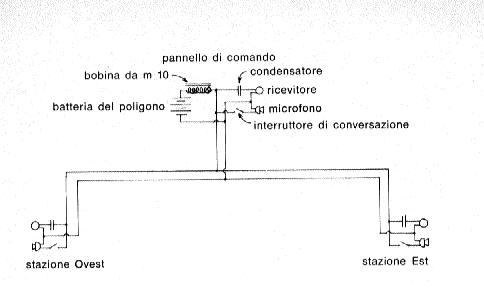
Realizzare un impianto di telefono da campo non è difficile: innanzitutto è necessario disporre di una linea a due cavi, in modo che il circuito sia chiuso, perché il sistema di un cavo solo è spesso di difficile realizzazione, in quanto utilizza come cavo di ritorno il terreno la cui conducibilità è molto variabile. Il cavo necessario è facilmente in commercio, e negli Stati Uniti può essere acquistato anche presso i magazzini dell'esercito e della marina che vendono il materiale superfluo: in linea di, massima esso è composto da fili intrecciati e isolati da un rivestimento di plastica. Nei poligoni permanenti, e che praticamente funzionano tutto l'anno, il sistema di fili può essere interrato, mentre quando il poligono ha un carattere di provvisorietà o ne è previsto il funzionamento solo per breve tempo, esso può essere facilmente installato in poche ore e recuperato alla fine della giornata di esperimenti; a Hogback, la linea sotterranea realizzata nel 1959 funziona ancora perfettamente. Per quanto riguarda la sorgente dell'energia elettrica, non esistono difficoltà: è sufficiente consultare il catalogo di qualche ditta specializzata in elettrotecnica per trovare una batteria che faccia al caso. Esistono normalmente tre comuni sistemi telefonici: il più semplice e meno costoso è quello realizzato da Wheeler, reperibile ora in commercio in versioni diverse, e caratterizzato dal fatto di non. avere bisogno di energia elettrica poiché funziona con i soli impulsi generati dai telefoni. Questo tipo di telefono da campo assicura una ricezione sufficientemente chiara anche se di basso volume e richiede, oltre alla linea, tre speciali cornette, che vengono sistemate nei punti corrispondenti alla base di lancio e alle due stazioni di osservazione, secondo lo schema riportato in fig. 147.

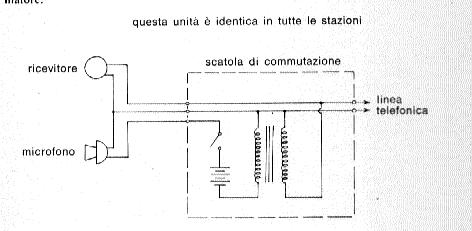
Gli altri sistemi, normalmente indicati come " sistema a corrente continua " (Sistema CC) e " sistema con trasformatore ", richiedono invece anche altre parti ausiliari e soprattutto una sorgente di elettricità. In linea di massima si presentano quindi più costosi e di più difficile realizzazione, ma sono anche caratterizzati da una migliore ricezione; oltre alle normali cornette telefoniche si possono anche usare poi cuffie di ricezione con un minuscolo microfono laterale, del tutto simili a quelle in dotazione alle centraliniste. I ricevitori di cui si valgono questi due dispositivi consistono in un magnete e una bobina, e non hanno bisogno di alcuna corrente poiché sono messi in funzione dai soli impulsi elettrici corrispondenti ai segnali sonori inviati dai microfoni. I due sistemi differiscono solo nel metodo usato per fornire il voltaggio (da 1,5 a 6 V) necessario al funzionamento dei microfoni, i quali appartengono quasi sempre al tipo cosiddetto a carbone. La fig. 148 rappresenta lo schema di voltaggio del sistema CC; come sorgente centrale si può usare la stessa batteria che provvede all'accensione dei razzi, alla quale bisogna solo collegare in serie una piccola bobina per evitare che le audiofrequenze la mettano in corto circuito. L'inserimento della batteria assicura in tutta la linea il passaggio di una corrente continua che serve da corrente di fondo per facilitare la trasmissione degli impulsi elettrici generati dal microfono, che deve essere dotato di un interruttore, in quanto trasmette anche una quantità di suoni di fondo a causa della grande potenza di questo sistema telefonico; l'interruttore ha lo scopo di disinserirlo dal circuito in modo da evitare che provochi disturbi quando l'operatore non lo stia usando, ovvero quando stia ascoltando al ricevitore. Consideriamo ora il ricevitore: abbiamo già visto che esso raccoglie impulsi elettrici provenienti dal microfono ritrasformandoli in suoni. E' necessario perciò escluderlo dalla corrente di linea che lo renderebbe completamente inefficiente: per fare ciò è sufficiente applicare, immediatamente prima del ricevitore, un semplice e poco costoso condensatore di capacità adeguata, il cui solo scopo è di far passare le audiofrequenze bloccando invece la corrente di linea.

Il sistema con trasformatore, il cui schema è riportato in fig. 149, consiste invece in: una cuffia con microfono, un interruttore per l'esclusione di quest'ultimo, una batteria per circuito microfonico (che può essere anche una semplice batteria per torce elettriche), e un trasformatore di isolamento che ha la funzione di escludere il microfono e bloccare la corrente di linea al ricevitore; tutta questa apparecchiatura viene poi racchiusa in una cassetta. Il sistema presenta il vantaggio di poter essere inserito anche in rete telefonica pubblica, e perciò, anche se sensibilmente più caro degli altri, è stato adottato in molti poligoni.