saccheri

Il postulato quinto sfugge ad ogni verifica sperimentale e non ha il carattere di "evidenza" degli altri quattro, e di questo si era reso conto lo stesso Euclide che sembra voler differirne il suo uso il più possibile.

Egli, infatti, come abbiamo visto, era riuscito a dimostrare 28 proposizioni basandosi solo sui primi quattro postulati, e aveva dimostrato l'esistenza di rette parallele con la proposizione 28: Se due rette intersecate da una trasversale soddisfano certe relazioni angolari (ad es. formano angoli alterni interni uguali), queste rette se prolungate infinitamente non si incontrano; e con la proposizione 31: Per un punto dato, non giacente sulla retta né sul suo prolungamento, è possibile tracciare una retta parallela alla retta data.

Si trattava poi di dimostrare l'inverso di tale teorema per completare e rendere rigorosa la teoria del parallelismo, dimostrare cioè che, se due rette sono parallele, esse, tagliate da una trasversale, soddisfano quelle relazioni angolari (proposizione 29).

Questa proposizione è inoltre indispensabile per i successivi sviluppi della teoria assiomatico-deduttiva: su di esso ad esempio si fonda il teorema 32: in ogni triangolo la somma dei tre angoli interni è pari a due retti.

Non solo, E. aveva dimostrato, basandosi solo sui primi quattro postulati, il teorema 17: la somma di due angoli interni di un triangolo è minore di due retti che è, come abbiamo visto, la proposizione inversa del quinto postulato.

«Può mai essere un postulato l'inversione di un teorema già dimostrato?», si chiedeva Proclo (secolo V d.C.) esponendo le perplessità che erano già state prospettate da precedenti commentatori di Euclide.

Per quasi duemila anni, dal III secolo d.C. alla metà dell'Ottocento, schiere di pensatori si posero il problema del quinto postulato nel quale vedevano una deficienza del perfetto meccanismo della geometria euclidea, e così intrapresero tentativi di dimostrarlo a partire dagli altri, ma, il più delle volte, l'effetto che si sortiva era quello di sostituirlo, tacitamente o esplicitamente con proposizioni ad esso equivalenti.

a) In un piano il luogo dei punti equidistanti da una retta è ancora una retta.

b) In un piano la somma degli angoli interni di un triangolo è uguale a due retti.

c) Di ogni figura piana ne esiste una simile di grandezza arbitraria (due poligoni si dicono simili quando i loro angoli sono congruenti e i lati corrispondenti ad angoli congruenti sono nello stesso rapporto).

d) In un piano, per un punto fuori di una retta si può condurre una e una sola retta parallela a una retta data (due rette si dicono parallele, come per Euclide, quando non si incontrano).

Quest'ultimo, noto come Postulato di Playfair (1748-1819), è quello che viene più spesso usato in sostituzione dell'originale Quinto postulato euclideo.

Dimostriamo l’equivalenza logica tra i due postulati. Dobbiamo cioè dimostrare che:

1. Supponiamo, per assurdo, che esista un’altra retta t parallela alla retta r e passante per P; (RAA);

Vengono utilizzati, nella dimostrazione del teorema, gli assiomi della geometria assoluta e il teorema 30 (nel passo2.) il quale è stato dimostrato da Euclide per mezzo del Quinto Postulato.

Ipotesi: Due rette a e b tagliate da una trasversale r formano con questa angoli coniugati la cui somma è minore di due retti;

Tesi: Le due rette si incontrano da quella parte in cui gli angoli coniugati sono minori di due retti.

2. Conduciamo da A (intersezione della retta a con la trasversale t) una retta r tale che con la retta b e con la trasversale t formi angoli coniugati la cui somma è due retti;

Il XVIII secolo è considerato il secolo dei precursori delle geometrie non-euclidee: G. Saccheri, J.H. Lambert, A.M. Legendre sono le personalità di maggior spicco.

Gerolamo Saccheri (1667-1733) Scrive nella prima pagina del suo libro: ²Euclides ab omni naevo vindicatus² (Euclide pulito da ogni macchia): «Porro nemo est, qui dubitet de veritate expositi Pronunciati; sed in eo unice Euclidem accusant, quod nomine axiomatis usus fuerit, quasi nempse ex solis terminis rite perspectis sibi ipsi faceret fidem». Nessuno dubita della verità del V Postulato (Pronunciati), si accusa soltanto E. di avere usato il nome di postulato, quasi che la convinzione nascesse dal solo enunciato correttamente inteso. Il quinto postulato è invece un teorema si tratta quindi di dedurlo dalle precedenti proposizioni.

Per giungere a questo risultato S. si avvale del ragionamento per assurdo, e in questo modo, fu il primo a prendere in esame tutte le possibili conseguenze che comporta una negazione del quinto postulato; egli infatti riteneva che, negando il postulato euclideo e ricavando tutte le proposizioni logiche che da questa negazione derivano, si sarebbe trovata una proposizione (sulla cui esistenza S. non nutriva alcun dubbio) in contraddizione con gli altri quattro postulati. Così, in realtà, S. dedusse una serie di teoremi che sono alla base della geometria non-euclidea detta iperbolica.

Scrive Heath: «Saccheri fu vittima della preconcetta convinzione del suo tempo che la sola geometria possibile fosse quella euclidea, ed egli presenta lo spettacolo curioso di un uomo che erige a fatica una struttura su nuove fondamenta con l'effettivo proposito di demolirla in seguito, cercando contraddizioni nel cuore del sistema che egli stesso aveva costruito per dimostrare la falsità della sua ipotesi».

S. prende le mosse dalla considerazione di una figura fondamentale, il quadrilatero birettangolo isoscele ABCD (oggi noto come quadrilatero di Saccheri), costruito in modo che i lati AD e BC siano uguali tra loro e entrambi perpendicolari alla base AB.

In queste ipotesi, considerando prima i triangoli ABD e ACB, e poi i triangoli BCD e ACD, dimostra facilmente che ÐD = ÐC.

Se è vero che nella geometria euclidea tutti i quadrilateri di Saccheri sono rettangoli e viceversa, la dimostrazione di questo fatto dipende dal quinto postulato che S. nega. In effetti l'esistenza stessa dei rettangoli è garantita dal teorema 46 che fa uso del quinto postulato.

Per gli angoli ÐD = ÐC si possono formulare le seguenti tre ipotesi, indicate da S. come:

Dimostrando che le prime due ipotesi conducevano a risultati assurdi, Saccheri credeva di poter dimostrare la terza ipotesi che è equivalente al quinto postulato.

Dato un triangolo ABC, se dagli estremi del lato BC vengono condotte le perpendicolari BF e CG ad una retta passante per i punti medi D e E degli altri due lati, in modo da formare un quadrilatero GFBC, allora:

b) La base FG del quadrilatero ha lunghezza doppia del segmento DE che unisce i punti medi degli altri due lati del triangolo;

La somma degli angoli ÐFBC e ÐGCB è uguale alla somma degli angoli interni del triangolo.

Ipotesi: ABC è un triangolo qualunque; D e E sono i punti medi rispettivamente dei lati AB e AC; FB e GC sono le perpendicolari alla retta DE condotte dai vertici della base BC.

à La somma degli angoli interni di un triangolo è uguale a due retti, e vale il quinto postulato euclideo.

à Per un punto fuori di una retta in un piano non si può condurre nessuna parallela alla retta data.

à Per un punto fuori di una retta in un piano passano infinite rette non intersecanti la retta data, le quali sono contenute in un angolo delimitato da due rette p e q anch'esse non intersecanti la data, e costituenti gli elementi di separazione tra le secanti e le non secanti.

S. ammette sia il postulato di Archimede (dati due segmenti disuguali, esiste sempre un multiplo del minore che supera il maggiore), sia la lunghezza infinita della retta: riesce con ciò ad eliminare l'ipotesi dell'angolo ottuso (che, nell'ipotesi della finitezza della retta, conduce alla geometria non-euclidea ellittica di Bernhard Riemann). Ma l'ipotesi dell'angolo acuto lo affatica a lungo, lo costringe ad una serie di deduzioni e di teoremi che sarebbe interminabile se la dogmatica fede nell'assoluta verità della geometria di Euclide non vincesse in lui l'acuto rigore logico.

Pertanto egli afferma: "L'ipotesi dell'angolo acuto è falsa perché ripugna alla natura della linea retta ". Ciò che sarebbe contrario alla natura della linea retta sarebbe il fatto che due rette parallele avrebbero "una perpendicolare comune in un punto all'infinito", mentre egli ha prima dimostrato che al finito una retta e la sua parallela per un punto A non possono avere perpendicolari comuni (nell'ipotesi dell'angolo acuto). "La pretesa dimostrazione di S. è dunque fondata sull'estensione all'infinito di certe proprietà, valide per figure situate a distanza finita"[1]

Nel XIX secolo, periodo di rinnovamento e di ripensamento critico della matematica, trovano soluzione altri problemi posti dai geometri greci, ad esempio, quello della quadratura del cerchio e della rettificazione della circonferenza, che si riconducono alla determinazione del numero p, rapporto tra la circonferenza e il suo diametro.

Vi è però una differenza tra questi problemi e quello del V postulato. La dimostrazione di F. Lindemann (1882) del fatto che p fosse un numero irrazionale trascendente (che cioè non è radice di nessuna equazione algebrica a coefficienti razionali e che, pertanto, non è possibile costruire la circonferenza rettificata a partire dal suo raggio), presuppone una lunghissima serie di progressi, lo sviluppo di discipline sconosciute agli antichi greci, come l'algebra e l'analisi infinitesimale.

L'opera di Lobacevskij (1793-1856) (e di Bolyai (1802-1860), che poco dopo di lui raggiunse i medesimi risultati) e di Riemann invece, si basa essenzialmente sulle conoscenze della geometria dei tempi di Euclide e alcuni teoremi della sua Geometria generale sono addirittura antecedenti alla sua fondazione, trovandosi nell'opera di G. Saccheri.

Il paragone che viene fatto da più parti è quello della rivoluzione copernicana.

Nella rivoluzione non euclidea come in quella copernicana, la novità non consiste tanto o solo nell'apporto di nuove conoscenze, quanto nel capovolgimento del punto di vista.

Per Saccheri, come abbiamo visto continua ancora a sussistere il punto di vista "tolemaico" che considera il V postulato verità immobile e assoluta.

Lobacevskij, Bolyai e Riemann, invece, giunsero alla conclusione che la geometria codificata da circa due millenni negli Elementi di Euclide non era l'unica geometria pensabile e possibile, ma solo il caso limite di una geometria più generale, verificato dall'esperienza nell'ambito macroscopico ordinario; che quindi era possibile costruire più geometrie tutte perfettamente coerenti e quindi legittimate tanto quanto quella euclidea.

La scoperta della geometria non euclidea iperbolica, che si basa sull'ipotesi dell'angolo acuto di Saccheri, si deve al matematico ungherese J. Bolyai (1802-1861) e al russo N. Lobacevskij (1792-1856) che giunsero agli stessi risultati quasi contemporaneamente.

Il L. pubblicò le sue ricerche nel 1840, mentre B. parlò per la prima volta di geometria non euclidea in un'appendice di un trattato di geometria pubblicato dal padre Wolfango nel 1832, scritto che venne elogiato da Gauss che dichiarò di aver pensato "alla possibilità di uno spazio fisico corrispondente a questa nuova geometria'

Il L. dette maggior sviluppo alla parte analitica della sua geometria, mentre il B. curò più la parte sintetica.

La geometria iperbolica si basa sui primi quattro postulati di Euclide, sulle proposizioni 1-28 e 31 dimostrate da Euclide negli Elementi e su un postulato che sostituisce il Quinto postulato essendo la negazione di una proposizione ad esso equivalente (da un punto C fuori di una retta AB si può condurre una sola retta parallela ad AB).

Le linee che escono da un punto o intersecano una data retta nel medesimo piano, oppure non si incontrano mai con essa, per quanto vengano prolungate, È necessario di conseguenza, distinguere tra tali linee, relativamente a una retta data: le secanti o convergenti, e le non secanti o non convergenti, alle quali ultime appartengono le parallele, che costituiscono il passaggio dalle une alle altre,- le divergenti. Due parallele ad una retta data dividono il piano in quattro parti: in due parti opposte sono racchiuse le rette convergenti, nelle rimanenti due le divergenti.[2]

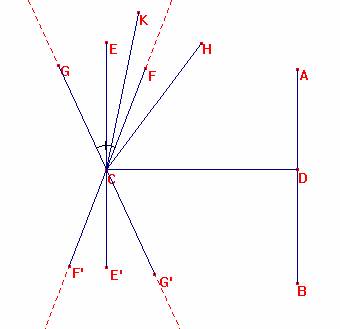
Sia AB una retta data insieme ad un punto C del piano fuori di essa. Conduciamo per C la perpendicolare CD alla retta AB, e la perpendicolare EE' alla CD.

Le rette uscenti da C devono o intersecare la retta AB come CD, o non intersecarla come la EE'. Ruotando la retta CD attorno a C in senso antiorario essa passa dalle convergenti interne all'angolo ÐFCG', alle non convergenti interne all'angolo ÐFCG, poi nuovamente, internamente all'angolo ÐGCF', passerà dai prolungamenti di quelle rette che incontrano AB; infine, alle non convergenti, interne all'angolo ÐF'CG'. Le due linee FF' e GG' che rappresentano il passaggio dalle convergenti alle non convergenti a AB, saranno parallele ad AB.

La dimostrazione rigorosa dell'esistenza della parallela CF (primo raggio uscente da C e non secante AB quando si immagini di far ruotare la retta CD attorno a C) riposa sull'applicazione del postulato della continuità di Dedekind: si dividono i raggi uscenti da C in due classi, i secanti e i non secanti; nessuna delle due classi è vuota (nella prima c'è almeno CD perpendicolare ad AB da C, nella seconda c'è almeno CE, perpendicolare a CD in C); un raggio secante precede un raggio non secante. Esiste perciò un elemento di separazione che non può appartenere alla classe dei raggi secanti, la quale non possiede un ultimo elemento; e pertanto è il primo elemento della classe dei raggi non secanti.

Lobacevskij introduce poi il verso del parallelismo. Partendo dalla posizione CD un raggio può descrivere il fascio di centro C nei due versi, antiorario e orario; al primo corrisponde il verso di percorrenza DA sulla retta AB, il secondo il verso opposto DB. Nel primo caso il primo raggio non secante è la parallela CF, nel secondo la parallela CG. Si ha così che alla retta orientata BA corrisponde la parallela orientata F'F, mentre alla retta orientata AB corrisponde la parallela orientata GG'.

[1] R.Bonola La geometria non-euclidea (Bologna, 1906).

[2] Nikolaj Lobacevskij Nuovi principi della geometria (ed. Boringhieri 1955)