1.Calcolo delle probabilità

1.1 INTRODUZIONE.

Il linguaggio del calcolo delle probabilità è pieno di esempi e applicazioni a giochi usuali quali i dadi, le carte, il lotto, ecc. e questo deriva certamente da motivazioni storiche: Pascal, Fermat, Galileo, Bernoulli, furono alcuni grandi matematici che fondarono il calcolo delle probabilità stimolati da quesiti posti dai risultati e dalle aspettative del gioco d’azzardo. Fu poi il matematico francese Laplace (1749 – 1827) a dare, nel 1812, la prima definizione di probabilità che per più di un secolo sarebbe stata dominante.

Ma esiste un’altra motivazione che deriva dal fatto che nei giochi ha senso parlare di aspettativa e fiducia in risultati che sono ripetibili e schematizzabili secondo canoni standard. Ci si augura che la realtà (biologica, economica, tecnica e sociale) possa essere schematizzata secondo modelli teorici approssimativamente riconducibili alla struttura sperimentale dei giochi sopra accennati e, soprattutto, allo schema dell’estrazione di palline da urne.

Dovendo prendere decisioni globali mediante osservazioni parziali è necessario attribuire un giudizio probabilistico a tali decisioni e quindi, a tali eventi.

La teoria della probabilità affronta il passaggio dalla popolazione ai risultati (problema diretto), l’inferenza statistica costituisce il passaggio dal campione alla popolazione ( problema inverso)

1.2 TEORIA ASSIOMATICA DELLA PROBABILITÀ

L’assiomatizzazione è un metodo tipico delle scienze deduttive e costituisce il modo moderno di affrontare le discipline scientifiche.

Si deve al matematico russo A.N.Kolmogorov (1903 – 1987) l’idea di svincolare il problema che riguarda la misura della probabilità da quello che riguarda la definizione di probabilità.

 Viene così formulata, nel 1933, la teoria assiomatica della probabilità, che consiste nei seguenti momenti:

a)      Si introducono i concetti primitivi: prova, evento, probabilità;

b)      Mediante tali concetti si stabiliscono delle proposizioni, detti postulai o assiomi, che non si dimostrano;

c)      Dai postulati, e solo tramite essi, si deducono tutte le possibili conseguenze pervenendo ai teoremi del calcolo delle probabilità.

Occorre ricordare che i postulati di una qualsiasi teoria assiomatico-deduttiva devono essere:

compatibili, cioè non contraddittori (essi cioè non possono contenere due affermazioni opposte A e non-A);

coerenti (cioè non creare contraddizioni nei risultati);

indipendenti (cioè nessuno deve contenere un’affermazione che sia conseguenza dei rimanenti).

PROVA è un esperimento soggetto a incertezza nei risultati e può essere suddiviso in sottoprove (per es. l’estrazione di più palline da un’urna).

 Ogni esperimento del mondo reale può considerarsi una prova, ma gli esperimenti di cui si occupa il calcolo delle probabilità sono quelli i cui risultati sono incerti.

Le prove della vita reale sono difficili da schematizzare, una dei modelli più usati è quella che riconduce la prova a estrazioni di palline da un’urna.

EVENTO è uno dei possibili risultati di una prova (gli inglesi dicono outcome = ciò che viene fuori.).

Gli eventi si indicano con le lettere maiuscole dell’alfabeto latino (A,B,C,…), talvolta con indici (E₁, E₂, E₃,…) e fra di essi si stabiliscono delle relazioni, proprietà e teoremi pervenendo ad un’algebra degli eventi legata alla teoria degli insiemi, anzi il matematico italiano Pompilj nella sua trattazione pone come primo postulato l’affermazione che: “Gli eventi formano un’algebra di Boole completa” il che significa che per gli eventi si stabiliscono le stesse regole e valgono gli stessi teoremi validi per una particolare classe di insiemi dell’analisi matematica (la classe di Borel).

PROBABILITÀ è un numero associato al  presentarsi di un evento e gode delle proprietà formalizzate dai postulati.

Il concetto di probabilità (e non la sua misura) si può considerare come un concetto intuitivo, originario per l’uomo: ciascuno di noi sa cosa intende quando afferma “è più probabile un ambo anziché un terno” pur non conoscendo con esattezza quel numero associato al verificarsi dell’evento ambo o terno.

Sulla teoria della probabilità sono sorte due scuole di pensiero: la scuola frequentista e quella soggettivista.

a)      Secondo i frequentisti, la definizione di probabilità si basa sulla:

 LEGGE EMPIRICA DEL CASO * (o legge dei grandi numeri ): In una serie di prove ripetute un gran numero di volte sempre nelle medesime condizioni, ciascuno degli eventi possibili si verifica con una frequenza relativa (calcolata “a posteriori”) che è approssimativamente uguale alla sua probabilità (calcolata “a priori”) e l’approssimazione è tanto migliore quanto maggiore è il numero delle prove.

DEFINIZIONE FREQUENTISTA: La probabilità è il limite della frequenza relativa di un evento ripetibile quando cresce, oltre ogni limite, il numero delle prove.

b)      Uno tra i maggiori esponenti dei soggettivisti è l’italiano De Finetti (1906-1985) che interessandosi a ricerche di tipo sociale ed economico elaborò la seguente definizione:

DEFINIZIONE SOGGETTIVISTA: La probabilità è il grado di fiducia che un individuo coerente attribuisce, in base alle proprie opinioni e alle conoscenze di cui dispone, al presentarsi di un evento, ovvero, quantificando, la probabilità è la somma p che è disposto a scommettere quando, al verificarsi dell’evento in questione, vince 1.

Il limite della definizione frequentista sta nel fatto che le prove devono essere ripetibili nelle stesse condizioni (ad es. per gli eventi “quel modello di vettura avrà successo”, il candidato X vincerà le elezioni”,…).

Il limite della definizione soggettivista sta nella difficoltà di quantificare la probabilità.

Entrambe le scuole però pervengono agli stessi postulati e dimostrano gli stessi teoremi.

1.3 ALGEBRA DEGLI EVENTI

OPERAZIONI TRA EVENTI

1.      UNIONE O SOMMA LOGICA fra due eventi A e B è quell’evento C che si verifica quando si verifica almeno uno dei due eventi. Scriveremo C = A È B (oppure A+B).

2.      INTERSEZIONE O PRODOTTO LOGICO fra due eventi A e B è quell’evento D che si verifica quando si verificano contemporaneamente i due eventi. Scriveremo D = A Ç B (oppure AB).

3.      NEGAZIONE di un evento A  è quell’evento E che si verifica quando non si verifica A. Scriveremo E =`A  oppure ~A (e leggeremo “non A”).

4.      INCLUSIONE o IMPLICAZIONE tra due eventi A e B: diremo che un evento A Í B (oppure A®B) se ogni volta che si verifica A si verifica anche B, e si dice anche che “A dipende logicamente da B”.

PROPRIETÀ

L’unione e l’intersezione tra eventi sono leggi di composizione interna nell’insieme I (insieme universo o spazio campione della prova) di tutti i possibili eventi relativi alla prova in oggetto. Esse godono delle proprietà:

1.      Associativa:   (A È B)ÈC = AÈ(B È C);  (A Ç B)ÇC = AÇ(B Ç C).

2.      Commutativa:  AÈB = BÈA;   A ÇB = BÇA.

3.      Distributiva:  AÇ(BÈ C) = (AÇB) È (AÇC);  AÈ(BÇ C) = (AÈB) Ç (AÈC).

4.      Idempotenza:    AÇA =A;  AÈA = A.

5.      Leggi di De Morgan: ~(AÈB) = ~BÇ~A; ~(A ÇB) = ~BÈ~A.                                    

AÈÆ=A;  AÇÆ=Æ;  AÈI=I;  AÇI=A;   A È`A =I;   A Ç`A=Æ;`Æ=I;  ~I=Æ; ~(~A)=A

DEFINIZIONI

1.      L’evento certo I è l’evento che si verifica sempre.

2.      L’evento impossibile f è quell’evento che non si verifica mai.

3.         Due eventi A e B si dicono INCOMPATIBILI quando non possono verificarsi contemporaneamente, cioè: A Ç B = Æ

4.      Due eventi A e B si dicono NECESSARI  quando almeno uno dei due deve presentarsi, cioè:

 A È B = I

Esempio 1.1

Nella prova “estrazione di un numero da un’urna che contiene palline numerate da 1 a 4” avremo:

E₁ ={esce il numero 1};E₂ ={esce il numero 2};E₃ ={esce il numero 3}; E₄ ={esce il numero 4};

I = { E₁; E₂; E₃; E₄ }.

Definiamo gli eventi:

A = { E₁; E₂; E₃ }  B = { E₂;  E₄} C = { E₁;E₃}  D = { E₄ }

Si ha, allora :
 AÈB=BÈC=I;       BÇC= Æ     AÇB={E₂}    `A= D     CÍ A     B Ç`A= { E₂;  E₄}=B

(AÈB)ÇC = { E₁; E₂; E₃; E₄ }Ç{ E_1; E₃ }={ E₁;E₃}.             

(AÇC)È(BÇC)={ E₁;E₃}ÈÆ={ E₁;E₃}.

`A  Ç`C ={ E₄}Ç{ E₂;E₄}={ E₄}.

DEFINIZIONE

Definiamo evento elementare E quell’evento per il quale si verifica che : AÇE=E   oppure  AÇE=Æ  "AÎI (cioè per ogni evento A o l’evento elementare è incluso in A oppure è con esso incompatibile).

Esempio 1.2

Si abbia un’urna che contiene 10 palline uguali in tutto tranne che nel colore: siano 3 bianche, % rosse, 2 nere. La prova consiste nell’estrazione di una singola pallina. Se indichiamo con:

B = viene estratta una pallina bianca;

R = viene estratta una pallina rossa;
N = viene estratta una pallina nera.

BÈR = “viene estratta una pallina bianca o rossa”

“pallina né bianca né rossa” = ~(BÇR)=~BÈ~R

Immaginiamo adesso, mediante la stessa urna di definire un’altra prova: “ estrazione di due palline consecutive” cioè senza rimettere nell’urna la pallina estratta per prima. Definiamo:

B₁ = “ la prima pallina estratta è bianca”

B₂ = “ la seconda pallina estratta è bianca”

R₁ = “ la prima pallina estratta è rossa” , e così via , R₂ , N_1,  N_2.

  B₁ Ç R₂ = “la prima pallina estratta è bianca e la seconda è rossa;

`B<sub>1</sub>Ç`B₁  = “nessuna delle due palline estratte è bianca”;

         R ₁Ç`R₂= “solo la prima pallina estratta è rossa”.

Rappresentiamo l’evento D = “Almeno una pallina estratta è bianca”

D = (B₁ Ç`B<sub>2</sub>) È (B<sub>2</sub> Ç`B₁) È (B₁ ÇB₂)

1.4 POSTULATI

Postulato 1:La probabilità di un evento A, che scriveremo P(A), è un numero non negativo: P(A)³0

Postulato 2: La probabilità dell’evento certo è sempre 1: P(I) =1

 Postulato 3: Se A e B sono eventi incompatibili, allora la probabilità della loro somma logica è la somma delle singole probabilità

( principio delle probabilità totali): AÇB=Æ Þ  R(AÈB)=R(A)+R(B)

Postulato 4: La probabilità dell’evento B dato che si è verificato l’evento A, la scriveremo P(B/A)è il rapporto fra la probabilità del contemporaneo verificarsi di A e B e la probabilità di A, se questa è diversa da zero( principio probabilità composte): P(A)¹0 Þ   R(B/A) =  R(AÇB)/P(A)                       

 È immediato constatare che i quattro postulati sono proprietà della frequenza relativa degli eventi (secondo i frequentisti) e del grado di fiducia connesso agli eventi ( secondo i soggettivisti).

Il pregio di questa assiomatizzazione risiede nell’esiguo numero di proposizioni poste a fondamento della teoria e, per contro, dell’enorme numero di teoremi che da queste si possono dimostrare.

1.5 TEOREMI

Teorema 1.1:   P(Æ)=0

Infatti:      IÈÆ=I  e  P(IÈÆ)= P(I) = 1  ( per il postulato 2)  ma si ha anche  IÇÆ=Æ, cioè i due eventi sono incompatibili, pertanto per il postulato3 si ottiene : P(IÈÆ)= P(I) +P(Æ)= 1+ P(Æ) da cui. 1=1+ P(Æ) Þ P(Æ)=0  (c.v.d.)

Teorema 1.2: P(`A)= 1 - P(A)

È noto che A  È`A = I   e che A e`A sono eventi incompatibili, pertanto per il postulato 3 si ha : R(A  È`A)=R(A)+R(`A),  d’altra parte P(AÈ`A)= P(I) = 1  quindi da R(A)+R(`A)=1 si trae la tesi.

Teorema 1.3: P(`AÇB) = P(B) - P(A ÇB)

Si ha:  B = BÇ I = BÇ (AÈ`A)= (B Ç A)È (BÇ`A)   essendo (B Ç A) e (BÇ`A) eventi incompatibili, sarà:

P(B) = P[(B Ç A)È (BÇ`A)] =P(B Ç A)+ P(BÇ`A) da cui la tesi.

Teorema 1.4: P(AÈ B) = P(A)+ P(B) - P( AÇB)

AÈB = A È (`AÇB)    dove  A  e `A Ç B  sono eventi incompatibili, quindi:

P(AÈB) = P[ A È (`AÇB)] = P(A) + P(`AÇB), ma per il teorema precedentemente dimostrato si che: P(AÈB) = P(A) + P(B) -P(AÇB). c.v.d.

QUEST’ULTIMO TEOREMA GENERALIZZA IL POSTULATO 3 AL CASO DI EVENTI NON INCOMPATIBILI.

EVENTI INDIPENDENTI STOCASTICAMENTE

DEFINIZIONE: Diremo che un evento B è indipendente da un evento A se il verificarsi di A non altera la probabilità che ha B di verificarsi. Formalmente: P( B/A) = P(B). Per cui dal quarto postulato deriva che:

Se due eventi A e B sono indipendenti allora:   P (AÇB) = P(A).P(B)

La probabilità del prodotto logico di due eventi indipendenti è uguale al prodotto delle singole probabilità

Le prove che generano eventi indipendenti si dicono indipendenti. Nella classe di prove costituite dall’estrazione di palline da un’urna si distinguono:

a)      Estrazioni con ripetizione (o estrazioni bernoulliane), quando ogni pallina estratta è rimessa nell’urna prima di procedere all’estrazione successiva.

b)      Estrazioni senza ripetizione quando le palline sono estratte in blocco ovvero non vengono rimesse nell’urna prima di procedere ad una nuova estrazione. In tal caso il risultato di ciascuna estrazione altera la probabilità delle estrazioni successive.

Attenzione: È importante  capire la differenza tra i concetti di incompatibilità e indipendenza stocastica. L’incompatibilità è una relazione tra eventi ed è rappresentabile per mezzo dei diagrammi di Eulero-Venn; invece l’indipendenza è una relazione che nasce dalla struttura delle prove, coinvolge esplicitamente la probabilità, non è rappresentabile per mezzo dei diagrammi di Venn.

1.6 LA MISURA DELLA PROBABILITÀ

Data una prova che genera  k eventi elementari E₁ E₂ ,…,E_k  necessari, incompatibili a due a due ed equiprobabili,

a)      E₁ÈE₂È … ÈE_k = I                      necessarietà;

b)      E_i ÇE_j  =Æ         per ogni i¹j           incompatibilità;

c)      P(E₁) = P(E₂) =…= P(E_k)               equiprobabilità.

per tale classe di eventi, dai postulati si deduce univocamente la misura della probabilità di ciascuno di essi. Infatti:

1 = P(I) =                                           (per il postulato 2)

= P(E₁ÈE₂È … ÈE_k ) =                    (perché eventi necessari)

= P(E₁)+P(E₂) + … +P(E_k ) =             (perché eventi incompatibili)

= k P( E_i )                                          (perché equiprobabili)

Quindi                                             

 k P( E_i ) = 1     da cui        P( E_i ) = 1/k     per ogni i =1,2,…,k                               

Pertanto se in una prova costituita da k eventi elementari, incompatibili, necessari ed equiprobabili, un evento A consiste di m eventi elementari, si ha cioè  A= E₁ÈE₂ È…È E_m ,allora si avrà: P(A)=P(E₁ÈE₂ È…È E_m )= P(E₁)+P(E₂)+… +P(E_m)=1/k+1/k+…+1/k= m/k.

Cioè:      P(A) = m/k

Se una prova consiste di k eventi elementari, incompatibili a due a due, necessari ed equiprobabili, allora la probabilità di un evento A è il rapporto tra i casi favorevoli al verificarsi di A (ovvero il numero di eventi elementari di cui si compone A) ed il numero dei casi possibili (ovvero il numero totale degli eventi  elementari della prova considerata)

Tale regola per il calcolo della probabilità di un evento A soddisfa i quattro postulati su cui è fondata la teoria, infatti:

1.      Il numero m/k ³0;

2.      Il numero dei casi favorevoli all’evento certo I è uguale al numero dei casi possibili, pertanto P(I)=1

3.      Se due eventi sono incompatibili, il numero di casi favorevoli all’unione è la somma dei casi favorevoli ai singoli eventi;

4.      La frazione dei casi favorevoli all’evento B/A è pari al rapporto fra i casi favorevoli ad A e B contemporaneamente, rispetto ai casi favorevoli al solo evento A.

Schema logico:

1)        Individuare correttamente la prova, quindi gli eventi elementari che la compongono verificando se sono necessari, incompatibili ed equiprobabili;

2)        Distinguere se gli eventi elementari consistono in un solo elemento (una faccia, una pallina, un numero) oppure consistono di più elementi (una coppia di facce, una terna di numeri)

3)        Esplicitare gli eventi più complessi come unione, intersezione o negazione degli eventi elementari sopra individuati;

4)        Per eventi incompatibili   AÇB=Æ Þ  R(AÈB)=R(A)+R(B)

       Per eventi compatibili     AÇB¹Æ Þ  R(AÈB)=R(A)+R(B)- P(AÇB)

5)        Per eventi indipendenti  Þ P(AÇB) = P(A).P(B)

Per eventi dipendenti     Þ P(AÇB) = P(A).P(B/A)

Esempio 1.3

Un’urna contiene 15 palline di cui 3 bianche, 5 nere e 7 rosse.

a)      Si estrae una sola pallina: qual è la probabilità che sia rossa? Oppure non nera?

b)      Si estraggono due palline con ripetizione: qual è la probabilità di estrarre due palline bianche? Una bianca e una rossa? Due palline non nere? Almeno una bianca?

c)      Si estraggono due palline senza ripetizione: quali sono le probabilità degli eventi descritti alla lettera b)?

Risposte.

a)      Ogni pallina ha probabilità 1/(3+5+7)=1/15=0,06667 di essere estratta. Pertanto, indicando con R l’evento: “esce una pallina rossa”, B: ”esce una p. bianca”, N: “esce una p. nera”, si avrà:
P(R)=7/15=0,46667;    P(`N )= 1-P (N) =1-5/15 = 2/3 =0,66667.

b)      L’estrazione con ripetizione dà luogo ad eventi indipendenti, perché la composizione dell’urna rimane la stessa dopo la prima estrazione, pertanto non si modificano le probabilità degli eventi di cui ci occupiamo. Definiamo B₁ = “alla prima estrazione esce una pallina bianca”, B₂ = ”alla seconda estrazione esce una pallina bianca”, e così via per gli eventi R₁ R₂ N₁ N₂ . Si ha:

P(B₁ )= P(B₂ )= 3/15;   P(N₁ )= P(N₂ )=5/15;   P(R₁)=P(R₂)=7/15.                 

P( estrazione due palline bianche)=P(B₁ ÇB₂ )= P(B₁ )P(B₂ )=(3/15)(3/15)=1/25=0,04= 4% ;                                                                                                                                                                                               

P(estrazione una bianca e una rossa)= P[(B₁ ÇR₂) È (R₁ ÇB₂)]= P(B₁ )P(R₂)+ P(B₂ )P(R₁)= 14/75                                                                 

P(estrazione due palline non nere)= P(`N<sub>1</sub> Ç`N₂ )= P(`N<sub>1</sub>) P(`N₂ )=4/9;

P(almeno una bianca) = P[(B₁ Ç`B<sub>2</sub>) È (B<sub>2</sub> Ç`B₁) È (B₁ ÇB₂)]= P(B₁)P(`B<sub>2</sub>)+P(B<sub>2</sub>)P(`B₁)+ +P(B₁)P(B₂) = 3/15(1-3/15)+3/15(1-3/15)+ (3/15)(3/15)=9/25

c)      L’estrazione senza ripetizione dà luogo ad eventi dipendenti, pertanto mentre rimangono invariate le probabilità relative alla prima estrazione, nella seconda estrazione si modifica no le probabilità in funzione degli eventi che si sono verificati precedentemente.

P(estrazione due palline bianche)=P(B₁ÇB₂)=P(B₁)P(B₂ /B₁)=(3/15)(2/14)=1/35=0,02857=2,857%                                                                                                                                                                                               

P(estrazione una bianca e una rossa)= P[(B₁ÇR₂)È(R₁ ÇB₂)]= P(B₁)P(R₂/B₁)+P(R₁)P(B₂/R₁)=1/5;                                                                 

P(estrazione due palline non nere)= P(`N<sub>1</sub> Ç`N₂ )= P(`N<sub>1</sub>) P(`N₂ / `N₁)=90/210=0,42857;

P(almeno una bianca) = P[(B₁Ç`B<sub>2</sub>)È(`B₁Ç B₂)È(B₁ ÇB₂)] =P(B₁)P(`B<sub>2</sub> / B<sub>1</sub>)+P(`B₁)P(B₂/ `B₁) + +P(B₁)P(B₂/ B₁) = 3/15(12/14)+ (1-3/15) 3/14+ (3/15)(2/14)=13/35=0,37143.

1.7 TEOREMA DI BAYES

Siano H₁,H₂,…, H_k una successione di eventi necessari, cioè H₁ÈH₂È … ÈH_k = I   e incompatibili               

H_i ÇH_j  = Æ  per ogni i¹j , e sia E un evento incluso nello stesso spazio campione, EÌ I , si avrà allora:  

E = EÇI=E Ç(H₁ÈH₂È … ÈH_k ) = (EÇH₁) È (EÇH₂) È…È(EÇH_k)   dove  (EÇH₁), (EÇH₂), …(EÇH_k) sono eventi a due, a due incompatibili, pertanto:

P(E) = P(EÇH₁)+P(EÇH₂)+ …+P(EÇH_k). 

Per il postulato 4 si ha:

 (*) P(H_i/E)=   per i=1,2,…,k  ed anche:

P(E/H_i)=   per i=1,2,…,k ,da cui:   P(H_iÇE)= P(E/H_i)P(H_i),pertanto:

Sostituendo nella (*) si ha la formula di Bayes:

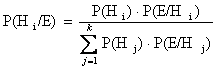
Il numeratore della frazione rappresenta la probabilità che si presenti la causa H_i e che in dipendenza da ciò si verifichi E, il denominatore esprime invece la probabilità che si verifichi E non importa per quale causa.

Se sappiamo dunque che un evento E può essere stato originato da un certo numero di cause H₁,H₂,…, H_k tra loro incompatibili, il teorema di Bayes ci consente di calcolare la probabilità che E sia stato originato dall’evento H_i.

Esempio1.7.1:

In una certa fabbrica esiste la probabilità pari ad 1/3 di contrarre la malattia H. Un operaio avverte un sintomo A (per esempio mal di testa) che può essere dovuto alla malattia H, sia ad altra causa `H. La probabilità di avere il sintomo A quando si ha la malattia H è pari al 90%,mentre nel caso che non si abbia la malattia H, il sintomo si presenta con probabilità del 6%.

Qual è la probabilità che, se un operaio ha il sintomo A, questo sia stato causato dall’aver contratto la malattia H?

P(H)=1/3    P() = 2/3 P(A/H) = 0,9    P(A/) =0,06 

P(H/A) =   (1/3)0,9/[ (1/3)0,9+(2/3)0,06]»0,12

FORMULA DI BAYES:

ESERCIZI :

1) Consideriamo due scatole: nella prima sono contenute  1 pallina rossa e 1 pallina bianca, nella seconda 3 palline rosse e 1 pallina nera. Supponiamo ora che, scelta a caso una scatola, si estragga una pallina e supponiamo che la pallina estratta sia rossa; ci si chiede qual è la probabilità che essa provenga dalla prima scatola.

Sia H₁:"la pallina è stata estratta dalla prima scatola", H₂:"la pallina è stata estratta dalla seconda scatola" e A:" la pallina estratta è rossa".

Si ha:   p(H₁)= p(H₂)=1/2;   p(A/ H₁)=1/2;   p(A/ H₂)=3/4;   

p(H₁/A)=(1/2∙1/2)/ (1/2∙1/2+1/2∙3/4)= 2/5.

2) Un'azienda dispone di tre macchine che sono in grado di filettare, per ogni ora, 100 viti del medesimo tipo, in particolare:

·        la macchina 1 filetta 50 viti all'ora e la probabilità che origini viti difettose è 0,08

·        la macchina 2 filetta 30 viti all'ora e la probabilità che origini viti difettose è 0,06

·        la macchina 3 filetta 20 viti all'ora e la probabilità che origini viti difettose è 0,05.

Alla fine di un'ora si estrae a caso una vite che risulta difettosa. Si vuole conoscere la probabilità che essa sia stata prodotta dalla macchina 2.

H_i = macchina i ,    con i=1,2,3     D= vite difettosa. 

 p(H₂/D)= (0,3∙0,06)/ (0,5∙0,08+0,3∙0,06+0,2∙0,05)=0,2647

E' facile provare che:   p(H₁/D)+ p(H₂/D)+ p(H₃/D) = 1

3) In una classe il 25% degli studenti è insufficiente in matematica, il 15% in italiano e il 10% sia in matematica che in italiano. Scegliendo a caso uno studente:

a)      Se è insufficiente in italiano, qual è la probabilità che lo sia in matematica?    [2/3]

b)      Se è insufficiente in matematica, qual è la probabilità che lo sia in italiano?    [2/5]

c)      Qual è la probabilità che sia insufficiente in italiano o in matematica?           [3/10]

4) La probabilità che un uomo viva altri 10 anni è 1/4 e la probabilità che sua moglie viva altri 10 anni è 1/3. Determinare la probabilità che:

a)      Entrambi siano vivi tra 10 anni;                                                                     [1/12]

b)      Almeno uno dei due sia vivo tra 10 anni;                                                       [1/2]

c)      Né l'uno né l'altra siano vivi tra 10 anni;                                                                    [1/2]

d)      Soltanto la moglie sia viva tra 10 anni.                                                           [1/4]

5) Due tiratori aprono il fuoco simultaneamente. La probabilità di un colpo a segno del primo tiratore è uguale a p₁ ; quella del secondo tiratore a p₂. Qual è la probabilità che uno dei due tiratori colpisca il bersaglio mentre l'altro lo manca?

                                                                                         [p₁ +p₂ -2p₁p₂]

6) Un'urna contiene 6 palline:1 bianca, 2 rosse e 3 azzurre; un'altra ne contiene 12: 2 bianche, 6 rosse e 4 azzurre. Si estrae una pallina da ciascun'urna. Qual è la probabilità di non estrarre una pallina azzurra?                                                                                            [1/3]

7)Tre urne assolutamente identiche contengono: la prima 20 palline bianche, la seconda 10 bianche e 10 nere, la terza 20 nere. Si sceglie un'urna a caso e si estrae una pallina bianca. Calcolare la probabilità che la pallina sia stata estratta dalla prima urna.                                                                                                 [2/3]

8) In una scuola il 4% dei maschi e l'1% delle femmine sono più alti di m1,80. Inoltre il 40% degli studenti sono maschi. Ora, se uno studente è scelto a caso ed è più alto di m1,80, qual è la probabilità che sia femmina?                         [3/11]

9) Il montaggio del 30% di apparecchi di una fabbrica è fatto da uno specialista altamente qualificato e quello del 70% da uno di qualifica media. L'affidabilità del funzionamento dell'apparecchio è di 0,9 nel caso in cui il montaggio sia stato effettuato dallo specialista altamente qualificato, e di 0,8 se è stato effettuato dal secondo specialista. Un apparecchio scelto a caso è risultato di funzionamento affidabile. Determinare la probabilità che il suo montaggio sia stato effettuato dallo specialista altamente qualificato.                                                       [0,325]

2.Teoria delle variabili casuali

Una variabile casuale (vc) è una funzione reale definita sullo spazio campione che associa ad ogni evento un numero reale.

Per esempio, se nella prova “lancio di un dado” ai sei possibili eventi “faccia con 1 puntino”, “faccia con 2 puntini”, ecc. facciamo ordinatamente corrispondere l’insieme dei numeri reali 1,2,…,6, abbiamo definito la vc che assume  i valori 1,2,…,6 in corrispondenza ai sei eventi.

E’ bene sottolineare come la corrispondenza tra eventi e numeri reali creata dalla vc non è necessariamente biunivoca.

Esempio 2.1:

Tre monete ben bilanciate vengono lanciate contemporaneamente. Lo spazio campione è costituito dai seguenti eventi elementari:

E₁=TÇTÇT      E₂=TÇTÇC       E₃=TÇCÇT      E₄=CÇTÇT    E₅=TÇCÇC  

E₆=CÇTÇC      E₇=CÇCÇT       E₈=CÇCÇC

La probabilità di ciascun evento è 1/8.

Definiamo la vc X=numero delle facce Testa nel lancio di tre monete.

La vc può assumere il valore 0 (se non si presenta nessuna testa),1 (se si presenta una sola testa),2 (se si presentano due teste), 3 (se tutte e tre le monete presentano la faccia testa).

Il calcolo delle probabilità è immediato. Ad esempio:

P(X=2)=P(E₂È E₃È E₄)=P(E₂)+P(E₃)+P(E₄)=1/8+1/8+1/8=3/8, e così via.

La tabella consente di calcolare la probabilità di certi eventi: per esempio “la probabilità che esca più di una testa”:

P(X>1)=P[(X=2) È(X=3)]=P(X=2)+P(X=3)=3/8+1/8=1/2,  ovvero

P(X>1)=P[~(X £ 1)]=1- P(X £ 1)=1-(1/8+3/8)=1/2.

2.1 VARIABILI CASUALI DISCRETE.

Una variabile casuale si definisce variabile casuale discreta  se può assumere un numero finito o al più numerabile di valori.

Si definisce variabile casuale continua  quella che assume valori compresi in un intervallo reale.

Una vc discreta è nota se è nota la sua distribuzione di probabilità, ovvero se si conoscono i valori che può assumere assieme alle rispettive probabilità.

Esempio 2.2:

Si lanciano due dadi uguali; studiare la vc definita come la somma dei punti che si presentano sulle due facce.

La X è una vc discreta ben definita perché  p_i ³ 0"i  e inoltre S p_i=1.

Tramite la distribuzione della vc si può calcolare la probabilità di qualsiasi evento. Per esmpio:

P(X £ 4)= P(X=2)+P(X=3)+P(X=4)=1/36+2/36+3/36=1/6;

P(0 £ X<6) =P(X=2)+P(X=3)+P(X=4)+P(X=5)=10/36=5/18;

Esempio 2.3:

Sia T la vc definita come “il numero di lanci necessari finché non si verifichi testa” in una successione di prove di lanci di una moneta per la quale è p la probabilità che si verifichi testa e q=1-p la probabilità che si verifichi croce.

Tale vc assume il valore 1 (se si verifica testa al primo lancio) con probabilità p, assume il valore 2 (se si verifica testa al secondo lancio) con probabilità (1-p)p; e così via.

Questa vc è una variabile aleatoria discreta numerabile ben definita perché   p_i ³ 0   "i  e inoltre:

 Calcoliamo alcune probabilità, ad esempio:

P(T=4)=p(1-p)³

P(T  ³ 3)=1-P(T < 3)=1-[p + p(1-p)]=(1-p)²

P(T=pari)=SP(T=2i)= Sp(1-p) ^2i-1=

                                                    1

  P(T=dispari)= 1-P(T=pari)= ¾¾¾

                                                   2-p                  

Le quali risultano uguali solo per p=0 ovvero mai.

In generale, essendo p>0 sarà sempre P(T=dispari)>P(T=pari).

2.2 VARIABILI CASUALI CONTINUE.

Per le vc continue non è possibile elencare i valori che esse assumono e quindi attribuire a ciascuno di essi la rispettiva probabilità, come si è fatto per le vc discrete.

Diremo che una variabile casuale continua  che assume valori in un certo intervallo (a,b), che può essere anche l’intera retta reale, è ben definita quando esiste una funzione f(x), detta funzione di densità tale che per ogni x₀ Î(a,b), si abbia:

                       P(x₀ £ X < x₀ +dx)= f(x₀ )dx

Tramite la definizione e nota la funzione di densità, si possono calcolare le probabilità di quasivoglia evento utilizzando le nozioni elementari del calcolo integrale.

Naturalmente affinché la definizione sia in accordo con i postulati occorre e basta che la funzione di densità sia  non negativa e inoltre l'area totale della f(x) sul campo di definizione sia pari a1, poiché l'evento certo ha probabilità 1.

Cioè:

È usuale assumere che ogni vc continua sia definita nell'intervallo (-¥,+¥) con la convevzione che la funzione di densità sia nulla per quei valori esterni all'intervallo di definizione.

Dalla definizione discendono alcune importanti conseguenze: per esempio la probabilità che una vc X continua asssuma un qualunque valore x₀ è sempre zero:

FUNZIONE DI RIPARTIZIONE

Definiamo funzione di ripartizione di una vc  la funzione:

Dalla definizione segue che:

F'(X) = f(x)

dF(X) = f(x)dx

P(a £ X < b) = F(b) - F(a)

Esempi:

1)      Una vc X ha come funzione di densità:

determinare la funzione di ripartizione  e la probabilità P(1<X<2)

VARIABILI ALEATORIE O CASUALI DISCRETE

VALORE MEDIO

VALORE MEDIO di una vc al quadrato  M(X²)

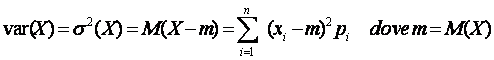
VARIANZA

FORMULA PRATICA PER IL CALCOLO DELLA VARIANZA

SCARTO QUADRATICO MEDIO

VARIABILI CASUALI CONTINUE

Sia X una vc continua che assume tutti i valori compresi nell'intervallo [a,b] e sia f(x) la sua funzione di densità.

VALORE MEDIO O SPERANZA MATEMATICA

VALORE MEDIO di una vc al quadrato 

M(X²)=

La varianza è definita allo stesso modo della vc discreta e vale anche per le vc continue la formula pratica per il calcolo della varianza.

La moda  di una vc continua è quel valore a cui corrisponde la massima densità di probabilità.

La mediana è quel valore al quale corrisponde per la funzione di ripartizione il valore 1/2.

DISTRIBUZIONI TIPICHE DI PROBABILITÀ

VARIABILI ALEATORIE DISCRETE

IL PROBLEMA DELLE PROVE RIPETUTE E LA VARIABILE CASUALE CON DISTRIBUZIONE BINOMIALE

Lanciando un dado 5 volte di seguito, che probabilità c’è che esca 3 VOLTE la faccia “1”?

L’evento può verificarsi in molte modalità diverse: ad esempio, si verifica qualora “1” esca ai primi 3 lanci, e poi non esca più ai successivi 2 lanci;  oppure, si verifica qualora “1” esca esclusivamente agli ultimi 3 lanci (ma non esca ai primi 2); oppure ancora, si verifica qualora “1” esca al secondo, al terzo e al quinto lancio, ma non agli altri lanci;  ecc. ecc.

Fissiamo la nostra attenzione su UNA di queste modalità.

Ad esempio:  lanciando un dado 5 volte di seguito, che probabilità c’è che la faccia “1” esca ai primi 3 lanci (e poi non esca più)?

Tenendo conto del fatto che l’esito di un lancio non è condizionato in alcun modo dall’esito del lancio precedente, abbiamo: p(1Ù1Ù1Ùnon1Ùnon1) = p(esce 1 al 1° lancio)× p(esce 1 al 2° lancio)× p(esce 1 al 3° lancio)× p(non esce 1 al 4° lancio)× p(non esce 1 al 5° lancio)  = =

Consideriamo ora UN’ALTRA fra le possibili modalità. 

Ad esempio, lanciando un dado 5 volte di seguito, che probabilità c’è che la faccia “1” esca esclusivamente agli ultimi 3 lanci (ma non esca ai primi 2)?

Abbiamo: p(non1Ùnon1Ù1Ù1Ù1) = p(non esce 1 al 1° lancio)× p(non esce 1 al 2° lancio)× p(esce 1 al 3° lancio)× p(esce 1 al 4° lancio)× p(esce 1 al 5° lancio) = = ,  ...e così via,...

Allora CIASCUNA delle tante modalità con cui si può verificare l’evento “esce 3 VOLTE la faccia 1” ha probabilità data dal prodotto

Ora, in virtù del teorema sulle probabilità totali per eventi indipendenti, abbiamo: p(esce 3 volte la faccia 1) =

= p( (1 esce le prime 3 volte)Ú (1 esce le ultime3 volte)Ú (1 esce la 2^a, la 3^a e la 5^a volta)Ú ...) =

= +++....

Questi addendi sono tanti quante le modalità con cui l’evento “esce 3 volte la faccia 1” si può presentare, cioè tanti  quanti sono i modi in cui, sui 5 lanci, possiamo fissare quei 3 nei quali immaginiamo esca “1”.

Tra 5 oggetti (nel nostro caso i 5 lanci) ne possiamo selezionare 3(nel nostro caso quei 3 lanci in cui compare la faccia 1) in  modi ( sono le combinazioni di 5 oggetti di classe 3, C_5,3).

Dunque avremo: p(esce 3 volte la faccia 1) =

Generalizzazione

Supponiamo che un evento E sia ripetibile e facciamo con esso n prove, sempre nelle medesime condizioni. Indichiamo con p la probabilità che in una prova si presenti E ( successo), e con q=1-p la probabilità dell'evento non E. Indicando con p_n,k la probabilità che l'evento E si presenti k volte nelle n prove, si ha:

La vc S "numero di successi in n prove" assume i valori:

È da notare che la somma delle probabilità è uguale a (p+q)ⁿ=1

Si dimostra  che:

LO SCHEMA TESTA CROCE

Se si pone E = non E, cioè p = q =1/2, si ha:

VARIABILE CASUALE CON DISTRIBUZIONE GAUSSIANA.

È la variabile casuale che assume qualsiasi valore reale e la cui funzione di densità, che indichiamo con il simbolo f(x), è definita come segue:

dove m è il valore medio, s è lo scarto quadratico medio e s² è la varianza.

Come si vede la funzione densità dipende dai due valori m e  s ed ha le seguenti caratteristiche:

à  Assume il massimo valore in corrispondenza della media m;

à  Presenta due punti di flesso in corrispondenza dei valori m-s e m+s ;

à  È asintotica rispetto all’asse delle ascisse.

In particolare per   m=0     e       s²=1    si ha:

che si chiama:

VARIABILE CASUALE GAUSSIANA STANDARDIZZATA O NORMALE:

pertanto:

à  Assume il valore massimo in corrispondenza di x=m=0;

à  presenta i due punti di flesso in corrispondenza dei valori -1 e +1;

à  È simmetrica rispetto all’asse y ( è una funzione pari).

ESERCITAZIONE DI LABORATORIO.

1)      Calcolare mediante il foglio elettronico i valori della distribuzione normale e rappresentarla graficamente.

Per calcolare i valori della colonna B (f(x) o probabilità) occorre utilizzare le funzioni EXP( ) che calcola il valore del numero di nepero elevato all’argomento posto tra parentesi tonde; e la funzione radq.pi ( ) che calcola la radice quadrata del numero p moltiplicato con il valore posto entro parentesi.

VARIABILE CASUALE CON DISTRIBUZIONE POISSONIANA

Consideriamo la vc X che assume i valori interi non negativi: 0, 1, 2, 3,…., k,….. Indichiamo con:

la probabilità che X assuma un generico valore kÎN, dove l è una costante positiva ed e~2,71828 è il valore approssimato della base dei logaritmi neperiani.

Si può dimostrare che:

p₁+ p₂+ p₃+…+ p_k+…=1

Si dimostra inoltre che: