Scheda successiva   

MODELLO DI POINCARE' (1854-1912)

CON IL MENU IPERBOLICO DI CABRI II

            La teoria è consistente con gli assiomi della geometria iperbolica pertanto la conica orizzonte rappresenta un modello del piano non-euclideo di tipo iperbolico.

 Tra questi assiomi uno stabilisce che dati due h-punti distinti esiste una sola retta passante per essi. Non è difficile convincersi della validità di questo assioma in relazione alla scelta fatta della tipologia delle rette. Un secondo assioma della geometria iperbolica afferma che:  Ogni segmento può essere prolungato. Questo assioma è soddisfatto anche se il modello del disco è limitato. Infatti le h-rette sono topologicamente aperte per cui i punti ad esse appartenenti possono avvicinarsi a piacere a C senza tuttavia giacere su C. In altri termini fissato su una h-retta un h-punto "vicino" a C è sempre possibile determinare un ulteriore h-punto sulla retta "più vicino" a C del precedente.

h-distanza: Siano P e Q due punti.  Essi individuano univocamente una h-retta che, al limite, interseca C in due punti euclidei A e B .  Facciamo notare che A e B non sono h-punti in quanto appartengono a C. Siano |PA|, |PB|, |QA|, e |QB| le distanze euclidee P da A, ecc. e sia ln il logaritmo naturale.  Allora definiamo la h-distanza tra i punti P e Q come: d(PQ) = |ln (|PA|/ |PB|)/(|QA|/ |QB|)|  cioè il logaritmo naturale del birapporto PQAB.

Nel modello la distanza così definita gode delle seguenti proprietà generali:

     la distanza d(PQ) è definita per ogni coppia di punti P e Q.

d(PQ) = 0 se e solo se P e Q  coincidono altrimenti la distanza è positiva.

d(PQ) = d(QP) ossia la h-distanza di P da Q è uguale alla h-distanza di Q da P.

     Una linea retta individua il cammino di lunghezza minima tra i punti due punti che la individuano. In altri termini vale la "disuguaglianza triangolare"   d(AC) <= d(AB) + d(BC), dove A, B e C  sono tre punti qualsiasi.

     La distanza è continua e fissato un qualsiasi numero positivo x esiste almeno una coppia di punti  P e Q tali che d(PQ) = x.  Ciò in accordo con l'assioma che afferma:  "Si possono costruire circonferenze di qualsiasi centro e raggio".

Una dimostrazione del fatto che la distanza scelta soddisfa tutte le precedenti proprietà può essere trovata in  E.E. Moise's "Elementary Geometry from an Advanced Standpoint" [Moise-74].

h-circonferenze: una h-circonferenza è definita come il luogo dei punti del piano iperbolico equi h-distanti da un h-punto fissato.

h-ampiezza di un h-angolo: consideriamo l'angolo di figura 1. Le rette BA' e BC' sono tangenti (in senso euclideo) agli archi AB e BC. Per definizione la h-ampiezza dell'angolo iperbolico coincide con l'ampiezza euclidea dell'angolo formato dalle rette tangenti BA' e BC'.

Per usare il menu iperbolico, creato da J.M.Laborde, occorre cliccare su File, Apri, e scegliere come Tipo file: file di un menu (*.MEN). Comparirà un'icona dal nome Iperbolica su cui si dovrà cliccare due volte. In questo modo sulla barra degli strumenti si sono aggiunte delle icone nuove, con costruzioni i cui nomi sono preceduti dall’aggettivo iperbolico. Le usuali icone del cabri II plus si trovano sulla destra.

Per iniziare la costruzione del modello di Poincarè occorre disegnare il piano iperbolico (secondo pulsante Orizzonte del piano iperbolico di poincare)) dopodiché ogni volta che si disegna una figura iperbolica bisogna sempre indicare rispetto a quale orizzonte si lavora. ( se vuoi un aiuto premi F1)

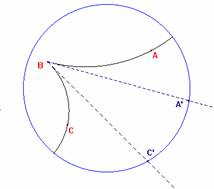
Prova a disegnare una retta iperbolica  AB (Terzo pulsante  ) , poi manipola la retta AB fino a farla passare per il centro O di orizzonte. Cosa succede?………………………..

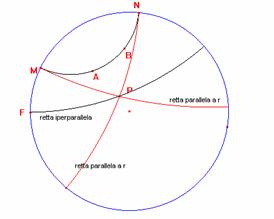 Disegnata una retta iperbolica AB e un punto P fuori di essa, per P passano infinite rette che non incontrano AB, in particolare esistono due rette che separano le rette incidenti la retta AB da quelle non incidenti (o iperparallele).

La situazione è analoga a quella che si ha nel fascio di rette passanti per il centro di un'iperbole, dove gli asintoti separano le rette secanti                       all'iperbole da quelle che non intersecano l'iperbole.

Le rette del modello, dunque, rispetto alla relazione di incidenza possono essere:

secanti (l'intersezione è un punto del disco orizzonte),

parallele (l'intersezione è un punto della circonferenza),

 iperparallele o non incidenti (l'intersezione è vuota).

Proviamo a verificare come in questo modello risultino veri i teoremi di Euclide dimostrati senza far uso del Quinto Postulato, e invece non valgano quelli che ne fanno uso.

RETTE PARALLELE TAGLIATE DA UNA TRASVERSALE FORMANO ANGOLI ALTERNI INTERNI CONGRUENTI, …(proposizione 29 dimostrata con il V postulato)

1.       Disegna la circonferenza orizzonte (secondo pulsante da sinistra)

2.       Disegna due rette iperboliche asintoticamente parallele (che abbiano in comune il punto di intersezione con orizzonte)

3.       Segna un punto R sulla prima e un punto S sulla seconda retta (secondo pulsante Punto su un oggetto)

4.       Disegna una retta iperbolica che passi per R e S

5.       Misura gli angoli alterni interni formati dalle due rette parallele con la trasversale (sesto pulsante Ampiezza iperbolica: occorre indicare tre punti, il secondo dei quali è il vertice)

6.       Manipola la figura e fai le tue osservazioni.

Con la stessa costruzione puoi verificare la validità del TEOREMA DELL'ANGOLO ESTERNO, dimostrato da E. senza far uso del V postulato.

SOMMA DEGLI ANGOLI INTERNI DI UN TRIANGOLO

1.       Disegna la circonferenza orizzonte

2.       Disegna un triangolo iperbolico i cui vertici chiama A, B e C

3.       Misura ciascuno dei tre angoli interni

4.       Muovendo i vertici del triangolo noterai che la somma dei tre angoli è sempre inferiore a 180°

5.       Cosa succede se i vertici del triangolo toccano la circonferenza orizzonte?

………………………………………………………………………