L'INVERSIONE CIRCOLARE

Potrei esser rinchiuso in un guscio di noce,

eppur sentirmi re di sconfinati spazi.

William Shakespeare (1564-1616),

Amleto, Atto II, Scena 2.

Dato un punto P(x, y), non coincidente con l’origine degli assi cartesiani, il punto P’(x’, y’) deve appartenere alla semiretta di origine O e passante per P. Quindi il punto P’ deve avere coordinate (kx, ky) per un certo numero reale k positivo.

Supponendo che il raggio della circonferenza sia 1, si ha:

.

Si ha quindi:

ovvero:

.

Ne segue che:

.

Quindi il punto P’ ha coordinate: Quindi il punto P’ ha coordinate:

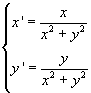
In generale, per una circonferenza di raggio di inversione r, si ottiene:

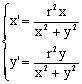
Quest’ultima relazione vale per tutti i punti del piano tranne che per l’origine.

 

• L'inversione è una involuzione: se P' = I(P) tramite una inversione I, allora P = I(P'). In altre parole, componendo I con se stessa si ottiene la funzione identità. Quindi l'inversione I è una corrispondenza biunivoca  (aggiungendo al piano il punto all'infinito) e coincide con la sua funzione inversa I ^{− 1}.
• La composizione di inversioni non è mai una inversione. La composizione di due inversioni aventi lo stesso centro è una omotetia con quel centro

In ambiente CABRI II esiste una Macro chiamata Inversione circolare, che disegna un punto corrispondente di un  altro rispetto a una circonferenza.

Vediamo con Cabri come varia il punto P' immagine di P in un'inversione circolare.

1.      Disegna una circonferenza (quarto pulsante circonferenza) che chiameremo inv di centro O (penultimo pulsante nomi);

2.      Disegna un punto fuori da inv (secondo pulsante) che chiameremo P;

3.      Disegna la retta OP (terzo pulsante);

4.      Costruisci l'immagine P' di P mediante l'inversione circolare (sesto pulsante inversione); (premi il tasto F1 per avere istruzioni )

5.      Muovi il punto P. Cosa succede alla sua immagine P'?

Quando P è interno a inv …………………quando P si allontana da O..……………..

Quando P è esterno a inv…………………quando P si avvicina ad O………………..

Quando P sta sulla circonferenza inv ………..

Qual è l'immagine del punto O?………………………………..

Dalla definizione (*) segue che:

CONCLUSIONE:

à     Ciascun punto interno alla circonferenza d'inversione si trasforma in un punto ad essa esterno, e viceversa. Quindi possiamo considerare il cerchio come un concentrato, un microcosmo della parte di piano ad esso esterno.

à     Il punto O ha per immagine tutti i punti della retta impropria del piano.

Un'altra caratteristica dell'inversione è di essere una corrispondenza involutoria cioè coincide con la sua inversa, pertanto se P è l'immagine di P' allora P' sarà l'immagine di P.

à     La circonferenza inv è luogo di punti uniti e quindi unita.

à     Ogni retta passante per O è unita ma non luogo di punti uniti: i punti di essa che sono interni a inv  si trasformano nei punti che sono esterni e viceversa.

Costruiamo adesso l'immagine di una retta che non passa per il centro O.

1)      Disegna una retta r non passante per O ed esterna alla circonferenza inv;

2)      disegna un punto P su r (secondo pulsante punto su un oggetto);

3)      crea l'immagine P' di P mediante l'inversione rispetto a inv;

4)      Seleziona lo strumento traccia (penultimo pulsante) e clicca su P';

5)      muovi il punto P su r: cosa descrive la sua immagine P'?……………………………

6)      cancella la traccia e seleziona luogo dal quinto pulsante, indicando prima il punto P' e poi il punto P: verrà costruito il luogo immagine della retta r.

7)      sposta la retta r in modo che sia tangente a inv e poi secante e ripeti le operazioni di sopra.Cosa succede?......................................................................................

CONCLUSIONE:

à     Le rette non passanti per O si mutano in circonferenze passanti per O, e viceversa.

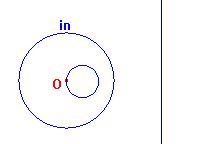
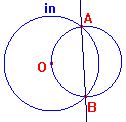
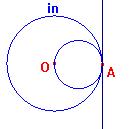
Fig.1

Nella figura di sopra vediamo i tre casi che si possono presentare:

se la retta è esterna a inv la sua immagine è contenuta in inv, se è tangente a inv in A anche l'immagine sarà tangente internamente in A; se è secante in A e in B, anche l'immagine secherà inv negli stessi punti (che sono uniti).

Qual è l'immagine di un cerchio non passante per O?

1)      Disegna una circonferenza c non passante per O ed esterna alla circonferenza inv;

2)      disegna un punto P su c (secondo pulsante punto su un oggetto);

3)      crea l'immagine P' di P mediante l'inversione rispetto a inv;

4)      seleziona lo strumento traccia (penultimo pulsante) e clicca su P';

5)      muovi il punto P su c: cosa descrive la sua immagine P'?……………………………

6)      cancella la traccia e seleziona luogo dal quinto pulsante, indicando prima il punto P' e poi il punto P: verrà costruito il luogo immagine della circonferenza c.

7)      sposta c in modo che sia tangente a inv e poi secante.

8)      Cosa succede quando c passa per il centro 0 dell’inversione?......................................

CONCLUSIONE:

à     una circonferenza non passante per il centro O d'inversione si muta in………………… ……………………………………………………………………………………………una circonferenza passante per O.......................................................................……..

ELEMENTI UNITI

PUNTI UNITI:   tutti i punti della circonferenza inv base dell'inversione circolare

RETTE UNITE:  tutte le rette passanti per O centro dell'inversione circolare

CIRCONFERENZE UNITE:

La circonferenza inv, essendo luogo di punti uniti è unita.

Esistono altre circonferenze unite?

1)      Disegna la circonferenza inv di centro O;

2)      Disegna una circonferenza c di centro O';

3)      Costruisci i punti A e B = inv Ç c;

4)      Individua un punto P su c e disegna inv(P) = P'; inv(A) =……; inv(B) =…….;

5)      Muovi c con il mouse (cliccando su O' per traslare la circonferenza, sulla circonferenza stessa per far variare il suo raggio), fino a quando P' Îc (la circonferenza c è unita quando inv(P)Îc "PÎc);

6)      Fissa un altro punto Q sulla circonferenza, fanne il corrispondente mediante l'inversione: anche inv(Q) Îc, confermando che la c è unita;

7)      Traccia la semiretta OA e il segmento O'A: OA e O'A sono…………………………. OA è dunque ………………………………alla c;

La circonferenza C si dice ortogonale a inv  ed è unita.

DUE CERCHI SI DICONO ORTOGONALI  QUANDO SONO ORTOGONALI LE RISPETTIVE TANGENTI NEI PUNTI DI INTERSEZIONE

Dalla definizione si può dedurre che:

1)      I punti di intersezione di due cerchi ortogonali si ottengono intersecando uno di essi con il cerchio che ha per diametro il segmento che unisce i loro centri. Infatti (vedi fig.1), i triangoli OAO' e OBO' sono rettangoli per la definizione di cerchi ortogonali, essendo i loro cateti raggio di un cerchio e tangente dell'altro, ed hanno l'ipotenusa coincidente, allora devono avere i vertici sul cerchio che ha per centro M punto medio di OO' e diametro OO'

2)     

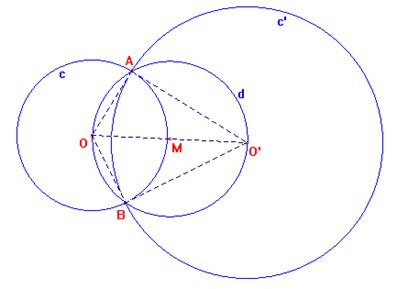
fig.1

Esercizi
1. Determinare l’inverso di un quadrato tangente al cerchio di inversione.

2. Trovare l’immagine del punto P(3; -1) nella inversione circolare rispetto alla circonferenza unitaria di centro l’origine degli assi.

3. Determinare l’immagine del punto P(1, 4) nell’inversione circolare rispetto alla circonferenza di centro l’origine degli assi e raggio 2.
4. Determinare l’immagine del punto P nell’inversione circolare rispetto alla circonferenza di centro l’origine degli assi e raggio 1.

5. Determinare l’immagine tramite l’inversione rispetto alla circonferenza goniometrica della retta .

6. Determinare l’immagine tramite l’inversione circolare rispetto alla circonferenza goniometrica della retta y = x (attenzione al punto O!).

7. Trovare l’immagine tramite l’inversione circolare rispetto alla circonferenza goniometrica della retta r di equazione :

a) spiegare perché i punti (1, 0) e (0, 1) appartengono sia alla retta r che all’immagine della retta r;
b) disegnare r e la sua immagine in uno stesso grafico.

La soluzione degli esercizi precedenti porta ad enunciare il seguente:
Teorema (immagine di una retta tramite una inversione circolare)
Tramite l’inversione circolare rispetto ad una circonferenza di centro O:
a) una retta che non passa per O si trasforma in una circonferenza passante per O (privata del punto O);
b) una retta per O, ma privata di tale punto, si trasforma in se stessa.

Nello stesso modo si può arrivare ad enunciare e poi a dimostrare il seguente teorema:
Teorema (immagine di una circonferenza tramite un’inversione circolare)
Tramite l’inversione circolare rispetto ad una circonferenza di centro O:
c) una circonferenza che non passa per O si trasforma in una circonferenza che non passa per O;
d) una circonferenza per O, ma privata di tale punto, si trasforma in una retta che non passa per O.

Effetto dell’inversione circolare sugli angoli
La seguente proposizione descrive l’effetto dell’inversione circolare sugli angoli.
L’inversione circolare conserva gli angoli tra curve, ma scambia il loro orientamento.
Quindi l’inversione circolare è una trasformazione conforme (cioè mantiene gli angoli). Nella seguente figura sono segnate due rette perpendicolari tra loro e le loro trasformate (sono due circonferenze passanti per il punto O). Le due circonferenze si incontrano ortogonalmente in due punti (O ed un altro punto V’, che è l’immagine del punto V).

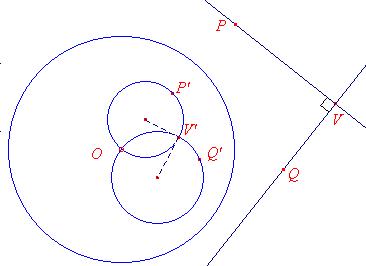
Effetto dell’inversione circolare su un angolo retto

Un invariante dell’inversione circolare: il birapporto
Dati quattro A, B, C, D, appartenenti ad una data retta orientata r, si chiama birapporto dei quattro punti, e viene indicato con il simbolo (ABCD), il seguente numero reale:

.

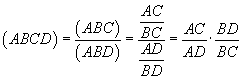dove AC, AD, BC, BD sono misure di segmenti orientati.

Occorre ricordare che

si chiama rapporto semplice dei tre punti allineati A, B, C.
Il birapporto possiede alcune proprietà che si possono studiare in modo dinamico e interattivo con l'aiuto di Cabri-géomètre:
- (ABCD) = 0 quando C coincide con A, oppure D coincide con B;
- (ABCD) = 1 quando C coincide con D, o A coincide con B;
- quando C tende a B, o A tende a D.
In tutti gli altri casi (ABCD) è un numero reale diverso da 0 e da 1. Tenendo fissi i punti A, B, C e facendo variare il punto D sulla retta, il birapporto è una funzione dell’ascissa x del punto D, che è un’iperbole equilatera.
Si ha infatti

.

Il birapporto (ABCD)>0 se i punti C e D sono entrambi interni o entrambi esterni al segmento AB, mentre è negativo in caso contrario.

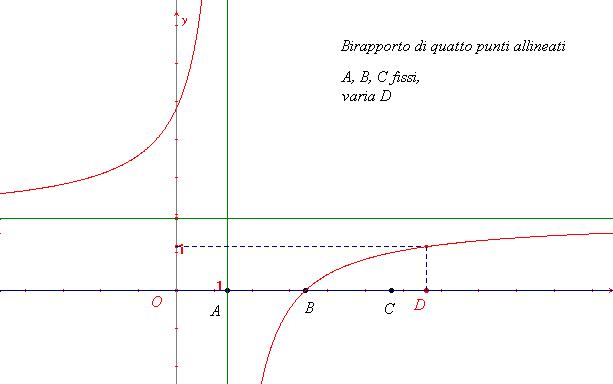
Studio del birapporto (ABCD) tra quattro punti di una retta orientata, al variare del punto D.

Il birapporto tra quattro punti A, B, C, D può essere definito anche se i punti appartengono ad una stessa circonferenza. Per fare questo occorre premettere la definizione di birapporto tra quattro rette di un fascio.
Si considerano le rette a, b, c, d, appartenenti al fascio di centro O. Si considera inoltre una retta r che non passi per O. La retta r incontra le rette a, b, c, d, rispettivamente nei punti A, B, C, D.
Si definisce birapporto tra le quattro rette a, b, c, d, appartenenti allo stesso fascio, il seguente numero reale:

.

La definizione di birapporto tra quattro rette viene ricondotta dunque alla definizione di birapporto tra quattro punti su una retta orientata.

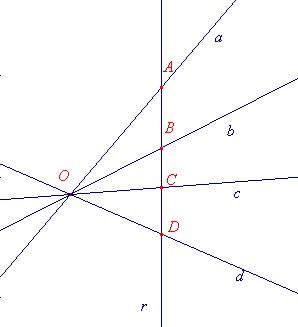
Birapporto tra quattro rette di un fascio

Si può dare la definizione di birapporto tra quattro punti di una circonferenza orientata. Dati quattro punti A, B, C, D su una circonferenza, si considera un punto S della circonferenza e si disegnano le rette SA, SB, SC e SD, chiamate rispettivamente a, b, c, d.
Intersecando le rette a, b, c, d con una retta r si ottengono i punti A’, B’, C’, D’. Si può dare ora la seguente definizione:

.

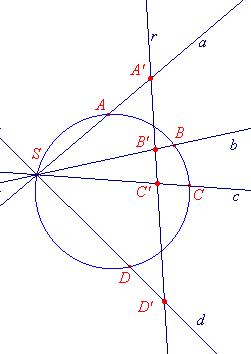
Birapporto tra quattro punti di una circonferenza

Fatta questa premessa, si può dimostrare la seguente importante proprietà:
Proprietà. Il birapporto tra quattro punti (appartenenti ad una retta orientata o ad una circonferenza orientata) è invariante rispetto all’inversione circolare.
Pertanto, se A, B, C, D sono quattro punti allineati e A’, B’, C’, D’ sono rispettivamente gli "inversi" rispetto ad una circonferenza w, allora il birapporto non cambia, ovvero:

(ABCD) = (A’B’C’D’).

Elementi uniti dell’inversione circolare e circonferenze ortogonali
Tutti i punti della circonferenza di inversione sono uniti. Sono inoltre unite (non di punti uniti) le rette passanti per O (ma private del punto O). I punti interni alla circonferenza di inversione si trasformano in punti esterni e viceversa. Sono invece punti uniti i punti di intersezione della retta con il cerchio di inversione.
Sono inoltre unite le circonferenze ortogonali alla circonferenza di inversione. Se una circonferenza passa per il punto P ed il suo inverso P’, allora è unita rispetto all’inversione circolare. Infatti, data la circonferenza , la “potenza” del punto O rispetto a rimane costante. Inoltre è ortogonale alla circonferenza . Ricordiamo che dato un punto O ed una circonferenza , si chiama potenza del punto O rispetto alla circonferenza , il seguente numero reale:

dove OP è una retta secante, oppure tangente, alla circonferenza. Per il teorema della secante e della tangente, si ha anche:

.

La definizione data di potenza di un punto O può essere generalizzata anche a punti interni alla circonferenza , ma in questo caso occorre usare un prodotto di misure di segmenti orientati e la “potenza” di un punto può anche essere negativa:

.

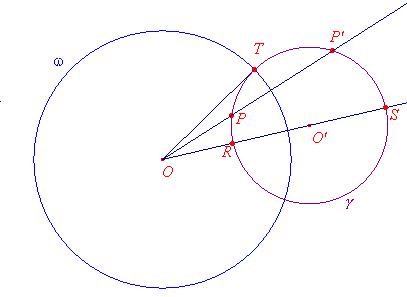
Circonferenze ortogonali e loro proprietà.

Ricordiamo che due circonferenze si dicono ortogonali se nei loro punti di intersezione le rette tangenti alle circonferenze sono perpendicolari.
Proprietà 1. Due circonferenze sono ortogonali se e solo se il quadrato della distanza tra i loro centri è uguale alla somma dei quadrati dei raggi delle due circonferenze.
Proprietà 2. Se due circonferenze sono ortogonali, il centro di ciascuna di esse è esterno all’altra circonferenza.
Proprietà 3. I punti d’intersezione di due circonferenze ortogonali si possono ottenere intersecandoli con la circonferenza che ha per diametro il segmento che unisce i loro centri.

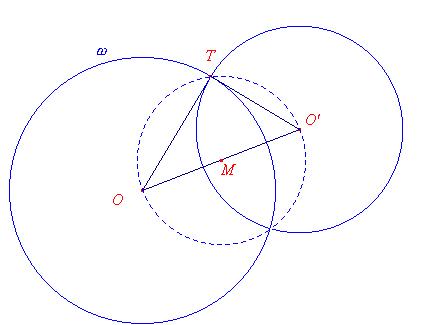
Circonferenze ortogonali.

Si ha inoltre la seguente proposizione:
Proprietà 4. Date due circonferenze ortogonali di centri O e O’ e raggi r ed r’, una retta passante per O e secante l’altra circonferenza, la interseca in due punti P e P’ tali che

.

Viceversa, se una retta passante per il centro di una circonferenza qualsiasi interseca un’altra circonferenza in due punti che soddisfano la relazione , allora le due circonferenze sono ortogonali.
La prima parte della proprietà 4 non è altro che l’enunciato del “teorema della secante e della tangente”. Si ha quindi:

.

Per dimostrare la seconda parte, si procede dall’ipotesi e si applica il teorema delle secanti:

.

Da quest’ultima relazione segue che

e quindi l’ortogonalità delle due circonferenze per quanto enunciato nella proprietà 1 (teorema di Pitagora).

Si ha come conseguenza la seguente proposizione:
Proposizione. Data una circonferenza w e, internamente ad essa, due punti A, B, non allineati con il centro O della circonferenza, esiste una ed una sola circonferenza passante per i due punti dati e ortogonale alla circonferenza data.

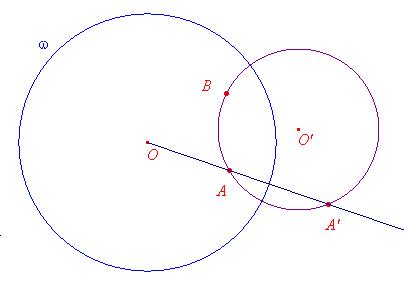
Circonfererenza per A e B ortogonale a

Siano A e B i punti interni al cerchio di inversione, non allineati con O. Costruiamo l’inverso circolare di A e lo chiamiamo A’. La circonferenza passante per A, B e A’ è quella richiesta. Infatti tale circonferenza è ortogonale alla circonferenza di inversione ed è unica. Nel caso in cui A e B siano allineati con O, la retta AB contiene un diametro del cerchio di inversione; anche in questo caso la retta è ortogonale al cerchio di inversione.

La circonferenza di Apollonio come applicazione dell’inversione circolare

Abbiamo visto in precedenza come costruire, data una circonferenza ed un punto P, l’inverso P’ rispetto alla circonferenza data. Poniamoci ora il problema di costruire la circonferenza, conoscendo inizialmente i punti P e P’; è chiaro che non basterà conoscere i punti P e P’ per individuare la circonferenza di inversione. Due punti dati P e P’, infatti, si corrispondono tramite una inversione circolare secondo infinite circonferenze.
Fissati due punti A e B e un numero reale positivo , cerchiamo il luogo geometrico dei punti tali che

.

Tale circonferenza si chiama circonferenza di Apollonio ed ha il centro sulla retta AB; si verifica allora che A e B si corrispondono rispetto all’inversione circolare stabilita nel piano dalla circonferenza di Apollonio (che manda A in B e B in A).

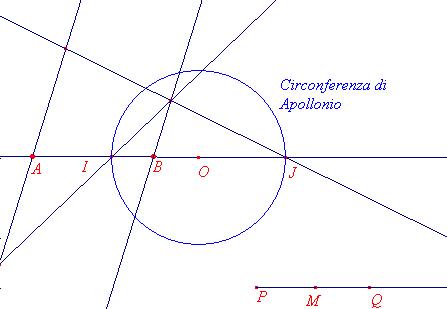
Costruzione della circonferenza di Apollonio.

Se k = 1, allora la circonferenza di Apollonio degenera in una retta, l’asse del segmento AB.