1.TEORIA ASSIOMATICO-DEDUTTIVA
In ogni scienza occorre precisare prima di tutto ciò che ne costituisce l’oggetto e poi dire quali sono i mezzi di ricerca.
In geometria gli enti di cui ci si occupa sono punti, rette, piani, segmenti, poligoni,... di cui si dà una definizione e dei quali si mettono in evidenza le proprietà secondo il procedimento logico della deduzione.
Ma definire un oggetto, un ente, significa porlo in relazione con altri enti che a loro volta per essere definiti dovranno essere messi in relazione con altri in un processo a ritroso che deve aver termine. Occorre dunque introdurre degli enti da considerare primitivi designati da nomi (“punto”, ”retta”, ”piano”,…) che ci richiamano alla mente immagini a noi familiari, nate da concetti ai quali conduce l’astrazione di modelli materiali (il segno lasciato dalla punta della matita, un granello di sabbia per il concetto di punto, un sottile filo teso per la retta o il segmento).
Una situazione del tutto analoga si ha per quanto riguarda il procedimento logico-deduttivo caratteristico delle dimostrazioni matematiche.
Dimostrare una proposizione significa dedurla, per mezzo di regole d’inferenza, da altre che a loro volta saranno dedotte da altre e così via all’infinito. Dobbiamo pertanto stabilire delle proposizioni da porre come base della nostra costruzione logica, delle asserzioni la cui validità è riconosciuta o comunque accettata: i postulati. Postulare significa domandare, richiedere, e in realtà è come se il matematico chiedesse ai suoi lettori di accettare, di accogliere, quanto in quelle proposizioni è affermato, in cambio egli mostrerà quali conseguenze se ne possono trarre, e quale imponente edificio di costruzione logica è possibile innalzare con quelle fondamenta.
Quale relazione esiste tra i concetti primitivi e i postulati di una teoria assiomatico-deduttiva?
I postulati servono a chiarire le proprietà dei concetti primitivi attraverso l’esplicitazione delle relazioni che intercorrono tra essi. E ne danno perciò una definizione implicita. Noi potremmo dimenticare il significato delle parole punto, retta, piano, ignorare ogni immagine da esse richiamato e riferirci solo al fatto che questi enti obbediscono alle proprietà espresse dai postulati.
I postulati costituiscono una convenzione ma per essere accettati devono soddisfare le seguenti condizioni:
compatibilità o coerenza: non possono contenere due affermazioni opposte A e ~A;
indipendenza: nessuno deve contenere un’affermazione che sia conseguenza dei rimanenti, altrimenti, se ciò accadesse, tra i postulati si nasconderebbero dei teoremi;
completezza: gli assiomi devono essere sufficienti a ricavare tutte le proposizioni della teoria.
I teoremi sono proposizioni che derivano logicamente dai postulati, sono enunciati condizionali che possono essere espressi nella forma “Se…(ipotesi, premessa) allora…(tesi, conclusione)”. Un teorema il cui enunciato non è in forma condizionale può essere sempre tradotto in tale forma che meglio evidenzia le ipotesi (proposizioni accettate come vere) e la tesi (proposizione da dimostrare). Ad esempio il teorema “In un triangolo i lati opposti ad angoli uguali sono uguali” può essere formulato così: “Se in un triangolo due angoli sono uguali, allora i lati opposti a tali angoli sono uguali”.
Nella dimostrazione di un teorema si accettano come veri l'ipotesi, i postulati e tutti i teoremi dimostrati.
La dimostrazione è costituita da una serie di enunciati, ciascuno con una sua giustificazione, che termina con la conclusione desiderata. Le giustificazioni sono solo dei seguenti sette tipi:
1. Per ipotesi (l’ipotesi del teorema che si accetta come vera);
2. Per l’ipotesi Reductio ad absurdum (RAA dimostrazione per assurdo);
3. Per un postulato;
4. Per un teorema precedentemente dimostrato
5. Per la definizione di un termine (mai di un termine primitivo);
6. Per un passo precedente della dimostrazione;
7. Per una regola di logica.
2. LA COMPATIBILITÀ DEI POSTULATI
Il problema della compatibilità dei postulati si mostra piuttosto complesso. Indichiamo con a l'insieme di postulati posti alla base della nostra geometria, e con S(a) la totalità delle proposizioni che si possono dedurre da essi, cioè la teoria assiomatico-deduttiva costruita sopra a
Supponiamo di aver dimostrato la seguente proposizione:
(1) I postulati a sono tra loro compatibili.
Possono presentarsi due casi:
a) La proposizione (1) appartiene al sistema S(a);
b) La proposizione (1) è fuori da S(a).
Nell'ipotesi a) la (1) è inattendibile, infatti, se i postulati a sono compatibili la (1) ne dà conferma, se non lo sono la (1) prova che esiste una contraddizione in S(a) e quindi prova la non compatibilità di a.
Pertanto la (1) ha valore solo nel caso b).
Ne segue che:
Non è possibile dimostrare la validità dei postulati a che stanno alla base di una teoria assiomatico-deduttiva S(a) senza uscire da questa
Quindi per accertarsi della compatibilità o coerenza dei postulati a della teoria S(a) occorre interpretare a facendo riferimento ad un'altra teoria assiomatico-deduttiva S(b) e dimostrare la compatibilità delle proposizioni a in S(b); ma affinché si possa riconoscere la non contraddizione degli enunciati a occorre che anche i postulati b, che sono alla base della teoria S(b) siano compatibili, e per giungere a ciò bisogna ripetere per S(b) quanto si è detto per S(a), e pertanto occorre far ricorso ad un nuovo sistema ipotetico-deduttivo S(g), dal quale, a sua volta, dovremo passare ad un quarto, e così via.
Si rinnova una situazione che abbiamo incontrato quando abbiamo affrontato il problema della definizione dei termini e della dimostrazione dei teoremi, un processo a ritroso che deve avere termine in un punto di partenza.
Bisogna cioè ricondurci ad un sistema ipotetico-deduttivo S*, da considerare come primitivo, la cui verità viene senz'altro accettata.
Di solito viene scelto come S* il sistema dei numeri naturali, i cui postulati riteniamo compatibili. Ma la coerenza degli assiomi su cui si fonda la teoria dei numeri naturali non può essere dimostrata con strumenti matematici.
L'impossibilità per la matematica di dimostrare la sua coerenza attraverso strumenti matematici, è stato un risultato a cui è pervenuto, nel 1931, il logico matematico, Kurt Gödel (1906-1978):
È impossibile stabilire la coerenza logica di un qualunque sistema deduttivo complesso, a meno di usare dei princìpi di ragionamento la cui coerenza interna è problematica quanto quella del sistema stesso.
3. EUCLIDE
Il primo che ha tentato una sistemazione rigorosa, una assiomatizzazione, delle conoscenze di geometria del piano e dello spazio, è stato Euclide (300 a.C.) negli Elementi, il libro più tradotto nel mondo dopo la Bibbia.
Egli definisce i termini, e pone alla base della sua teoria 8 assiomi (o nozioni comuni) e 5 postulati.
Per Euclide gli assiomi sono «verità ammesse da tutti, alle quali l'uomo inevitabilmente ricorre tanto in ciascuna scienza, quanto in qualsiasi ragionamento quotidiano»; mentre i postulati sono «le richieste, che il lettore deve accettare, accingendosi allo studio di una disciplina (in questo caso la geometria), affinché i ragionamenti successivi non suscitino obiezioni da parte sua»[1].
ASSIOMI (o nozioni comuni)
1) Se due cose sono uguali a una stessa cosa, sono uguali tra loro.
2) Se a due cose uguali si aggiungono cose uguali, le somme sono uguali.
3) Se da cose uguali si sottraggono cose uguali, le differenze sono uguali.
4) Cose che si possono sovrapporre l’una sull’altra sono uguali tra loro.
5) Il tutto è maggiore della parte.
6) Eguaglianze e diseguaglianze fra grandezza geometriche del medesimo tipo obbediscono alle stesse leggi delle eguaglianze e diseguaglianze fra numeri interi positivi.
Gli assiomi (tranne il 4) si possono esprimere in forma algebrica, indicando con a, b, c, d grandezze omogenee, che in geometria piana sono di tre tipi: lunghezze di linee finite, ampiezze di angoli e aree.
1) (a = b Ù c = b) Þ a = c.
2) (a = b Ù c = d) Þ a + c = b + d.
3) (a = b Ù c = d) Þ a − c = b − d.
4) a + b > a.
POSTULATI
1) Due punti sono congiunti da una sola retta.
2) Una retta può essere prolungata indefinitamente da ambo le parti.
3) Con un dato centro e un dato raggio si può tracciare una circonferenza.
4) Tutti gli angoli retti sono uguali tra loro.
IL QUINTO POSTULATO DI EUCLIDE

Se due rette sono intersecate da una trasversale in modo tale che da una parte di questa la somma degli angoli è minore di un angolo piatto, le due rette allora si incontrano da quella parte.
4. HILBERT
Il matematico tedesco David Hilbert (1862-1943) nel saggio Grundlagen der Geometrie (I fondamenti della geometria), pubblicato nel 1899, intraprese una revisione della geometria euclidea volta a eliminare dalla geometria l'intuizione e a rifondarla come sistema ipotetico-deduttivo.
Vengono introdotti tre insiemi di enti primitivi : si chiamano punti gli oggetti del primo insieme, rette quelli del secondo, piani quelli del terzo. Ma dobbiamo dimenticare il significato di questi termini e l'immagine che tali parole evocano (dobbiamo, dice scherzando H., poterci riferire in ogni momento a tavoli, sedie e boccali di birra al posto di punti, rette, piani), tali enti sono definiti implicitamente dai postulati, che H. divide in 5 gruppi: assiomi di appartenenza, di ordinamento, di congruenza, di parallelismo, e di continuità. Ne citiamo solo alcuni.
Assiomi di appartenenza:
1. Per ogni coppia di punti distinti esiste una e una sola retta a cui appartengono entrambi (in realtà H. formula l'assioma così: per ogni coppia di elementi A e B del primo insieme, esiste uno e un solo elemento r del secondo insieme tale che A e B siano in relazione con r).
2. Data una retta esiste almeno un punto che non le appartiene.
3. Ad ogni retta appartengono almeno tre punti.
Da questi assiomi segue che due rette o hanno un solo punto in comune o nessuno. È possibile dare la definizione di parallelismo tra rette in un piano: due rette sono parallele se non hanno alcun punto in comune oppure se coincidono in questo modo il parallelismo è una relazione di equivalenza nell'insieme delle rette del piano: la direzione è la classe di equivalenza individuata da una retta e da tutte quelle ad essa parallele.
Assioma del parallelismo
Data una retta r e un punto A che non appartiene a r, esiste al più una retta passante per A e parallela alla retta r.
5. TEOREMI DIMOSTRATI SENZA IL QUINTO POSTULATO
Il primo libro degli Elementi contiene 48 proposizioni o teoremi, i primi 28 dei quali, assieme al teorema 31, vengono dimostrati senza far uso del quinto postulato. Ne citiamo alcuni.
Teorema 3
Date due rette disuguali è possibile staccare sulla maggiore una retta uguale alla minore (ricordiamo che Euclide intende per retta un segmento).
Teorema 4
Se due triangoli hanno rispettivamente uguali due lati e l'angolo compreso, allora sono congruenti.(Quello che in termini moderni viene indicato come primo criterio di congruenza dei triangoli)
Teorema 5
Nei triangoli isosceli gli angoli alla base sono congruenti.
Teorema 8
Se due triangoli hanno rispettivamente uguali i tre lati, allora sono congruenti. (terzo criterio)
Teorema 10
È possibile dividere a metà una retta finita assegnata.
Teorema 13

Se una retta viene innalzata su un'altra retta, verrà a formare con essa o due angoli retti o angoli la cui somma è uguale a due retti.
Teorema 15
Se due rette si intersecano formano angoli opposti al vertice tra loro uguali.
Teorema 16
In qualunque triangolo, se si prolunga uno dei lati, l'angolo esterno è maggiore di ciascuno dei due angoli interni e opposti (cioè non adiacenti ad esso).
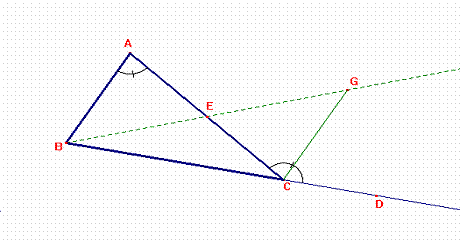
Ipotesi: Sia ABC il triangolo e prolunghiamo il lato BC fino a D: in questo caso l'angolo esterno è ÐACD e gli "angoli interni e opposti" sono ÐCAB e ÐABC;
Tesi: (a) ÐACD > ÐCAB (b) ÐACD > ÐCBA.
Dimostrazione:
1. Sia E il punto medio del lato AC ( teorema 10);
2. Tracciamo BE ( postulato 1);
3. Prolunghiamo BE dalla parte di E ( postulato 2);
4. Su EF prendiamo EG = BE ( teorema 3);
5. Tracciamo GC (postulato 1);
6. ÐAEB = ÐGEC ( teorema 15);
7. I triangoli AEB e GEC sono congruenti (@) (1.4.6 teorema 4);
8. ÐBAC = ÐACG (definizione di "congruente");
9. ÐACD > ÐACG ( assioma 5);
10. ÐACD > ÐBAC ( 8.9 Assioma 6);
Abbiamo così dimostrato(a);in maniera analoga si dimostra (b).
Teorema 17
In ogni triangolo la somma di due angoli, comunque presi, è minore di due retti.
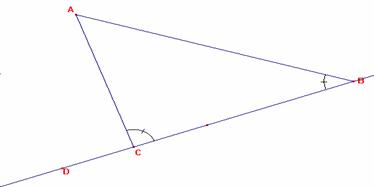
Ipotesi: ABC è un triangolo qualsiasi.
Tesi: ÐABC + ÐACB < due retti.
Dimostrazione:
1. Prolunghiamo BC fino a D ( postulato 2)
2. ÐACD > ÐABC ( teorema 16 )
3. ÐACB + ÐACD > ÐACB + ÐABC ( assioma o nozione comune 2)
4. ÐACB + ÐABC < 2 retti ( teorema 13)
Il teorema è così dimostrato.
Se si pensa ad una retta intersecata da altre due, questo teorema risulta l'inverso del quinto postulato: quest'ultimo afferma che, se la somma dei due angoli coniugati interni è minore di due retti, le due rette si incontrano, formando quindi un triangolo, viceversa, per il teorema 17, se le due rette formano con la terza un triangolo, la somma dei due angoli è minore di due retti.
Teorema 28
Se, allorché due rette sono intersecate da una trasversale, sussiste tra gli angoli da esse formati una qualsiasi delle seguenti otto relazioni: angoli alterni interni uguali, alterni esterni uguali, angoli corrispondenti uguali e angoli interni dalla stessa parte (coniugati) la cui somma sia uguale a due retti, allora le due rette sono parallele.
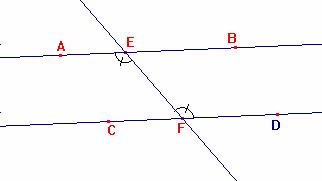
Ipotesi: Siano AB e CD due rette ed EF la retta che le interseca, rispettivamente in E e in F, in modo tale che ÐAEF = ÐEFD (alt.interni); Tesi: AB//CD.
Dimostrazione:
1. Supponiamo, per assurdo, che le due rette non siano parallele, cioè che, ad esempio, i prolungamenti di AB e CD dalla parte di B e D si incontrino in un punto G ( R.A.A.);
2. ÐAEF > ÐEFD ( teorema 16 applicato al triangolo EFG);
3. Contraddizione (2.ipotesi);
4. Pertanto le due rette non si incontrano ( Logica).
Lo stesso ragionamento si può fare per l'altro lato, pertanto il teorema è completamente dimostrato.
Teorema 31
Per un punto dato, non giacente sulla retta né sul suo prolungamento, è possibile tracciare una retta parallela alla retta data.
Questo teorema è l'ultimo del primo libro che si possa dimostrare senza far riferimento al quinto postulato; in esso Euclide, dopo aver parlato di rette parallele, verifica la loro esistenza.
6. TEOREMI DIMOSTRATI FACENDO USO DEL QUINTO POSTULATO
I rimanenti teoremi del libro I ( 29, 30, 32-48) dipendono dal quinto postulato.
Anche in questo caso ne citeremo solo alcuni.
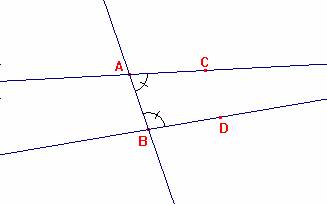
Teorema 29 (inverso del 28)
In un piano, una retta che intersechi due rette parallele forma con esse angoli alterni interni uguali fra loro, angoli alterni esterni e corrispondenti uguali fra loro, e angoli interni da una medesima parte la cui somma è due retti.

Ipotesi: AB//CD e sia EF la trasversale che le interseca rispettivamente in E e in F Tesi: ÐAEF = ÐEFD
Dimostrazione:
1. Supponiamo che ÐAEF ¹ ÐEFD e sia, ad es., ÐAEF > ÐEFD (R.A.A.);
2. ÐAEF + ÐBEF > ÐEFD + ÐBEF (1. Assioma 6);
3. ÐAEF + ÐBEF = due retti ( teorema 13);
4. ÐEFD + ÐBEF < due retti (2. 3. Assioma 6);
5. AB e CD si incontrano dalla parte di EF dove stanno B e D (4. Quinto postulato);
6. Contraddizione ( 2. 5.);
7. perciò ÐAEF = ÐEFD (1. 6. Logica).
Il teorema è dimostrato.
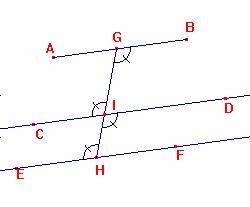
Teorema 30
Rette parallele ad una stessa retta sono parallele tra loro.
Ipotesi: AB//EF Ù CD//EF;
Tesi: AB// CD.
Nella dimostrazione vi sono da considerare due casi, a seconda che le rette sono dalla stessa parte o da parte opposta rispetto alla retta a cui risultano entrambe parallele.
Dimostrazione primo caso:
1. Siano AB e CD due rette parallele alla medesima retta EF e giacenti dalla stessa parte di EF ( ipotesi);
2. Scegliamo a caso un punto G sulla retta più lontana da EF, nel nostro disegno AB, e un punto H su EF e tracciamo GH ( postulato 1);
3. GH interseca CD in un punto I, ÐBGI = ÐEHI (1. Teor.29);
4. ÐDIH=ÐEHI (1. Teor.29);
5. ÐBGI=ÐDIH (3.4. assioma 1);
6. ÐCIG=ÐDIH (teorema 15);
7. ÐBGI=ÐCIG (5.6. assioma1);
8. AB è parallela a CD. (7. Teor.27/28).
Teorema 32
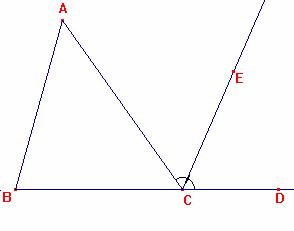
In ogni triangolo, se si prolunga uno dei lati: (a) l'angolo esterno è uguale alla somma dei due angoli interni opposti; (b) la somma dei tre angoli interni è uguale a due retti.
Ipotesi: ABC è un triangolo qualsiasi, prolunghiamo BC fino a D e consideriamo l'angolo esterno ÐACD;
Tesi:(a)ÐACD=ÐBAC + ÐCBA (b)ÐACB + ÐBAC + ÐABC = due retti.
Dimostrazione:
1. Per C tracciamo CE parallelamente ad AB ( teor.31);
2. ÐBAC = ÐACE (teor.29 AC interseca AB//CE);
3. ÐABC = ÐECD teor.29 BD interseca AB//CE);
4. ÐBAC + ÐABC = ÐACE + ÐECD (2. 3. Assioma 2);
5. ÐACD = ÐACE + ÐECD ( assioma 1);
6. ÐACD = ÐBAC + ÐABC (4. 5. Assioma 1);
Abbiamo così dimostrato la parte (a) della tesi.
7. ÐACB + ÐACD = ÐACB + (ÐBAC + ÐABC) (6. Assioma 2);
8. ÐACB + ÐACD = due retti ( teorema 13);
9. Perciò ÐACB + ÐBAC + ÐABC = due retti. (7. 8. Ass.1).
Così il teorema è completamente dimostrato.
La dipendenza dal quinto postulato è implicita nei passi 2. e 3. in quanto in essi si fa uso del teorema 29 che è stato dimostrato per mezzo del quinto postulato.
Teorema 34
I parallelogrammi hanno lati e angoli opposti uguali fra loro e sono divisi dalla diagonale in due parti uguali.
In questo teorema Euclide parla dei parallelogrammi senza averli mai definiti prima, ma il significato del termine appare chiaro dall'uso che ne fa in seguito.
Teorema 46
Data una linea retta è possibile costruire su di essa un quadrato.
Con questo teorema è assicurata l'esistenza dei quadrati e quindi dei rettangoli.
Teorema 47 (Teorema di Pitagora)
Nei triangoli rettangoli il quadrato costruito sul lato opposto all'angolo retto è uguale alla somma dei quadrati costruiti sui lati che comprendono l'angolo retto (cioè sui cateti).