Cenni all'universo di Minkowski...
La
teoria del moto può riguardare anche una geometria nello spazio a quattro
dimensioni x, y, z, t (l'universo di Minkowski: 1907, fu tra
l’altro professore di matematica di Einstein al Politecnico di Zurigo).
I punti dello spazio-tempo di Minkowski sono
“eventi”, cioè vanno caratterizzati non solo da una serie di coordinate
spaziali, ma anche da una coordinata temporale che specifica l'attimo in cui si
svolge l'evento. Per intenderci, un aeroplano in volo non è un evento, bensì
una serie continua di eventi che si snoda nello spazio-tempo di Minkowski. Ma quale
significato assumono allora i sistemi inerziali e le trasformazioni di Galileo
in tale geometria quadridimensionale. Non è affatto difficile scoprirlo, in
quanto le coordinate y e z non entrato affatto nella trasformazione; è
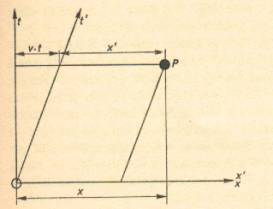
sufficiente quindi operare nel piano x,t. Supponiamo che il nostro sistema
inerziale S sia rappresentato da un sistema di coordinate rettangolari x,t (vedi
fig.), e che un secondo sistema inerziale, S', corrisponda al sistema di
coordinate x',y'.
Ci
si pone il problema: quale posizione assume il secondo sistema rispetto al
primo, e che relazione intercorre fra i due? Anzitutto, la misura del tempo è
esattamente la stessa in entrambi i sistemi; è data cioè dal tempo assoluto
t=t'. Quindi i due sistemi hanno l’origine in comune. Di conseguenza il
sistema S' potrà essere soltanto un sistema di coordinate oblique.
Secondo il principio galileiano concludiamo dicendo che nel piano x,t la scelta della direzione dell’asse t è completamente arbitraria; in ogni sistema di coordinate x,t avente lo stesso asse x, sono valide le leggi fondamentali della dinamica.
LA FOTO E' RICAVATA DAL LIBRO DI MAX BORN, LA SINTESI EINSTEINIANA.