Le trasformazioni di Galileo...

Per quanto le leggi della meccanica siano le stesse in tutti i sistemi inerziali, da ciò non segue naturalmente che le coordinate e le velocità dei corpi rispetto a due sistemi inerziali siano uguali. Si pone quindi il problema di trovare la posizione e la velocità di un corpo in un dato sistema inerziale S', una volta che queste siano note per un altro sistema inerziale S. Si tratta di passare insomma da un certo sistema di coordinate, a un altro sistema in moto rispetto al primo. Dobbiamo però specificare esattamente di quanto il sistema si è spostato o è ruotato, in modo da determinare adesso, nel nuovo sistema S', le coordinate di un generico punto P, i cui valori erano x e y nel vecchio sistema S. Se indichiamo le nuove coordinate con x', y', otteniamo delle formule che ci permettono di calcolare x' e y' una volta note x e y (equazioni di trasformazione). Nella fig. si vede che la nuova coordinata x' del punto P sarà uguale alla corrispondente coordinata x, che esso aveva nel vecchio sistema di riferimento, diminuita dello spostamento d; mentre la coordinata y resta invariata; si ha cioè:

x'=x-d  y'=y.

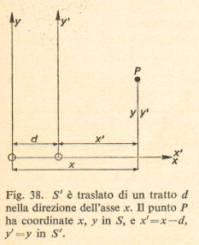
Dato che d=vt si otterranno le nuove equazioni di trasformazione:

x'=x-vt  y'=y  z'=z

Gli invarianti

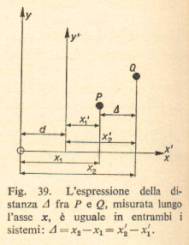
È importante osservare che si possono trovare delle quantità la cui espressione non cambia al variare del sistema di riferimento che si considera. Tali quantità sono dette invarianti. Se consideriamo, ad esempio, la fig. sotto che rappresenta una traslazione lungo l'asse x, si ha ovviamente che la differenza D fra le coordinate x di due punti P e Q non cambia.

LE FOTO SONO RICAVATE DAL LIBRO DI MAX BORN, LA SINTESI EINSTEINIANA.