
Karma Engine Parameters Compendium[2006.07.06] |
 |
|
The Karma engine and its parameters are not an easy subject. That's why I've written the following compendium merging the relevant information contained in these 3 sources:
I corrected some error, added some comment and further info and organized the contents in a hopefully synthetical and clear form.
There are few, important things that you should know before building any Karma object:
It is convenient in simulation to represent a virtual world object as three separate parts, namely the dynamic body, collision frame and rendered object. These can be manipulated individually, but are more likely to be linked by using the same position and orientation information for each.
A physics simulation with collision detection can evolve without any graphical display. However it is often convenient for the user to render the scene to observe the behavior.
 |
Collision objects are much simpler then rendered objects as they are subject to complex computations, that's why the best geometries to use for this purpose are: spheres, cylinders and boxes. The idea is to approximate the rendered mesh with one or more of these primitives. Karma allows to use even convex (!) triangle meshes for collisions, but they are computationally much more expensive and should be used only if really needed. If more then one primitive is needed to approximate an object, a small gap should be left between them.
 |
 |
|
Convex and non convex mesh |
AIBO uses all the collision primitives. A single convex triangle mesh is used to approximate the head because a box would be too rough. |
Karma uses a Lagrange multiplier method to model jointed systems and contacts. In such a model, the effect of constraints is modeled by forces that act to maintain the constraint. In order to calculate these forces, a type of matrix problem called a linear complementarity problem (LCP) is solved. Karma’s LCP solver is called Kea. Kea calculates forces which when applied, satisfy the constraints at the end of the time-step.
The Kea integrator provides two user parameters, Epsilon and Gamma. These can be adjusted to affect how the integrator steps the system from one state to the next.
Epsilon [default: 0.001]. At every time-step, Kea must solve a matrix equation of the form ( A + ε I )X = B. Epsilon is added to the diagonal of the constraint matrix to improve Kea's ability to solve this problem. The following symptom suggest that the solver is having difficulty determining the forces:
This problem can be fixed by increasing Epsilon. The only disadvantage of increasing Epsilon is that it makes the joints and constraints a little bit springy instead of being solid. This is usually not a problem. Values of Epsilon (such as the default 0.01) can be effective, and a value of Epsilon near 1 is large and will almost certainly give visible springiness in the constraints - an indication that Epsilon may be too large.
Gamma. Every time-step, after Kea has determined the forces on the rigid bodies, the positions and velocities of those
bodies are updated. The way that this is done can cause the joints and other constraints to pull away from
each other, so that objects will not be in their correctly constrained configurations in the new state.
Kea minimizes this problem through a relaxation process, which is controlled by Gamma, a positive number that is
a relaxation rate.
When positions are updated, projection moves the rigid bodies Gamma of the way back to their correctly
constrained configurations. Gamma applies to contacts as well - objects may penetrate a bit before a contact is
generated, and the bodies then have to be projected apart again.
As Gamma*h should be constant, UT doesn't allow to modify directly Gamma value but rather Gamma*h where h is fixed to 1 second. That's why that parameter is called GammaPerSec [default: 6.0] in UT.
PenetrationOffset [default: 0.01] (karma units). This appears to be added to the actual penetration when the object is consider "at rest." IE, when it's not moving, it's assumed to be penetrating the world by this much, meaning it has to be "dislodged" by some amount of force in order to move it. This helps to keep actors at rest resting, instead of the simulation being restarted from the slightest thing. Obviously, larger values make actors more difficult to "dislodge" from rest. Negative values might not be allowed, but if they are, they would probably make things appear to vibrate when "at rest."
PenetrationScale [default: 1.0]. Penetration is multiplied by this amount. Since interpenetration is caused by collision, this causes objects to appear to have impacted each other much harder (or softer, if the value is lower) than they really did.
ContactSoftness [default: 0.01] (karma units). When two objects collide, there will be some initial inter-penetration. The amount of penetration depends on how fast the two objects were going before they collided. After collision, Kea's projection feature will push the objects apart to reduce the penetration to zero. However, sometimes Kea will push the objects too far, and the contact will be broken. This can be a problem, for example, when objects are resting on the ground. When the contact is broken, the object will “fall” a short distance into the ground, the contact will be re-made and the object will be pushed out again. This process can result in resting objects that jitter or twitch from time to time. One solution is to set the softness option on the contact. This will cause two objects that are being forced together to naturally inter-penetrate slightly, preventing contact breaking.
MaxPenetration [default: 0.13] (karma units). The maximum amount of penetration allowed. Since penetration is generally the result of collision, penetration is assumed to be the result of collision if it is below this amount, and the objects will "bounce" off each other with stiffness and such determined by their KarmaParams. Above this amount, the two objects are assumed to in fact not be colliding, but instead one is impaled on the other and should not bounce off but instead remain within the other actor. The penetration is merely assumed to be not the result of a collision, so the actors won't "push off" each other.
MaxTimeStep [default: 0.04].
This is the maximum "tick" allowed to the Karma system. So, if it was 100 ms, and you were getting 1 fps, the simulation would update 10 times per frame with a "deltatime" of 100ms each time. This does not actually affect the Tick in script, but the analogy was provided for illustrative purposes. If your framerate is sufficiently high, then the Karma simulation will just update once every frame. The default is 0.04, which is 40ms, so if you are getting more than 25 fps, Karma updates once per frame. Lower values will give a more precise simulation, but are likely directly proportional to the performance of the Karma system. Note that there appears to be a maximum number of updates per tick, so if you set this too low (too precise of simulation) the simulation will be slowed down to fit within the maximum updates per tick.
These values apply to any Karma simulated actor using KarmaParams or one of it's subclasses as it's KarmaParams.
KMass [default: 1.0]. This is the Actor (object) mass.
KLinearDamping [default: 0.2]. This is the amount of force applied to reduce linear motion of the Actor causing translational drag. The greater the value the more it will resist movement in a linear direction. Note that this is in addition to any friction from other surfaces it touches.
KAngularDamping [default: 0.2]. This is the amount of force applied to reduce angular motion of the Actor to create rotational drag. The greater the value, the more it will resist rotation. Note that this is not the same as inertial resistance from attempting to rotate an unbalanced object.
KFriction [default: 0.0]. This is the amount of friction this object will experience and exert on other objects it comes into physical contact with. 0 is frictionless, while a value of 1 will exert a lot of friction on objects it contacts. With a value greater than 1 the object may never achieve a state of rest or always remain at rest.
KActorGravScale [default: 1.0]. This is how much gravity affects this object. It is used primarily to create special effects and also to give a different impression to an object. For instance, a large, heavy object may have this set higher to make it "feel" heavier, without it's mass actually being higher. This can make it easier to move while being equally difficult to take off the ground. 0 means gravity has no effect on this actor. Negative values are possible and will cause the object to gravitate in the opposite direction by the factor specified. This multiplier will be overridden by a PhysicsVolume though.
KMaxSpeed [default: 2500.0] (unreal units). Maximum allowed speed.
KMaxAngularSpeed [default: 10.0] (radians/sec). Maximum allowed angular velocity.
KBuoyancy [default: 0.0]. This will allow the Karma Actor to be able to float within a WaterVolume. If it is 0, the object will fall through water as if it were falling through empty air. A value of 1 will cause the Actor to free float in the direction it was last moving in until it comes to rest. In order for the Actor to float upwards, it must have a setting greater than 1 even if only slightly.
KRestitution [default: 0.0]. This determines the ‘bouncyness' of the Karma Actor, where 0 = no bounce and 1 = incoming velocity is equal to outgoing velocity.
KImpactThreshold [default: 1000000.0] (unreal units). If the actor is impacted by another Karma object at a velocity greater than this setting, an event will be triggered in the Unrealscript for that object. Note that the velocity is in Karma units, and, like mass, is not the same scale as the regular physics engine.The event that is triggered is as follows:
event KImpact (actor other , vector pos , vector impactVel , vector impactNorm)
Other is the object that impacted this actor. Pos is the position of the impact. ImpactVel is the velocity of the impact, and ImpactNorm is the normal vector of the impact.
KStartEnabled [default: false]. If this is set to true, the object will begin simulating as soon as it is created. If it is set to false, the object will lie dormant and will not simulate until it is interacted with by another Karma actor through collision, or if it is shot by a weapon.
KStartLinVel [default: (0,0,0)] (unreal units). A vector describing the initial velocity of this actor when it is spawned/the level is loaded.
KStartAngVel [default: (0,0,0)] (unreal angles). A vector describing the initial angular velocity, or rotation rate, of this actor when it is spawned/the level is loaded.
bKNonSphericalInertia [default: false]. Describes how mass distribution should be calculated. If it is false the object is assumed to have it's mass distributed spherically. If it is set to true, the inertia will be calculated based on the collision hulls of the object. The object is assumed to be uniformly dense for this purpose. Center of mass is also calculated automatically based on this information. If you want to override either of these values you must use KarmaParamsRBFull . This value defaults to false, so spherical inertia is used by default.
KStayUpright [default: false]. If this is set to true, the actor will remain upright. This means that it will not be permitted to roll or pitch, it may only yaw. If KAllowRotate is also false, it may not yaw either.
KAllowRotate [default: false]. If KStayUpright is set to true, and this value is set to true, the actor may pivot on it's Z axis. (yaw) If KStayUpright is set to true and this is set to false, the object may not rotate at all. If KStayUpright is set to false this setting has no effect.
These values apply only to Karma Rigid Bodies. They have no effect on Karma Ragdolls.
bHighDetailOnly [default: true]. If this variable is set to true, this actor will only be simulated if the physics detail is set to PDL_High. If this variable is set to false, Karma physics will be used as long as the physics is PHYS_Karma. If this variable is set to true and the physics detail is not PDL_High, this object will use normal physics only.
bClientOnly [default: true]. If this variable is set to true, the actor will simulate client-side and will not have it's simulation information replicated constantly. For obvious reasons, this should only be used for benign objects that will not collide with anything, or, like swinging meat on the roof, will not move enough to make an appreciable difference in collision. It can also be used for objects which will not be collided with, such a ceiling fan that is high up out of reach.
bKDoubleTickRate [default: false]. If this is set to true, the object will be simulated twice as frequently as objects who have this set to false. Note that on rare occasions, objects with bKDoubleTickRate set to true may not collide with objects that have it set to false.
bDestroyOnSimError [default: true]. If this is set to true, the actor will be destroyed if a simulation error occurs. This generally only happens if for whatever reason a Karma object is spawned deep within BSP geometry, though theoretically it can occur under different circumstances. This is usually true on servers and false on clients. If a client has a simerror and the server does not, the server will fix the Karma simulated object when it is next replicated. If the server suffers a simerror it will replicate the destruction of the object even if the clients have bDestroyOnSimError set to false.
This is a more advanced, but otherwise functionally identical version of KarmaParams. It allows control over the center of mass and its inertial properties. It adds the following variables:
KInertiaTensor [default: Ixx = Iyy = Izz = 0.4]. The inertial tensor of a body, I, is represented by a 3 by 3 matrix, where the offdiagonal components of the matrix are usually zero, and the diagonal components Ixx, Iyy and Izz give the moments about the principle x, y and z axes. Ixx, Iyy and Izz determine how hard it is to rotate an object about a principle axis. Inertia tensor assumes a mass of 1. That means that its values will be scaled by the actual object mass.
 |
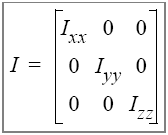 |
KCOMOffset [default: (0,0,0)] (karma units). The center of mass offset. This is a vector indicating the location of the center of mass of this actor in its local coordinate system.