Primo termine a secondo membro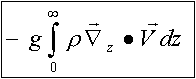
|
rappresenta l'influenza della divergenza orizzontale del vento al di
sopra del livello z.
|
 |
 |
la pressione resta costante
|
|
 |
 |
la pressione diminuisce poiché l'aria in prevalenza abbandona la
colonna atmosferica
|
|
 |
 |
la pressione aumenta poiché l'aria in prevalenza affluisce nella
colonna atmosferica
|
|
Secondo termine a secondo membro
|
è il contributo alla variazione della pressione dato dall'avvezione
di densità.
|
 |
=0: la pressione resta costante se non c'è avvezione di densità
né quindi di temperatura
|
 |
>0: la pressione aumenta se c'è avvezione di aria più densa
(più fredda)
|
 |
<0: la pressione diminuisce se c'è avvezione di aria meno
densa (più calda)
|
|
 [2]
[2]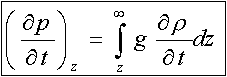

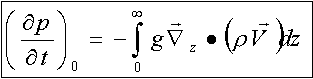

![]()