ANALISI TEORICA DEL FENOMENO

[Introduzione]

[Strumenti e materiali usati]
"Però ditemi: quando voi aveste una superficie piana, pulitissima  come uno specchio e di materia dura come l'acciaio, e che fusse non parallela all'orizonte, ma alquanto inclinata, e che sopra di essa  voi poneste una palla perfettamente sferica e di materia grave durissima, come, verbigrazia, di bronzo, lasciata in sua libertà che credete voi che ella facesse? Non credete voi  (sì come credo io) che ella stesse ferma?"    

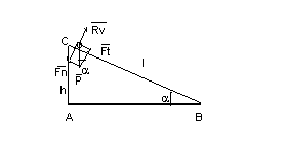
Analizziamo teoricamente  il fenomeno della caduta di una sferetta su un piano inclinato cercando di prevedere (sempre per via teorica) che cosa può succedere dal punto di vista cinematico e dinamico nel momento in cui  abbandoniamo il corpo in cima al piano inclinato senza attrito. Secondo Galileo : " un mobile grave descendente partirsi dalla quiete, cioè dalla privazione di ogni velocità, ed entrare nel moto, ed in quello andarsi velocitando secondo la proporzione che cresce 'l tempo dal primo instante del moto, ed havere in otto battute di polso acquistato otto gradi di velocità, della quale nella quarta battuta ne haveva guadagnati quattro, nella seconda due, nella prima uno, essendo il tempo subdivisibile in infinito".

Osserviamo la figura 1 :

In essa compaiono l'altezza h del piano inclinato, la sua lunghezza l e l'angolo d'inclinazione a . In relazione al corpo di massa m notiamo la presenza della forza pesoesercitata dalla Terra e delle due componenti di quest'ultima Fn ed Ft rispettivamente perpendicolare e parallela al piano inclinato. Delle due, la prima (Fn ) è equilibrata dalla reazione vincolare Rv prodotta dal piano inclinato sul corpo mentre la forza Ft non essendo equilibrata sarà la causa che metterà in movimento il corpo. Inoltre, dato che questa forza non ha ragione di cambiare durante il moto della pallina, per il 2° principio della dinamica essa sarà costante. Dunque, anche l'accelerazione sarà costante (a = F/m = cost) e il moto sarà moto rettilineo uniformemente accelerato.

Per calcolare questa accelerazione basta rilevare la similitudine tra i due triangoli rettangoli ABC e quello delle forze di lati P, Ft ed Fn .

Dunque Ft : P = h : l , da cui Ft  = (h/l)P. Anche qui, dato che h, l e P sono costanti se ne deduce che Ft è costante. L'accelerazione della pallina si ottiene molto semplicemente sostituendo ad Ft il prodotto ma. Pertanto ma =(h/l)mg . In realtà avremmo dovuto più correttamente scrivere:

dove con mi si indica la massa inerziale e con mg la massa gravitazionale della pallina. Com'è noto i due concetti sono profondamente diversi.  Nel caso in cui la massa inerziale mi della pallina è uguale alla massa gravitazionale ( mg) della medesima, si ha:

Poiché h è sempre minore di l ( la lunghezza di un cateto è sempre minore della lunghezza dell'ipotenusa) è anche a<g : il corpo scende sul piano inclinato con accelerazione inferiore a g, ma in ogni caso di moto rettilineo uniformemente accelerato, l'entità del quale dipende dal valore dell'angolo di inclinazione del piano inclinato.

Quanto precede costituisce l'aspetto predittivo della legge fondamentale della meccanica di Newton, in cui la forza è la causa del tipo di moto e l'accelerazione ne rappresenta l'effetto.

Teoricamente, dunque, si ottiene una affermazione decisamente forte ( l'accelerazione di un corpo in moto su un piano inclinato è costante e uguale a una frazione h/l dell'accelerazione di gravità), che è necessario controllare empiricamente se si vuole ottenere una conferma della legge di Galileo relativa al moto di caduta della pallina.

È quello che ci proponiamo adesso con la serie di esperimenti che ci accingiamo a presentare.