Note sul codice binario

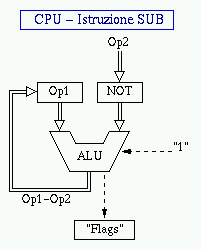
Complemento ad 1

Sotto il termine di complemento ad 1 di un numero binario si intende la differenza tra la configurazione di tutti '1' del codice ed il numero dato.
Il complemento ad 1 di 'A' e' simbolicamente indicato dall'apice 1 che precede la variabile 'A'; es: 1A

Per il calcolo si procede nel modo indicato dalla definizione.
Es: sia A = '0110 1101' la configurazione binaria di cui si vuole calcolare il complemento a 1: 

       1111 1111 -       (configurazione con tutti i bit a '1')
       0110 1101 =       (A)
     ---------------
       1001 0010         (1A = complemento ad 1 di A)

Quindi: 1'0110 1101' = '1001 0010'.
Da notare che non e' un caso particolare che il risultato coincida con la configurazione negata di A (not A). Infatti vale sempre la relazione:

1A = not(A)
pertanto, calcolare il complemento ad 1 di 'A' equivale a dire di calcolare la negazione di 'A'.
Cio' deriva direttamente dal fatto che sottrarre il bit 'x' da 1, da' come risultato 'x' negato, ossia not(x).
Ritorna a inizio pagina

Complemento a 2

Il complemento a 2 di un numero, e' uguale alla sua sottrazione da 2N, dove con 'N' si e' indicato il numero di bit impiegati per la rappresentazione del codice.
Il numero da complementare deve essere minore di 2(N-1)
Il complemento a 2 di 'A' e' simbolicamente indicato dall'apice 2 che precede la variabile 'A'; es: 2A
In definitava: 2A = 2N - A

Es:

Per il calcolo si procede nel modo indicato dalla definizione.
Es: sia A = '0110 1101' la configurazione binaria di cui si vuole calcolare il complemento a 2: 

       1 0000 0000 -       (configurazione corrispondente a 28)
         0110 1101 =       (A)
     -----------------
         1001 0011         (2A = complemento a 2 di A)

Non e' affatto casuale che il complemento a 2 di un numero sia maggiore di 1 del complemento a 1 dello stesso numero.
Infatti 2N = '1 0000 0000' = '1111 1111' + 1
Quindi

2A = 2N - A = 100000000 - A =
= (11111111 + 1) - A = (11111111 - A) + 1 = 1A + 1
C.V.D. #
Uno dei metodi di rappresentazione di numeri negativi e' proprio la rappresentazione in complemento a 2, tramite la quale e' possible trasformare una sottrazione binaria in una somma.
Per esempio e' dimostrabile che la differenza
A - B
puo' essere sempre ricondotta alla somma
A + 2B

Analogamente la somma

A + (-B)
equivale alla somma
A + 2B

Il bit di peso maggiore o 'Most Significant Bit' (MSB) e' riservato al segno del numero rappresentato e' viene quindi chiamato bit di segno.
Il bit di segno = 1, indica che il numero e' negativo. Per risalire al numero rappresentato, e' sufficiente ricalcolare il complemento a 2 dell'intero numero (compreso il bit di segno).
Infatti vale la proprieta' che 2(2A) = A
Per convincersi: 2(2A) = 2N - (2N - A) = 2N - 2N + A = A

C.V.D. #

ECCEZIONE:
In precedenza ho detto che il valore del numero per cui calcolare il complemento a due deve essere < 2(N-1).
Cio' e' strettamente vero per la rappresentazione dei numeri positivi (che non devono essere complementati a 2), ma in realta' per la rappresentazione di un numero negativo e' ammesso il range fino a 2(N-1) compreso.
Ecco cosi' spiegato perche' un byte puo' rappresentare i valori compresi fra:

Per lo stesso motivo una word (2 byte) puo' rappresentare i valori compresi fra:

CPU: istruzione SUB Il vantaggio del complemento a 2 e' quello di velocizzare i calcoli effettuati dall'ALU (Aritmetic Logic Unit) posta all'interno della CPU (Central Processing Unit) nel calcolo delle differenze fra valori.
La rete di ingresso dell'ALU e' molto veloce ad effettuare il complemento a 1 dell'operando da sottrarre (sottraendo) eseguendo una negazione di esso, dopidiche' l'ALU effettua l'operazione di somma tra
  • il primo operando (minuendo)
  • la negazione del sottraendo
  • il valore '1' preventivamento inserito nell'ingresso del riporto (CI - Carry Input)

Ritorna a inizio pagina

Confronti e sottrazioni

Nel Linguaggio Macchina 80x86 e' prevista l'istruzione CMP per eseguire confronti fra operandi di 8 o 16 bit.
L'istruzione CMP opera come SUB, cioe' esegue un'operazione di sottrazione senza, pero', modificare l'operando destinazione, ma con il solo effetto di modificare il registro dei flags.
Il test successivo di quali flag siano settati, completa l'operazione di confronto, con l'effetto di eseguire salti condizionati all'interno del codice macchina (o del programma assembler).

Di seguito, dopo una panoramica sulle convenzioni utilizzate si esaminano le diverse situazioni che possono capitare durante il confronto di operandi:

Convenzioni utilizzate

Nel seguito ho utilizzato i seguenti simboli:
Flag Nome Significato
CF Carry Flag 1 = Riporto per l'operazione successiva
BF Borrow Flag 1 = Prestito per l'operazione successiva
SF Sign Flag 1 = l'operando e' negativo
ZF Zero Flag 1 = l'operando e' nullo
OF Overflow Flag 1 = 'trabocco' del risultato
C Indica la colonna del Carry
S Indica la colonna del segno

N.B. - Sebbene che il BF non esista esplicitamente nel registro dei flags della CPU 80x86, l'ho voluto ugualmente prendere in considerazione per il fatto che nelle operazioni di sottrazione e di confronto, il CF assume il significato di BF.

N.B. - La condizione di overflow (OF=1) e' data dalla presenza di riporto sulla colonna del bit del segno o del bit del carry ma non in entrambe.
In altri termini non c'e' condizione di overflow (OF=0) se non c'e' riporto su nessuna delle due colonne, oppure se il riporto avviene su entrambe.

Qualche esempio potra' chiarire meglio le idee...

Esempio 1: Somma di 01010011 e 00110000

         C S
           111             (riga dei riporti)
           0101 0011 +     (1° operando)
           0011 0000 =     (2° operando)
       ---------------     
           1000 0011       (risultato)
In questo caso si verifica la condizione di Overflow, poiche' c'e' un riporto sulla colonna del bit di segno e non c'e' sulla colonna del bit di carry. Infatti interpretando gli operandi come signed, si avrebbe che 83+48=-125.
Interpretando la stessa operazione con operandi unsigned, il risultato sarebbe corretto: 83+48=131.

Esempio 2: Somma di 01010011 e 00101010

         C S
                 1         (riga dei riporti)
           0101 0011 +     (1° operando)
           0010 1010 =     (2° operando)
       ---------------     
           0111 1101       (risultato)
La condizione di overflow non e' verificata, poiche' non ci sono riporti ne' sulla colonna del bit del segno, ne' del bit di carry.
Il risultato risulta sempre corretto, sia interpretando gli operandi signed che unsigned. Infatti si ha: 83+42=125.

Esempio 3: Somma di 10101101 e 11010000 

         C S
         1                 (riga dei riporti)
           1010 1101 +     (1° operando)
           1101 0000 =     (2° operando)
       ---------------     
           0111 1101       (risultato)
Il risultato e' affetto da Overflow, poiche' risulta che -83+(-48)=+125.
Infatti si ha riporto solo sulla colonna del bit di carry e non del bit di segno. Interpretando l'operazione con operandi unsigned, servono almeno 9 bit per rappresentare il risultato, poiche' il bit di carry e' posto ad 1.
In tal caso si avrebbe 173+208=381.

Esempio 4: Somma di 10101101 e 11010110 

         C S
         1 1111 1          (riga dei riporti)
           1010 1101 +     (1° operando)
           1101 0110 =     (2° operando)
       ---------------     
           1000 0011       (risultato)
Il risultato non e' affetto da Overflow poiche' c'e' riporto sia sulla colonna del bit di segno che del bit di carry.
In questa situazione risulta che -83+(-42)=-125.
Interpretando gli operandi unsigned, per rappresentare il risultato occorrono 9 bit: 173+214=387.

Esempio 5: Somma di 10101101 e 00101010 

         C S
            1 1            (riga dei riporti)
           1010 1101 +     (1° operando)
           0010 1010 =     (2° operando)
       ---------------     
           1101 0111       (risultato)
Il risultato non e' affetto da Overflow poiche' non c'e' riporto ne' sulla colonna del bit di segno ne' del bit di carry.
In questa situazione risulta che -83+42=-41.
Anche interpretando gli operandi unsigned, il risultato risulta corretto: 173+42=215.

Esempio 6: Somma di 01010011 e 11010110 

         C S
         1 1 1  11         (riga dei riporti)
           0101 0011 +     (1° operando)
           1101 0110 =     (2° operando)
       ---------------     
           0010 1001       (risultato)
Il risultato non e' affetto da Overflow poiche' c'e' riporto sia sulla colonna del bit di segno che del bit di carry.
In questa situazione risulta che 83+(-42)=41.
Interpretando gli operandi unsigned, per rappresentare il risultato occorrono 9 bit: 83+214=297.

Operandi con segno

1° caso: Op1=Op2:

ZF = 1 (sempre !)

2° caso: Op1>Op2:

3° caso: Op1<Op2:

Operandi senza segno

1° caso: Op1=Op2:

ZF = 1 (sempre !)

2° caso: Op1>Op2:

Op1-Op2 > 0   ==>   Op1+2Op2 = Op1+(2N-Op2) = 2N+(Op1-Op2) > 2N
                                 ==>   CF = 1
                                       BF = 0
                                       OF = ?
                                       SF = ?

3° caso: Op1<Op2:

Op1-Op2 < 0   ==>   Op1+2Op2 = Op1+(2N-Op2) = 2N+(Op1-Op2) < 2N
                                 ==>   CF = 0
                                       BF = 1
                                       OF = ?
                                       SF = ?
Ritorna a inizio pagina

Conclusioni

Riepilogo in una tabella i risultati ottenuti precedentemente, assieme alle istruzioni assembler che permettono di eseguire il controllo sul verificarsi o meno delle condizioni:

Condizione Flag di controllo Istruzioni assembler
Operandi Signed Operandi Unsigned Operandi Signed Operandi Unsigned
Op1 = Op2 ZF=1
ZF=1
JE
JE
Op1 != Op2 ZF=0
ZF=0
JNE
JNE
Op1 > Op2 SF=0F e ZF=0
BF=0 e ZF=0
JG
JA
Op1 >= Op2 SF=0F
BF=0
JGE
JAE
Op1 < Op2 SF!=0F
BF=1
JL
JB
Op1 <= Op2 SF!=0F o ZF=1
BF=1 o ZF=1
JLE
JBE

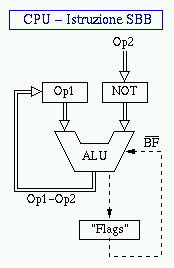
Poiche' la CPU 80x86 non possiede il BF (flag del prestito), il risultato del flag CF viene negato. In tal caso il CF porta l'informazione del BF, quindi il CF non rappresenta piu' un riporto ma un prestito.
Pertanto in tabella andrebbe indicato CF al posto di BF.

Nelle operazioni di somma, invece, la CPU 80x86 considera il CF come flag di riporto.

Dualmente all'addizione, anche per la sottrazione esistono 2 istruzioni:

CPU: istruzione SBB A livello di CPU, l'istruzione SBB viene eseguita effettuando la somma fra:
  • il primo operando (minuendo)
  • la negazione del secondo operando (sottraendo)
  • la negazione del BF (flag di prestito)

Per spiegare questa relazione basta fare delle sempili considerazioni, ricordando il complemento a 2:

BF=0   ==>   (Op1-BF)-Op2 = Op1+2Op2 = Op1+not(Op2)+1
BF=1   ==>   (Op1-BF)-Op2 = Op1-1+2Op2 = Op1-1+not(Op2)+1 = Op1+not(Op2)

==> (Op1-BF)-Op2 = Op1+not(Op2)+not(BF)

Ritorna a inizio pagina