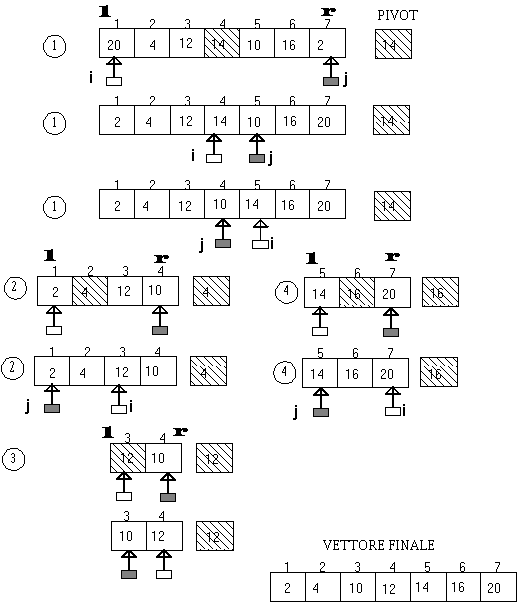
Il quicksort lavora partizionando l'array che deve essere ordinato e ricorsivamente ordina ogni parte (l'algoritmo è ricorsivo nel senso che si richiama su ciascun sotto-vettore fino a quando non si ottengono sotto-vettori di lunghezza 1: a questo punto il vettore di partenza risulta ordinato) . In Partition (figura sotto), un elemento dell'array è selezionato come valore pivot. I valori più piccoli del pivot sono sistemati a sinistra del pivot, mentre i più grandi a destra.
 
 

int function Partition (ArrayA, intLb, intUb);     begin     select a pivot from A[Lb]…A[Ub];     reorder A[Lb]…A[Ub] such that:     all values to the left of the pivot are <= pivot     all values to the right of the pivot are >= pivot return pivot position; end; procedure QuickSort (ArrayA, intLb, intUb);     begin     if Lb < Ubthen         M = Partition (A, Lb, Ub);         QuickSort (A, Lb, M – 1);         QuickSort (A, M + 1, Ub);     end;

In figura a), il pivot selezionato è 3. Gli indici sono a entrambi gli estremi dell'array. Un indice comincia sulla sinistra e seleziona un elemento che è più grande del pivot, mentre un altro indice comincia sulla destra e seleziona un elemento minore del pivot. In questo caso, i numeri 4 e 1 sono selezionati. Questi elementi sono allora scambiati, come mostrato in figura b). Questo processo si ripete finchè tutti gli elementi a sinistra del pivot sono <= del pivot, e tutti gli elementi alla destra del pivot sono >= del pivot. Quicksort ordina ricorsivamente i due sottoarray e alla fine risulterà l'array mostrato in figura c).
 
 

	Lb				Lb
b)	1	2	3	5	4

Come il processo avanza, può essere necessario muovere il pivot in modo che l'ordine corretto rimanga. In questa maniera quicksort segue nell'ordinare l'array. Se siamo fortunati il pivot selezionato sarà la media di tutti i valori, dividendo in maniera equa l'array. Se è questo il caso l'array è diviso ad ogni passo a metà, e Partition deve esaminare tutti e n gli elementi: la complessità sarà O(nlogn).
Per trovare un valore pivot, Partition potrebbe semplicemente selezionare il primo elemento (A[Lb]). Tutti gli altri valori dovrebbero essere comparati al valore pivot, e messi o a dx o a sx del pivot. Comunque, c'è un caso che fallisce miseramente. Si supponga che l'array è all'inizio in ordine. Partition selezionerà sempre il valore più basso come pivot e dividerà l'array con un elemento nella parte sx, e Ub-Lb elementi nell'altra. Ogni chiamata ricorsiva a quicksort diminuirà la grandezza dell'array. Perciò n chiamate ricorsive sranno richieste per fare l'ordinamento, risultando di complessità O(n²). Una soluzione a questo problema è selezionare casualmente un elemento come pivot. Questo renderebbe estremamente sfortunata l'occorrenza del caso pessimo.

Complessità del quicksort

Caso peggiore:

Ad ogni passo si sceglie un pivot tale che un sotto-vettore abbia lunghezza 0

n-1 attivazioni di quicksort
al passo k, si opera su un vettore lungo L = n-k

time(N) = n-1 + n-2 + ... + 2 + 1 = n*(n-1)/2 = O(n²)

Caso migliore:

Ad ogni passo si sceglie un pivot tale che il vettore si dimezzi (cioe' si emula il merge sort)

log₂ n attivazioni di quicksort
al passo k si opera su 2^k vettori di lunghezza L = n/2^k
quindi, il numero di confronti ad ogni livello è n.

Caso medio:

La scelta casuale del pivot rende probabile la divisione in due parti aventi circa lo stesso numero di elementi.

Pertanto, si ha la stessa complessità del caso migliore:

time = O(n*log₂ n)
 

Esempio: