Cenni sulla Complessità degli Algoritmi

La Teoria della complessità, che ha avuto un forte sviluppo intorno agli anni '70 si occupava appunto di:

- complessità di un problema;
- valutazione dell'efficienza degli algoritmi.

Un programma richiede spazio di memoria e tempo di calcolo.
Ci concentriamo su quest'ultimo per valutare la complessità dei programmi.

Esempio: C = A x B

Moltiplicazione di due matrici quadrate nxn di interi: per calcolare C[i,j] si eseguono 2n letture, n moltiplicazioni, n-1 addizioni ed 1 scrittura.

Per calcolare C: n²*(2n letture, n moltiplicazioni, n-1 addizioni ed 1 scrittura):

2n³ letture
n³ moltiplicazioni
n²*(n-1) addizioni
n² scritture

time(n) = 2n³+n³+n²*(n-1) +n² = 4*n³

Occorre tener presente che il tempo t dipende dai seguenti fattori:

• la macchina usata, intendendo con ciò l'hardware, il sistema operativo, il compilatore ed, in macchine multitasking, il carico;
• la configurazione dei dati in ingresso;
• la dimensione dei dati in ingresso.

Valutare la complessità degli algoritmi ci consente di scegliere tra loro quello più efficiente (a minor complessità).

La complessità dell'algoritmo viene espressa in funzione della dimensione delle strutture dati.

Esempio: algoritmo del generico problema P

timeAlg(P)(n)=2n

timeAlg(P)(n)=4*n3

Per esempio, avendo a disposizione un elaboratore che esegue 10³ operazioni al secondo, l'algoritmo risolutivo del problema P con ingresso di dimensione 10 impiega 1 sec., con ingresso di dimensione 20 impiega 1000 sec (17 min), con 30 10⁶ sec (>10giorni), con 40 10⁹ sec (>>10 anni)
 
 

Comportamento asintotico: notazione O     

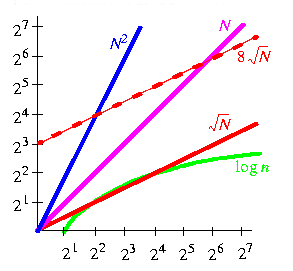
Individuare con esattezza la funzione time(n) è spesso molto difficile.

Spesso, però, è sufficiente stabilire il comportamento asintotico della funzione quando le dimensioni dell'ingresso tendono ad infinito (comportamento asintotico dell'algoritmo).
 

Definizione

Un algoritmo (programma) ha costo O(f(n)) (o complessità O(f(n)) ) se esistono opportune costanti a,b, n' tali che:

timeA(n) < a*f(n)+b per ogni n>n'.

Esempi:

3*n²+4*n+3 = O(n²), perché 3*n²+4*n-3 <= 4*n² per n>3.
time(n)=4*n³ = O(n³)

Si hanno così le suguenti:
 
 
 

Classi di complessità    

1) Complessità costante
O(1)
È posseduta dagli algoritmi che eseguono sempre lo stesso numero di operazioni indipendentemente dalla dimensione dei dati.
Es.: inserimento o estrazione dalla testa di una lista concatenata, ecc.

2) Complessità sottolineare
O(n ), con k<1 k
Es.:Ricerca binaria, o logaritmica, ecc.

3) Complessità lineare
O(n)
È posseduta dagli algoritmi che eseguono un numero di operazioni sostanzialmente proporzionale ad n. Es.: ricerca sequenziale, somma di numeri di n cifre, merge di due file, ecc.

4) Complessità n log n
O(n log n)
Es.: Algoritmi di ordinamento ottimi.

5) Complessità n^k , con k>=2
O(n^k)
Es.: Bubblesort ( O(n^2) ), moltiplicazione di due 2 matrici ( O(n^3) ), ecc.

6) Complessità esponenziale
Tutte le classi di complessità elencate precedentemente vengono genericamente considerate come polinomiali. Esse sono caratterizzate dal fatto che la dimensione n non compare mai come esponente in alcun modo. Quando ciò avviene si parla invece di complessità esponenziale.
Es.: un algoritmo che debba produrre tutte le possibili stringhe lunghe n di k simboli avrà complessità O(k^n) cioè esponenziale.
L'algoritmo della Torre di Hanoi ha complessità O(2^n) (sono necessarie 2^n - 1 mosse).
È necessario guardare con particolare diffidenza agli algoritmi dotati di complessità esponenziale, perché possono richiedere dei tempi di esecuzione proibitivi (se non addirittura astronomici) anche per valori relativamente piccoli di n ed indipendentemente dalla velocità dell'elaboratore.
Purtroppo esistono molti problemi, anche di interesse pratico, per i quali non si conoscono ancora algoritmi non esponenziali (problemi intrattabili). Es.: problema del commesso viaggiatore.
Un problema è computazionalmente trattabile se esiste un algoritmo efficiente che lo risolve; altrimenti il problema è computazionalmente intrattabile.
Un algoritmo si dice efficiente se il suo tempo di esecuzione è limitato superiormente da una funzione
polinomiale (funzione limitata superiormente da n^k per un opportuno fissato intero k).

Esempi:

log n ---> complessità logaritmica
c1*n+c2 ---> complessità lineare
n²+n ---> complessità quadratica
n^k +c3*n ---> complessità polinomiale
2ⁿ+n ---> complessità esponenziale

Dato un problema P e due algoritmi A1 e A2 che lo risolvono siamo interessati a determinare quale ha complessità minore (è "il migliore" dal punto di vista dell'efficienza computazionale).

Esempio:

timeA1(n)=3n²+n

timeA2(n)=n²+10n

Per n>=5, timeA2(n)<timeA1(n). La complessità di A2 è minore per ingressi con dimensione maggiore di 5.

NB: non è detto che quel che vale per n "grande" valga anche per n "piccolo". Ma ci interessa che un algoritmo sia efficiente per n grande (se n "piccolo", c'è poca differenza, e comunque ogni algoritmo va bene... o quasi!)
 

Definizione:

Dato un problema P e due algoritmi A e B che lo risolvono con complessità timeA e timeB, diciamo che A è migliore di B nel risolvere P se:

(1) timeA=O(timeB)

(2) timeB non è O(timeA)
 

Nell'esempio sopra, timeA1=O(timeA2) e viceversa: A1 e A2 hanno entrambi comportamento asintotico quadratico (O(n²)). Sono dunque equivalenti dal punto di vista del costo computazionale.

Controesempio:

timeB1(n)=3n²+n

timeB2(n)=n*log n
 
 

Comportamento asintotico: notazione W    

Definizione

timeA(n) > c*g(n)

per un numero infinito di valori di n.

Esempio

3n²+n = W(n²) (ma anche W(n) e W(n*log n))

W(g(n)), rappresenta un limite inferioreal comportamento di una funzione.

Si ha una valutazione esatta del costo di un algoritmo quando le due delimitazioni O(f(n)) e W(f(n)) coincidono.
 
 

Delimitazioni alla complessità di un problema    

Un problema ha delimitazione superiore O(f(n)) alla sua complessità se esiste almeno un algoritmo di soluzione per il problema con complessità O(f(n)).

Un problema ha delimitazione inferiore W(g(n)) alla sua complessità se è possibile dimostrare che ogni algoritmo di soluzione per il problema ha complessità almeno W(g(n)).

Note:

L'idea di fondo è che se esiste almeno un algoritmo di complessità O(f(n)), il problema non potrà essere più complesso di questo: altrimenti, non avremmo potuto trovare neppure questo algoritmo. Quindi, O(f(n)) è senz'altro una delimitazione superiore alla complessità del problema P.
Questo non significa che P abbia davvero complessità O(f(n)): se troviamo un nuovo algoritmo per risolvere P, la cui complessità O(h(n)) è minore di O(f(n)), automaticamente O(h(n)) diverrà il nuovo limite superiore alla complessità di P.
Viceversa, affermare che W(g(n)) è un limite inferiore alla complessità del problema significa essere certi che sarà impossibile trovare un algoritmo migliore. Perciò, per affermarlo bisogna dimostrare che tutti i possibili algoritmi che risolvono P hanno almeno questa complessità.

Infatti, se la complessità del problema è W(f(n)), significa che meno di f(n) non si potrà mai fare; e quindi i migliori algoritmi avranno appunto complessità O(f(n)) [algoritmi peggiori potrebbero avere complessità superiore, ma ovviamente cercheremo di evitarli].

In particolare diremo che un problema ha complessità:

lineare quando ogni algoritmo che lo risolve ha complessità O(n) e W(n)
polinomiale quando ogni algoritmo che lo risolve ha complessità O(n^k) e W(n^k), con k>1.

Istruzione dominante    

Permette di semplificare in modo drastico la valutazione della complessità.
 

Definizione

Dato un algoritmo (o programma) A il cui costo di esecuzione è t(n), un'istruzione di A è detta dominante quando, per ogni intero n, essa viene eseguita (nel caso di input con dimensione n) un numero d(n) di volte tale che:

per opportune costanti a, b.

In pratica, una istruzione dominante viene eseguita un numero di volte proporzionale al costo dell'algoritmo.

Perciò, se esiste un'istruzione dominante, la complessità dell'algoritmo si riconduce a quella legata all'istruzione dominante, ossia la complessità dell'algoritmo è O(d(n)).

Esempio: ricerca esaustiva di un elemento in un vettore di dimensione N

boolean ricerca (vettore vet, int el){
int i=0; boolean T=falso;

while (i<N) { /* (1) */

if (el==vet[i]) /* (2) */ T=vero;
i++;

}

return T;

Le istruzioni (1) e (2) sono quelle dominanti, e vengono eseguite rispettivamente N+1 volte (per i=0..N) e N volte (per i=0..N-1): dunque il costo è lineare.

Esempi su vettori: Ricerca del valore minimo e massimo di un vettore

int minimo (vettore vet) {
int i, min;

for (min = vet[0], i = 1; i < N; i ++)
if (vet[i]<min) /* istr. dominante */
min = vet[i];

return min;
}
 

int massimo (vettore vet) {
int i, max;

for (max = vet[0], i = 1; i < N; i ++)
if (vet[i]>max) /* istr. dominante*/
max=vet[i];

return max;
}

Sia per la ricerca del minimo che del massimo, l'istruzione dominante viene eseguita N-1 volte.

Perciò entrambi gli algoritmi hanno un costo O(n), se n è la dimensione del vettore.
 
 

Dipendenze dai dati d'ingresso    

Molto spesso il costo dell'esecuzione di un algoritmo dipende non solo dalla dimensione dell'ingresso, ma anche dai particolari valori dei dati in ingresso.

E' il caso tipico di molti algoritmi di ordinamento: se il vettore è già ordinato (o quasi), finiscono subito, mentre se è "molto disordinato" devono eseguire molti più passi.

Si distinguono diversi casi: caso migliore, caso peggiore, caso medio.

Di solito la complessità viene valutata nel caso peggiore (e talvolta nel caso medio).
 

Esempio: Per la ricerca sequenziale in un vettore il costo dipende dalla posizione dell'elemento cercato.

Caso migliore: l'elemento è il primo del vettore (un solo confronto)

Caso peggiore: l'elemento è l'ultimo o non è presente: l'istruzione dominante è eseguita N volte (N dimensione del vettore). Il costo è lineare.

OSSERVAZIONE.
Il caso peggiore è utile, ma non sempre significativo in pratica, perché solitamente è anche raro. Ha quindi senso cercare di capire cosa succede "di solito", in un caso "medio".

Caso medio: ciascun elemento sia equiprobabile

L'elemento cercato potrebbe essere il primo ( 1 confronto), o il secondo (2 confronti), ..., oppure l'ultimo ( N confronti)

time(N) = S(i=1..N) Prob(el(i)) * i = S(i=1..N) (1/N) * i = (N+1)/2

Informazioni e complessità    

Il risultato precedente dipende dal fatto che non avevamo particolari informazioni da sfruttare per "guidare" la ricerca.

Invece, sapendo che il vettore è ordinato, la ricerca può essere ottimizzata.

Esempio: Ricerca binaria

Rispetto alla ricerca esaustiva, la tecnica di ricerca binaria consente a ogni passo di dimezzare il vettore.

Si confronta l'elemento cercato el con quello mediano del vettore, V[med].
Se el==V[med], fine della ricerca (trovato=true).
Altrimenti,
se il vettore ha almeno due componenti
(first <last):

se el<V[med], ripeti la ricerca nella prima metà del vettore (indici da first a med-1);
se el>V[med], ripeti la ricerca nella seconda metà del vettore (indici da med-1 a last).

Calcolo della complessità della ricerca binaria    

Come per la ricerca sequenziale, il costo dipende dalla posizione dell'elemento cercato.

Però, sarà più semplice trovarlo!

Caso migliore: l'elemento cercato è il primo con cui ci confrontiamo nel vettore (quello mediano): dunque, si fa un solo confronto

Caso peggiore: l'elemento cercato non è nel vettore.

Il ciclo è ripetuto finché ci si riduce ad un vettore mono-dimensionale (first==last).

Poiché ad ogni passo il vettore si dimezza, si hanno al più k passi (con k finito e proporzionale a log₂N):

time(N) = S(i=1..k) 1 = k = (log₂ N)