Per semplificare il discorso formuliamo le seguenti ipotesi:

• Che l’orbita del Terra sia perfettamente circolare
• Che il movimento della Terra nella sua orbita sia costante
• Che l’asse di rotazione della Terra sia perpendicolare all’equatore celeste

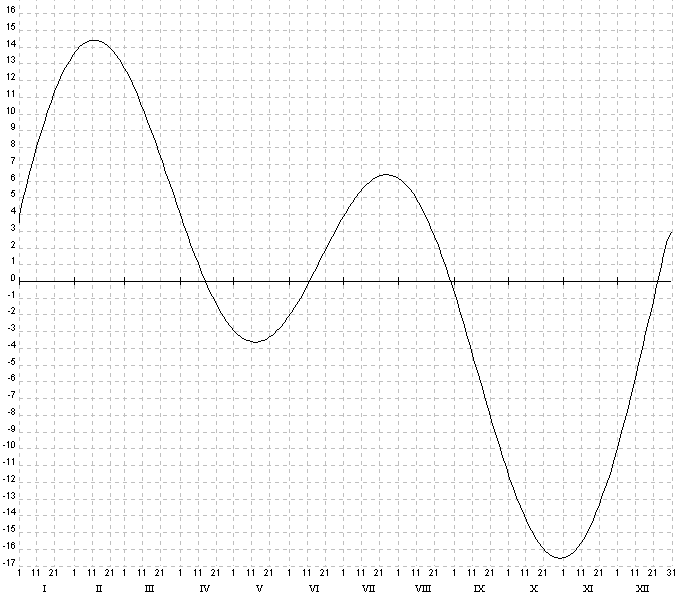
Questo "Sistema" convenzionale ci fornisce il Tempo Medio che è il principio di riferimento della meccanica dei nostri orologi. Avremo ore tutte uguali

Il Tempo Vero, quello della Meridiana , è riferito alla realtà delle cose considerando quindi quanto segue :

Che l'asse di rotazione della Terra intorno al Sole non è perpendicolare all’equatore celeste,  ma inclinato di 23° 27’  

Che  che l’orbita della Terra non è  perfettamente circolare,  ma  ellittica;                                                                

Che il movimento della Terra nella sua orbita  non è costante in quanto accelera quando si avvicina al Sole (Perielio)  e decelera quando se ne allontana (Afelio).

Prima cosa da considerare quindi è che il variare della velocità di rivoluzione della Terra causa il variare della durata del giorno, avremo quindi giorni veri più lunghi e più corti rispetto a giorni medi tutti uguali. Le differenze tra questi   due sistemi si possono rappresentare con un grafico, una curva sinusoide denominata Equazione del Tempo.

La curva mostra che solo in quattro momenti all’anno il tempo vero ed il tempo medio coincidono. Possiamo inoltre notare che le differenze possono variare da + 14 minuti circa intorno al 10/14 Febbraio (sole in anticipo) e –16 minuti circa intorno al 23 di Novembre (sole in ritardo).

Concludendo sottraendo o addizionando i dati forniti dall’equazione del tempo potremo apportare all’ora vera quella prima correzione che ci permette di risalire all’ ora media.

La seconda correzione che dobbiamo considerare e’ quella relativa all’introduzione nel nostro sistema di computo del tempo dei Fusi Orari.

Il nostro Fuso di Riferimento è il Primo ad Est , passa sulI’ Etna ed è a 15° Est dal fuso Universale di Greenwich. Il Sole impiega un’ora per passare da un fuso all’altro (15°), quindi 4 minuti per percorrere un grado (60: 15 =4).

Pensiamo ad una meridiana posta sull’ Etna, alle ore 12 in punto del nostro orologio del 1 Gennaio, l’ombra dello gnomone segnerà le 12 meno il dato fornito dall’equazione del tempo che è di circa 4 minuti di anticipo . La meridiana anticipa di 4 Minuti. Ora spostiamo la meridiana e la portiamo in un altro luogo con longitudine 11° Est , quindi 4° in meno rispetto al meridiano dell’Etna. Se e’ vero che il Sole per percorrere un grado nell’eclittica impiega 4 minuti e’ anche vero che dopo essere passato sul Meridiano dell’ Etna impiega 16 minuti per passare sul meridiano del nuovo luogo. Quindi considerando di rilevare l’orario della meridiana alle ore 12.00 del 1 Gennaio dobbiamo tenere conto anche di questa differenza.

In pratica

La Prima correzione varia giorno per giorno mentre la seconda correzione e’ fissa ed e’ anche chiamata Costante Locale. La terza correzione si applica quando è in vigore l’ora estiva. (togliere 1 ora)

Spesso le meridiane hanno anche una funzione calendariale e qui entra in ballo l’inclinazione dell’asse terrestre.

L’estremità dell’ombra dello gnomone infatti fornisce indicazione della data ovvero del periodo dell’anno nel quale viene fatta l’osservazione.

Allo stesso momento del giorno, ad esempio a mezzogiorno solare, l’estremità dell’ombra dello gnomone sarà proiettata in posizioni diverse del quadrante a seconda della stagione.

Consideriamo una meridiana verticale, nel periodo invernale quando il Sole è più basso all’orizzonte l’ombra sarà più corta e la sua estremità sarà collocata più in alto nel quadrante. La lunghezza minima si ha al solstizio d’inverno, il 21 Dicembre. Al contrario, al solstizio d’Estate , 21 Giugno, il sole raggiunge la sua posizione più elevata sull’orizzonte e la lunghezza dell’ombra sarà massima. Una posizione intermedia si avrà agli equinozi di primavera e di Autunno (21 marzo e 23 Settembre).

Se ora consideriamo non più il solo momento del mezzogiorno, ma per ciascuna ora vedremo lo scorrere dell’ombra lungo l’intero arco del giorno, si disegnano così sul quadrante tre linee :

un’iperbole superiore (solstizio d’inverno)

un’iperbole inferiore (solstizio d’estate)

una retta intermedia coincidente al momento dei due equinozi.

Allo stesso modo si possono indicare le curve corrispondenti ai giorni di passaggio da un segno zodiacale all’altro oppure una linea corrispondente ad una certa data anniversario.

Equazione del Tempo