Individuare una retta che attraversi il cerchio in modo da bisecare
esattamente le aree dello Yin e dello Yang.
(La monade è un cerchio diviso da due semicirconferenze opposte
il raggio delle quali è metà di quello del cerchio)
La soluzione presuppone una dimostrazione grafica.

Risolto da Daniele di Stanio (31-08-00 16:52)

La soluzione è sotto a fine pagina....

bye

 

 

 

 

 

 

 

 

 

 

 

Soluzione:

Il disegno ed il testo sono quelli forniti da Daniele:

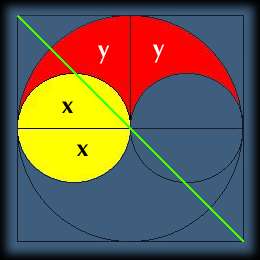
Ciascuna delle due parti del tao è equivalente a 2x + 2y
Quindi è possibile dividerla in due parti uguali con la retta verde
poichè la retta verde divide esattamente a metà la figura x + y.
X + y è la metà della parte nera del tao poichè: 2x + 2y = 2(x + y).
La parte bianca verrà divisa anch'essa essendo simmetrica alla parte nera rispetto al centro della circonferenza.