E' possibile costruire una ellisse piegando un
foglio di carta più
volte
(un numero teoricamente infinito di volte).
Quale
forma dovrà avere e come dovrà essere piegato il foglio
di carta?
E' richiesta una dimostrazione geometrica.
_______
It's
possible to obtain an ellipse folding a paper sheet repeatedly over
and over again.
Which is the shape of the paper sheet?
In wich way will be folded it?
A demonstration is required.
Risolto da:
Solved by:
Michael R. Straight
(26-12-01 20:19)
la soluzione è
sotto:
the solution is below:
bye
Soluzione inviata
da Michael:
Solution sent by Michael:
Start with a paper
in the shape of a circle.
Make a dot anywhere between the edge of the paper and the center.
Fold the edge of the paper to the dot.
Repeat from another point on the edge of the paper, folding it to the
dot. When enough points on the edge are folded to the dot, a shape like
an ellipse is formed.
Si inizia con un
foglio di carta di forma ciorcolare.
Si esegue un punto tra il bordo del foglio ed il centro.
Si piega il bordo del foglio fino a toccare il punto.
Si ripete da un'altra posizione del bordo del foglio, piegandolo fino
a toccare il punto.
La forma di un ellisse si otterrà con un sufficiente numero di
piegature
(che dovrebbero essere infinite)
Waiting for a geometrical
proof (Below, a good help)
Si attende la dimostrazione geometrica (sotto, un notevole aiuto)
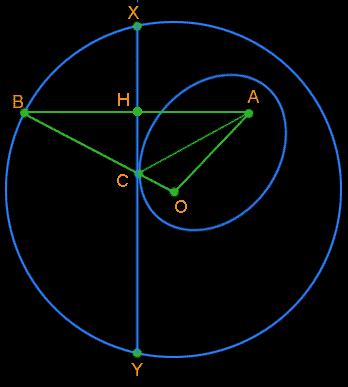
La dimostrazione
è stata inviata da Salomone Chei
(16-02-02 03:32)
Il triangolo ABC
è isoscele poichè XY è perpendicolare ad AB
e H è il punto medio di AB; quindi AC = BC, ma OB = raggio =
OC + BC da cui raggio = OC + AC. Questo succede per ogni punto B sulla
circonferenza quindi il punto C sta su un ellisse di fuochi O e A.
The
ABC triangle is isosceles because XY is perpendicular to AB and H is
the mid point of AB; thus AC = BC, but OB = radius = OC + BC therefore
radius = OC + AC. That happens for each point of the circumference therefore
the point C belongs to an ellipse with focus in O and A.
bye