Una formazione quadrata di cadetti, di 50 metri di lato, marcia a passo
costante. La mascotte della compagnia, un piccolo terrier, parte dal
centro dell'ultima fila (A) e trotterella in avanti in linea retta sino
al centro della prima riga (B), poi si gira e torna al centro dell'ultima (A).
Nell'istante in cui il cane ritorna in A, i cadetti hanno percorso
esattamente 50 metri.

Se il cane trotta a velocità costante e non perde tempo nel girarsi,
quanti metri avrà percorso?

(precisione richiesta: almeno 2 decimali
...necessaria breve ma esauriente dimostrazione)

Risolto brillantemente da Daniele di Stanio
17/08/2000 17:50

la soluzione è sotto a fine pagina...

 

 

 

 

 

 

 

 

 

 

Soluzione:

Daniele ha inviato una soluzione diversa da quella standard ed è proprio la sua, semplice e corretta, che viene qui proposta
(con l'aggiunta della grafica e di qualche chiarimento ulteriore):

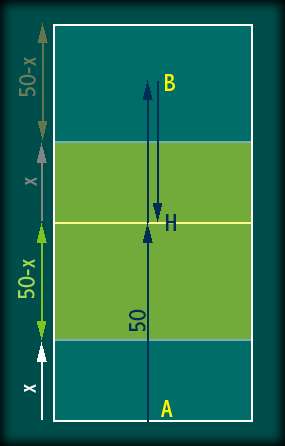
Sia x la distanza percorsa dai cadetti quando il cane ha percorso 50 m.
Osserviamo che i due tratti HB + BH del cane, vengono coperti mentre i cadetti avanzano di 50 - x.
Il punto B deve essere mediano rispetto al tratto 50 - x (In B il cane incontra la prima fila dei cadetti )
Ne segue che la distanza totale percorsa dalla mascotte sarà:

50 + x + (50-x)/2 + (50-x)/2 +x = 100 + x

E' quindi possibile impostare la proporzione:

100 +x : 50 = 50 : x
da cui:
x(^2) + 100x - 2500 = 0

Considerando la sola soluzione positiva dell'equazione quadratica si ottiene
x = 20,710678...
per cui la soluzione richiesta è:
100 + x = 100 + 20,71 = 120,71