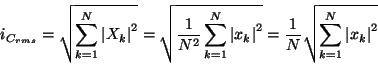Nota sul comando fft del MATLAB

Secondo l'help del comando fft del MATLAB, se abbiamo un vettore con componenti, il comando fft() calcola il vettore tale che:

$$X(k)=\sum ^{N}_{n=1}x(n)e^{-j2\pi (k-1)\frac{n-1}{N}}$$

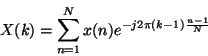
Il comando ifft(), invece, calcola il vettore tale che:

$$x(n)=\frac{1}{N}\sum ^{N}_{k=1}X(k)e^{j2\pi (k-1)\frac{n-1}{N}}$$

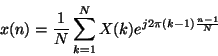
Sono formalmente identiche alle usuali formule per il calcolo della DFT e della IDFT, a meno del fattore di scala , che solitamente si trova nell'espressione della DFT. Nel seguito si fa implicitamente riferimento alla seguente notazione:

$$X_{k}=\frac{1}{N}x_{k}$$

dove con intendiamo i coefficenti della DFT e con i coefficenti del comando fft.

Per esempio nel calcolo del valore efficace si ha:

$$i_{C_{rms}}=\sqrt{\sum ^{N}_{k=1}\left\vert X_{k}\right\vert... ...rac{1}{N}\sqrt{\sum ^{N}_{k=1}\left\vert x_{k}\right\vert ^{2}}$$