Analisi Complessa

Lezione del 12 novembre 2009-11-12

In questa lezione, estendiamo il campo dei numeri reali con . In particolare, diamo ai numeri complessi le operazioni di somma, prodotto e divisione.

Ricordiamo che un numero complesso è un oggetto nella forma

Dove a e b sono numeri reali e

Ricordiamo che a e b si dicono, rispettivamente, parte reale e parte immaginaria del numero complesso

1.Somma di due numeri complessi

Siano e due numeri complessi. Poniamo

La somma di due numeri complessi ha un significato geometrico, E’ la diagonale del parallelogramma individuato dai due punti che rappresentano e nel piano di Gauss-Argand.

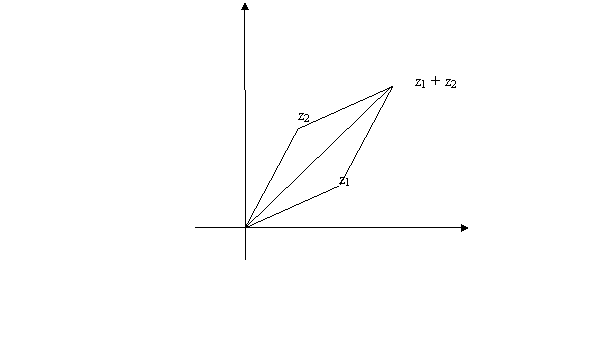
Rappresentazione geometrica della somma di due numeri complessi

Esempio

Allora

z

. I due numeri complessi in questo caso si dicono coniugati.

Due numeri complessi sono coniugati se hanno la stessa parte reale e parte immaginaria opposta

Esercizio sia un numero complesso. Trovare il numero coniugato di z.

Sia un numero complesso, Il coniugato di si indica con

Sia poniamo

La differenza di due numeri complessi è immediata. Osserviamo infatti che non è che

Prodotto di due numeri complessi. Siano

Il prodotto si fa nella maniera naturale

Esempio 2

Quindi, in generale si ha

Inverso di un numero complesso. Sia L’inverso di z –che si indica con -è tale che

Se allora . Infatti

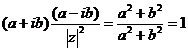
A questo punto è facile definire il quoziente di due numeri complessi