Si chiama simmetria ortogonale assiale di asse r una corrispondenza biunivoca del piano in sé stesso che ad ogni punto P associa il punto che si ottiene con le seguenti condizioni:

1)

2) oppure 

Per trovare l’equazione di simmetria di un asse di simmetria bisogna trasformare le due condizioni algebricamente.

Per trovare le coordinate dell’immagine di un punto bisogna sostituire le cordinate del punto iniziale (P) alla x e alla y dell’equazione di simmetria.

Per trovare la legge dell’immagine di una retta bisogna sostituire i valori di x e di y dell’equazione di simmetria inversa alla legge della retta iniziale .

 

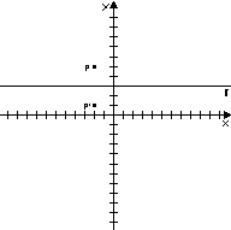
Simmetria con asse di simmetria parallelo all’asse X

 

quindi

   

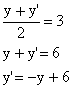
Trovo y'

 

 Equazione della simmetria

 

 Equazione della simmetria inversa

 

Esempio 1 (simmetria di un punto):

 

Cordinate di

 

Esempio 2 (simmetria di una retta):

 

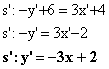
 Simmetria con asse di simmetria parallelo all’asse Y

 

 

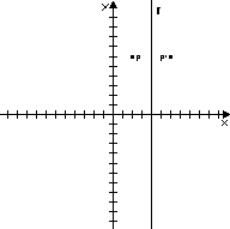
quindi

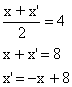    Trovo

 

 Equazione della simmetria

 

 Equazione della simmetria inversa

 

Esempio 1 (simmetria di un punto):

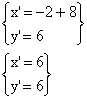
Cordinate di

 

Esempio 2 (simmetria di una retta):

 

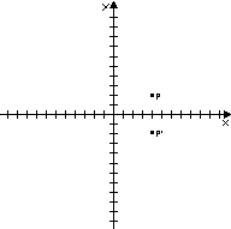
Simmetria avente l’asse X come asse di simmetria

 

Questa simmetria ha una sua equazione della simmetria che e:

 

 

 Equazione della simmetria inversa

 

Esempio 1 (simmetria di un punto):

 

Cordinate di

Esempio 2 (simmetria di una retta):

 

Simmetria avente l’asse Y come asse di simmetria

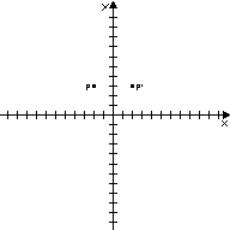
Questa simmetria ha una sua equazione della simmetria che e:

 

 

 Equazione della simmetria inversa

 

Esempio 1 (simmetria di un punto):

 

Cordinate di

 

Esempio 2 (simmetria di una retta):

 

       Simmetria avente la bisettrice del 1° e 3° quadrante come asse di simmetria

 

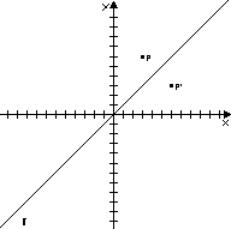
Questa simmetria ha una sua equazione della simmetria che e:

 

 Equazione della simmetria inversa

 

Esempio 1 (simmetria di un punto):

 Cordinate di

 

Esempio 2 (simmetria di una retta):

 

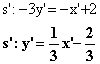
Simmetria avente la bisettrice del 2° e 4° quadrante come asse di simmetria

 

 

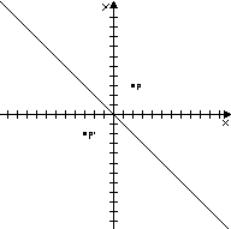
Questa simmetria ha una sua equazione della simmetria che e:

 

 

 Equazione della simmetria inversa

 

Esempio 1 (simmetria di un punto):

 

Cordinate di

 

Esempio 2 (simmetria di una retta):

 

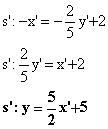
Simmetria con asse di simmetria obliquo

 

 

 

 

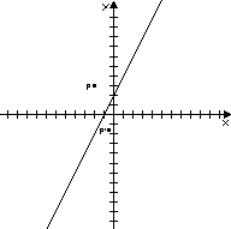
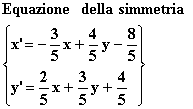
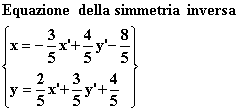
 Da ricordare:        

Due rette sono ortogonali se il coefficiente angolare 

(k) di una retta è l’antireciproco dell’altra retta

 

Condizione 1)         e

                                               Quindi

                              

 

   Condizione 2)       e

                                               Quindi

                              

 

Mettendo le due condizione in un sistema si ottiene:

   

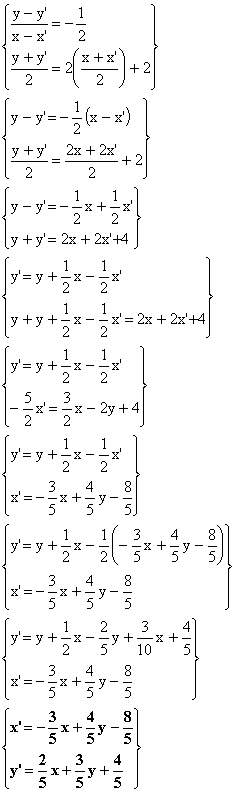
Esempio 1 (simmetria di un punto):

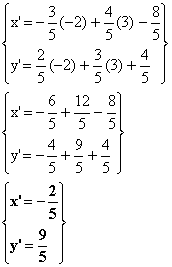
Cordinate di

 

Esempio 2 (simmetria di una retta):

 

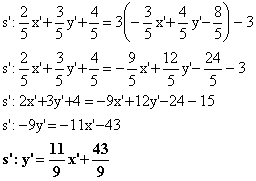
Torna all'inizio                               Torna al Sommario