Definizione: Si chiama similitudine piana un’affinità che trasforma una circonferenza in una circonferenza.

Si può dimostrare la seguente proprietà che caratterizza le similitudini piane:

Teorema: Un’affinità è una similitudine se e soltanto se è costante il rapporto di due segmenti corrispondenti (rapporto di similitudine).

E’ inoltre importante il seguente teorema:

Teorema: In un sistema cartesiano ortogonale, le equazioni di una similitudine sono del tipo:

(1)      oppure del tipo   (2) 

dove k, ©, p, q sono costanti reali e k>0.

Commento-dimostrazione: a tale risultato si giunge a partire dalle equazioni di un’affinità

(3)

 

imponendo che l’immagine della circonferenza di equazioni X +Y =1 sia ancora una circonferenza; ciò si verifica se e soltanto se valgono le seguenti relazioni:

(*)  

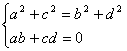
che rappresentano le condizioni analitiche cui debbono soddisfare i coefficienti di un’affinità per essere una similitudine.

Posto k =  , si può scrivere a = kcos e c = ksen ; sostituendo le espressioni di a e c appena trovate nel sistema (*) si ottiene il sistema equivalente:

(**)  

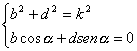
Risolvendo tale sistema rispetto a b e d si ottengono le soluzioni:

       e      

Sostituendo nelle (3) ad a, b, c, d i valori ora trovati si ottengono le (1) e le (2).

Il numero reale positivo k =  =   che compare nelle equazioni (1) e (2) di una similitudine prende il nome di rapporto di similitudine.

Esso rappresenta il rapporto costante tra segmenti corrispondenti in una similitudine (tale proprietà può essere facilmente dimostrata).

Poiché risulta a = kcos© e c = ksen©, le equazioni della similitudine assumono la forma:

(1')              oppure             (2')  

essendo k =  il rapporto di similitudine.

Nelle (1') risulta  det(A) = a >0, mentre nelle (2') risulta  det(A) = -a <0. Pertanto le (1') rappresentano le equazioni di una similitudine diretta di rapporto k = , mentre le (2') rappresentano le equazioni di una similitudine inversa di rapporto k = .

 

Qui di seguito elenchiamo le proprietà invarianti per una similitudine:

1.      Tutte le proprietà invarianti per un’affinità.

2.      Ampiezza degli angoli.

Inoltre una similitudine conserva il rapporto tra segmenti corrispondenti. Tale rapporto costante k, come già detto, prende il nome di rapporto di similitudine. Da questa proprietà discende in modo ovvio che in una similitudine è costante il rapporto dei perimetri di due figure corrispondenti (dette figure simili) e tale rapporto è pari al rapporto di similitudine k.

 

Elenchiamo alcune proprietà che non sono invarianti per una similitudine:

1.      Distanza fra due punti (o equivalentemente, lunghezza di un segmento).

2.      Direzione.

Per quanto detto si può affermare che le similitudini non conservano le dimensioni (poiché non conservano la distanza) ma conservano la forma (poiché conservano l’ampiezza degli angoli).

 

PROF. MICHELE FARINA

 

Torna all'inizio                           Torna al Sommario