Si definisce polare di un punto P(x ₁,y₁) , nella polarità definita da una conica Γ (circonferenza, parabola, ellisse, iperbole), la retta r (del piano π al quale appartengono Γ e P) la cui equazione si ottiene operando nell’equazione della conica le seguenti sostituzioni:

x ²   con  x ¹ x,         y ²   con  y¹ y,         x  con  ,         y  con  .

Si può dimostrare (e noi lo abbiamo fatto nel caso della circonferenza) che se il punto P Γ la sua polare coincide con la tangente a Γ in P.

Vale inoltre il seguente teorema la cui dimostrazione esula dai limiti di questo corso:

Teorema della reciprocità: Se la polare di un punto P passa per un punto A, allora la polare del punto  A passa per il punto P.

Alla luce di questo teorema e di quanto abbiamo prima detto possiamo affermare che la retta congiungente i punti A e B di contatto della circonferenza C con le tangenti condotte ad essa da un punto esterno P altro non è che la polare di P e pertanto la sua equazione si ottiene come specificato precedentemente (regola dello sdoppiamento).

 

Nota: che la polare di P sia la retta congiungente i punti di contatto A e B delle tangenti condotte da P alla circonferenza C è ovvio poiché, dette t ¹ e t ² le tangenti condotte da P alla circonferenza C e detti A e B i punti di contatto della circonferenza C con le tangenti t¹ e t ² rispettivamente, la tangente t ¹ per quanto prima affermato altro non è che la polare del punto A, così come la tangente t ² altro non è che la polare del punto B; poiché tali tangenti (polari) passano per P, la polare di P, per il teorema della reciprocità, deve passare per i punti A e B.

 

 

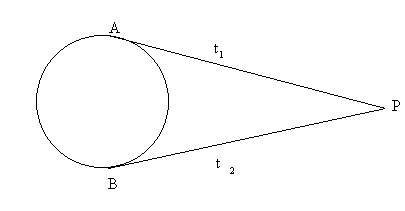
In breve: t ¹ , polare di A, passa per P quindi la polare di P (per il teorema di reciprocità) passa per A; t ² , polare di B passa per P quindi la polare di P (per il teorema di reciprocità) passa per B; pertanto la polare di P passa per A e B.

 

PROF. MICHELE FARINA

 

Torna all'inizio                           Torna al Sommario