ISOMETRIE NEL PIANO

 

Definizione: Si chiama isomeria (o congruenza o movimento rigido) piana ogni similitudine di rapporto 1.

Ponendo nelle equazioni (1) e (2) delle similitudini k=1 si hanno le isometrie, rispettivamente, dirette e inverse.

Per k=1 le (1) diventano:

(7) 

che sono le equazioni delle isometrie dirette o rototraslazioni.

Per α=0 si ha la traslazione:

(8)  .

Per p=q=0 si ha la rotazione:

(9) 

con il centro nell’origine delle coordinate e ampiezza α.

Per α=π , dalle (9) si hanno le equazioni della simmetria centrale di centro O:

(10)  .

Per k=1 le (2) diventano:

(11) 

che sono le equazioni delle isometrie inverse.

Per p=q=α=0 le (11) ci danno:

(12) 

che sono le equazioni della simmetria assiale di asse x.

Per p=q=0 e α=π le (11) ci danno invece:

(13) 

che sono le equazioni della simmetria assiale di asse y.

Osservazione: Per quanto detto risulta chiaro che le equazioni:

(14) 

individuano un’isometria sse

(15) 

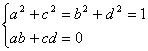
e che :

·        se =1, l’isometria è diretta;

·        se invece = -1, l’isometria è inversa.

PROF. MICHELE FARINA

 

Torna all'inizio                           Torna al Sommario