|
|
La frazione è un operatore che opera su una qualsiasi grandezza e che da come risultato una grandezza omogenea a quella data.
Esempio:
(Il segmento AB è stato
diviso i tre parti e
sono state prese due)
Una frazione è scritta nella
forma:
, dove n è il numeratore, d il denominatore, ed
entrambi sono divisi da una linea detta linea di frazione.
Una frazione divide una grandezza in tante parti quanto è indicato dal denominatore e ne prende tanto quanto è indicato dal numeratore.
Due frazioni sono equivalenti quando applicate alla stessa grandezza danno lo stesso risultato.
Esempio:
quindi
Una frazione può essere trasformata in un’altra equivalente moltiplicando o dividendo il numeratore e il denominatore per uno stesso numero diverso da zero. Questa proprietà è detta proprietà invariantiva delle frazioni.
Per semplificare una frazione si dividono il numeratore e il denominatore per lo stesso fattore.
Esempio:
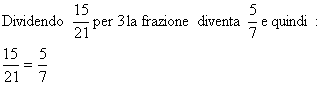
Una frazione si dice ridotta ai minimi termini quando il numeratore e il denominatore sono primi tra loro.
Esempio:
Una frazione per essere ridotta ai minimi termini deve essere semplificata per il M.C.D. tra il numeratore e il denominatore.
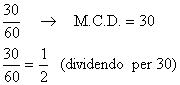
Un numero razionale assoluto è l’insieme di tutte le frazioni equivalenti a una data che viene scelta come rappresentante della classe. Il rappresentante è una frazione ridotta ai minimi termini.
Esempio:
Ci sono tre tipi di frazioni:
-
Frazioni proprie: il numeratore è maggiore del denominatore
(Es: 
)
-
Frazioni improprie: il numeratore è minore del denominatore
(Es: 
)
-
Frazioni apparenti: il numeratore è multiplo del denominatore
(Es: 
TRASFORMAZIONE DI PIU' FRAZIONI IN FRAZIONI EQUIVALENTI AVENTI LO STESSO DENOMINATORE
Per trasformare due o più frazioni in frazioni equivalenti con lo stesso denominatore, si deve scegliere come denominatore comune il m.c.m. tra i denominatori delle frazioni. Si deve poi dividere il nuovo denominatore per il vecchio denominatore e moltiplicare il risultato ottenuto per il vecchio numeratore, ottenendo così il nuovo numeratore.
Esempio:
La trasformazione serve per le operazioni e per il confronto di frazioni.
Es. di confronto:
Consideriamo le frazioni
1) Addizione di frazioni
con stesso denominatore:
Si sommano i numeratori e si conservano i denominatori
Esempio:
2) Addizione di frazioni
con denominatori diversi:
Si applica la trasformazione di più frazioni in frazioni equivalenti con lo stesso denominatore e poi si somma come nel caso 1.
Esempio:
3) Addizione di un numero
intero con una frazione:
Si deve moltiplicare il numero intero per il denominatore della frazione; poi bisogna sommare il risulato ottenuto con numeratore nella frazione, ottenendo così il nuovo numeratore; il nuovo denominatore sarà invece quello della frazione.
Esempio:
1) Sottrazione di frazioni
con stesso denominatore:
Si sottraggono i numeratori e si conservano i denominatori
Esempio:
2) Sottrazione di frazioni
con denominatori diversi:
Si applica la trasformazione di più frazioni in frazioni equivalenti con lo stesso denominatore e poi si sottrae come nel caso 1.
Esempio:
3) Sottrazione di un numero
intero con una frazione:
Si deve moltiplicare il numero intero per il denominatore della frazione; poi bisogna sottrarre al risulato ottenuto il numeratore nella frazione, ottenendo così il nuovo numeratore; il nuovo denominatore sarà invece quello della frazione.
Esempio:
Per moltiplicare due o più frazioni si moltiplicano tra loro i numeratori e i denominatori.
Esempio:
Se è possibile, si possono semplificare le frazioni a croce prima di eseguire la moltiplicazione.
Esempio:
semplifichiamo 3 con 6 e 10 con 15, ottenendo così:
Per dividere due frazioni, si moltiplica la prima per l’inversa della seconda.
Esempio:
dopo aver invertito, si può semplificare come nella moltiplicazione ottenendo:
E’ buona norma tener presenti le seguenti note:
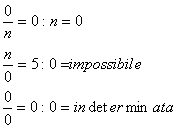
Torna all'inizio Torna al Sommario