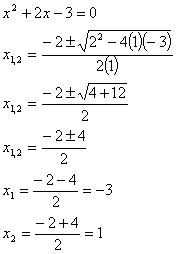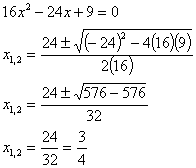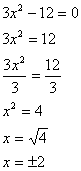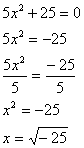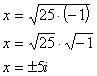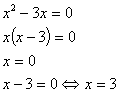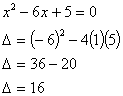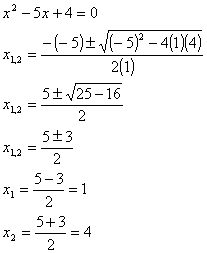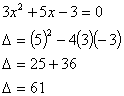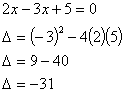 |
Equazioni
di 2° grado
Tipi
di equazioni:
Un’equazione (ad una incognita)
è di 2° grado se può essere scritta nella forma generale (o forma tipica
o ancora forma canonica):
con a, b e c numeri reali (però
a¹0)
oppure espressioni letterali che rappresentano numeri noti ( in tal caso l’equazione
è detta letterale o parametrica). Un’equazione di 2° grado ridotta alla forma
canonica si dice:
1)
completa
quando i tre coefficienti a, b, e c sono tutti diversi da zero ( 
);
2)
pura
quando b vale zero ( 
);
3)
spuria
quando
c vale zero ( 
).
1)
Completa:
Si
risolve adoperando la seguente formula risolutiva:
(formula
normale)
Se
la b è pari si può usare la seguente formula risolutiva:
(formula ridotta)
|
Esempio 1:
|
Esempio 2: |
2)
Pura:
Si
risolve portando al primo membro il termine con la x e al secondo il
termine noto. Dopo si trova la radice quadrata del termine noto.
|
Esempio 1: |
Esempio 2: Se si ottiene la radice di un
numero negativo, che risulterà essere un numero immaginario: essendo i l’unità immaginaria,
ovvero la radice quadrata di –1 |
3)
Spuria:
Si
risolve raccogliendo tutta l’equazione e poi procedendo secondo la legge di
annullamento del prodotto, per la quale un prodotto è uguale a zero se almeno
un fattore è zero. Quindi una soluzione sarà sempre zero.
|
Esempio 1: |
Esempio 2: |
Le soluzioni di un’equazione di 2° grado:
La
formula risolutiva di un’equazione di secondo grado si può anche scrivere:
, dove 
.
Il
D (discriminante) serve a stabilire il tipo di soluzioni
dell’equazione:
Se 
allora le soluzioni sono reali
e distinte;
Se 
allora le soluzioni sono reali
e coincidenti ( 
);
Se 
allora le soluzioni sono complesse
coniugate ( 
).
|
Esempio 1: Quindi le soluzioni sono reali
e distinte |
Esempio 2: Quindi le soluzioni sono complesse
coniugate. |
Somma e prodotto delle soluzioni
e
La
somma e il prodotto delle soluzioni si possono trovare anche con le seguenti
formule:
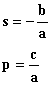
Inoltre
sapendo la somma e il prodotto delle soluzioni si può ricavare l’equazione da
cui derivano con la seguente formula:
Da
tutto ciò si può dedurre che:
-si
può calcolare il valore di due numeri, nota la loro somma e il loro prodotto
|
Esempio: Dato:
si ottiene: |
|
-sapendo
le soluzioni di un’equazione si può ricavare l’equazione da cui derivano:
|
Esempio: Dato: |
|
Si
ottiene:
Scomposizione di un trinomi di secondo grado
(forma canonica dell’equazione di 2° grado)
essendo x 
e x 
soluzioni dell’equazione 
.
|
Esempio: Dato il trinomio |
|
Risolvendo
l’equazione associata, si ottiene:
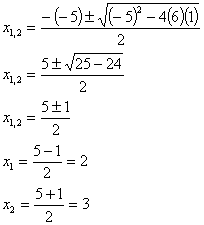
Pertanto:
Regola di Cartesio
La
regola di Cartesio serve a determinare i segni delle soluzioni di un’equazione.
Si può applicare solo se le soluzioni sono reali, ovvero quando 
.
Per
determinare i segni delle soluzioni si esaminano i segni dei coefficienti dell’equazione
(scritta in forma canonica) seguendo il seguente criterio:
Variazione
di segno: radice positiva
Permanenza di segno: radice negativa
|
Esempio 1: Si può applicare la Regola di Cartesio. Esaminiamo i segni: + + - ovvero 1 permanenza, 1 variazione |
Esempio 2: La regola di Cartesio non può
essere applicata. |
Le equazioni di secondo grado fratte
Si
segue il normale criterio, ricordando però di mettere le condizioni di accettabilità.
Esempio:
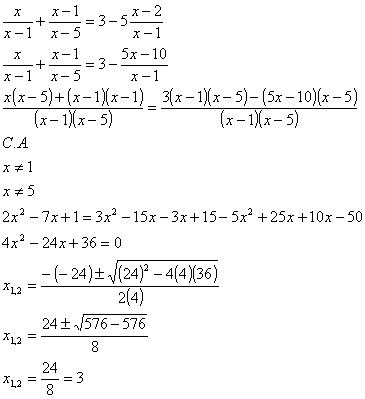
Esempio
di riepilogo
Data la seguente equazione:
a) trovare la forma canonica:
b) determinare i segni delle soluzioni dell’equazione (regola di Cartesio):
Quindi si può applicare la regola di Cartesio.
Esaminiamo i segni: + - + ovvero 2 variazioni
Quindi le soluzioni saranno entrambe positive.
c) trovare le soluzioni dell’equazione:
d) trovare la somma e il prodotto delle soluzioni:
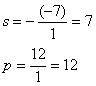
e) scomporre l’equazione:
Equazioni
di secondo grado parametriche
Si dicono equazioni parametriche le equazioni che contengono una o più lettere dette parametri. Queste equazioni danno risultati che variano a seconda del valore attribuito al/ai parametro/i. Quindi non essendoci soluzioni definite, si applica una discussione che ha inizio dopo aver portato l’equazione alla forma canonica.
Esempio per portare un equazione di secondo grado parametrica alla forma canonica:
In
questo caso a, b, c della forma canonica 
saranno:
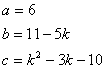
Una volta trovata la forma canonica ha inizio la discussione che varia a seconda delle richieste dell’esercizio da svolgere. Si possono trovare però dei punti generali:
 |
Se l’esercizio chiede di trovare il valore di x in funzione di un k determinato, bisogna sostituire il valore assegnato a k nella forma canonica. |
Esempio:
|
Se l’esercizio chiede di trovare il valore di k in funzione di un x determinato, bisogna sostituire il valore assegnato a x nella forma canonica. |
Esempio:
|
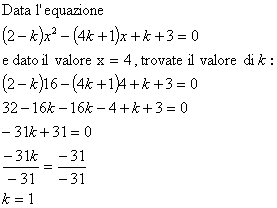
Se l’esercizio
chiede di trovare il valore di k affinché le soluzioni siano
opposte ovvero 
, quindi 
, cioè la loro somma è zero, poiché la Somma è 
, possiamo dire che 
, bisogna quindi trovare quando la somma nell’equazione assegnata è uguale
a zero e il risultato ottenuto sarà il valore di k che l’esercizio
chiedeva. |
Esempio:
|
Se l’esercizio
chiede di trovare il valore di k affinché risulti 
, poiché la Somma è 
, possiamo dire che 
, bisogna quindi imporre che la somma nell’equazione assegnata sia uguale
a n e il risultato ottenuto sarà il valore di k che l’esercizio
chiedeva. |
Esempio:
|
Se l’esercizio
chiede di trovare il valore di k affinché le soluzioni siano
una l’inversa dell’altra, ovvero 
, quindi 
( prodotto delle soluzioni
uguale ad uno), poiché il Prodotto è 
, possiamo dire che 
. Bisogna quindi trovare quando il prodotto nell’equazione assegnata è
uguale a uno e il risultato ottenuto sarà il valore di k che l’esercizio
chiedeva. |
Esempio:
|
Se l’esercizio
chiede di trovare il valore di k affinché risulti 
, poiché il Prodotto è 
, possiamo dire che 
, bisogna quindi trovare per quale valore del parametro k il prodotto
nell’equazione assegnata è uguale a n e il risultato ottenuto sarà
il valore di k che l’esercizio chiedeva. |
Esempio:
|
Se l’esercizio
chiede di trovare i valori da attribuire a
k affinché le soluzioni
siano reali, bisogna trovare i valori di
k per i quali
. |
Esempio:
|
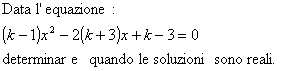
Se l’esercizio
chiede di trovare i valori da attribuire a
k affinché le soluzioni
siano uguali bisogna trovare i valori che k assume quando
. |
Esempio:
|
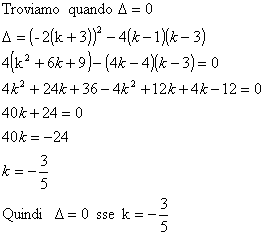
Se l’esercizio chiede di trovare i segni delle soluzioni dell’equazione, bisogna procedere secondo la regola di Cartesio. Poiché i valori di a, b, c variano a seconda del valore di k e di conseguenza anche i loro segni e il discriminante, bisogna fare uno schema per determinarli. Innanzitutto bisogna vedere quando il discriminante (D) è maggiore o uguale a zero (per sapere quando può essere applicata la regola di Cartesio) e quando a, b, c sono maggiori di zero (per sapere quando sono positivi e quando negativi). |
Esempio:
Trovati i valori che servono, si può disegnare uno schema riepilogativo. Le linee orizzontali indicano il segno che D, a, b, c assumono a seconda dei valori di k, mentre le linee verticali servono a individuare gli intervalli, che sono determinati dai risultati ottenuti con le disequazioni sopra fatte. Le linee orizzontali sono continue quando D, a, b, c sono positivi, mentre sono tratteggiate (o, come nell’esempio, non disegnate) quando D, a, b, c sono negativi.
Schema dell’esempio:
-3 -3/5 +1 +3
|
( |
- |
+ |
+ |
+ |
|
( |
- |
- |
+ |
+ |
|
( |
- |
- |
- |
- |
|
( |
- |
- |
- |
+ |
)
)
)
)
Per determinare i segni si va da sinistra verso destra, (e, ma questo non necessariamente, da sopra verso sotto).
|
Se |
|
Se |
|
Se |
|
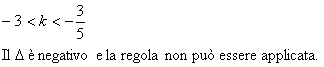
Se |
|
Se |
|
Se |
|
Se |
|
Se |
|
Se |
Torna all'inizio Torna al Sommario