 |
Una trasformazione geometrica è una funzione che fa corrispondere ai punti del piano altri punti del piano stesso (trasformazione biettiva)

Un’isometria è una trasformazione geometrica che lascia invariate le distanze.
Si ha un punto unito in una trasformazione se esso coincide con la sua immagine (trasformato);sono uniti tutti i punti che si trovano sull’asse di simmetria.
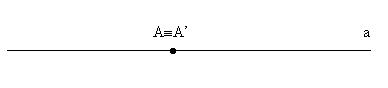
Una retta si chiama unita se i trasformati dei suoi punti appartengono alla stessa retta.

Una retta si dice puntualmente unita se è formata da punti uniti;sono puntualmente unite tutte le rette che sono sovrapposte all’asse di simmetria.
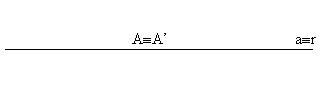
EQUAZIONI DELLE SIMMETRIE ASSIALI
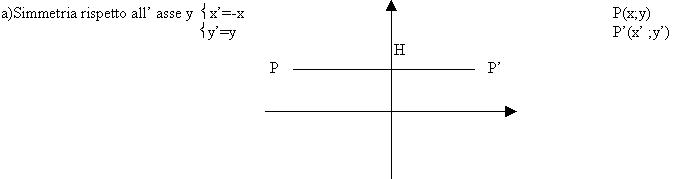
L’ascissa cambia di segno poichè come possiamo osservare dal disegno H sarà il punto medio di PP’ e quindi abbiamo che la distanza PH=P’H e quindi l’ascissa cambia di segno mentre l’ordinata rimane uguale poiché i punti si trovano sulla stessa retta y=K.
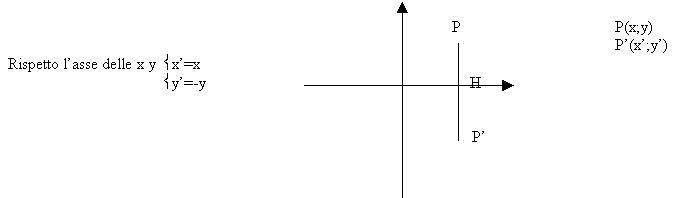
In questo caso accade la stessa cosa della precedente dimostrazione solo che è rispetto all’asse delle x quindi è l’ascissa che rimane invariate poiché si trovano su di una stessa retta x=K mentre l’ordinata cambia di segno.
b)Simmetria rispetto ad una retta parallela all’asse y
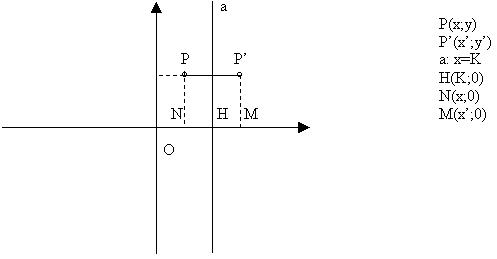
NH=HM Prendendo in considerazione il disegno abbiamo che essendo una isometria,rispetto a r,NH deve esse uguale a HM.
HN=OH-ON
Che tradotto in
coordinate:
HN=K-x
HM=OM-OH
Che tradotto in
coordinate:
HM=x’-K
Quindi eguagliamo le due distanze
K-x=x’-K
x’=2k-x E quindi:
íx¹=2k-x
íy¹=y
Stesso procedimento per una simmetria rispetto ad un asse parallelo all’asse x,però abbiamo: íx¹=x
íy¹=2k-y
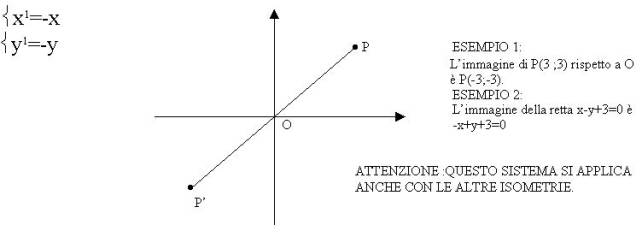
c)Simmetria centrale rispetto a un punto e all’origine degli assi:
Due punti si dicono simmetrici rispetto a C se C rappresenta il punto medio del segmento PP’.
Sono globalmente unite tutte le rette che passano per C.
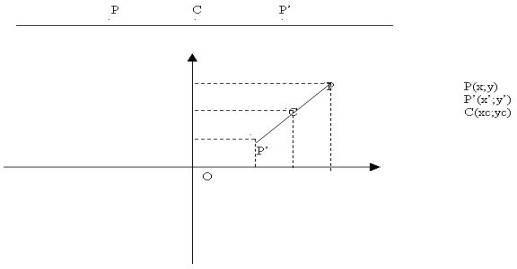
C deve essere considerato come punto medio,quindi C avrà per coordinate C([x+x’]/2;[y+y’]/2);quindi eguagliamo le coordinate di c xc e yc con la formula per calcolarle e visto che in una simmetria centrale dobbiamo calcolare le coordinate dell’immagine di P ossia P’ calcoliamo x’ e y’.
xc=(x+x’)/2
yc=(y+y’)/2
2xc=x+x’
2yc=y+y’
x’=2xc-x
y’=2yc-y
Quindi abbiamo che íx¹=2xc-x
íy¹=2yc-y
Se abbiamo una simmetria centrale rispetto all’origine degli assi O(0;0) basta sostituire a xc e yc le sue coordinate poiché O è il centro di simmetria;e si ha: