 |
DESCRIZIONE GENERALE
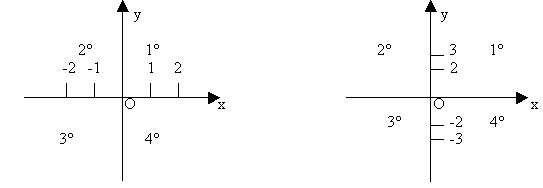
Nella GEOMETRIA ANALITICA si fa sempre un riferimento rispetto al piano cartesiano Oxy; questa riguarda lo studio della retta, delle trasformazioni lineari piane e delle coniche. E’ importante sapere che nella Geometria Analitica ad ogni equazione corrisponde un particolare luogo geometrico. Un piano cartesiano è formato da due rette orientate e perpendicolari. La retta orizzontale e detta asse delle X o ascissa, la verticale è detta asse delle y o ordinata; il loro incontro si indica con O (origine) che ha coordinate O(0; 0); ad ogni punto su di un piano cartesiano viene associata un’ascissa e un’ordinata P(x; y) , x è l’ascissa del punto P e y l’ordinata. Sull’asse delle x verso destra da O troviamo i numeri positivi, verso sinistra i negativi; sull’asse delle y verso l’altro rispetto a O troviamo i positivi, verso il basso i negativi. Il piano cartesiano si divide in quattro quadranti:
1) Il primo ha ascissa e ordinata positiva;
2) Il secondo ha ascissa negativa e ordinata positiva;
3) Il terzo ha ascissa negativa e ordinata negativa;
4) Il quarto ha ascissa positiva e ordinata negativa.
1) RETTA
L’equazione di una retta è una semplice equazione di 1° grado a due incognite:
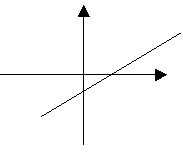
a) se l’equazione è y=mx (dove m è un coefficiente della x) abbiamo che la retta passa per l’origine;
b) se l’equazione si presente y=mx+q (dove q è un qualsiasi numero reale) si ha una retta generica del piano.
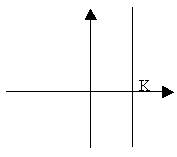
Questa potrà anche avere una sola incognita ma in questo caso sarà parallela all’asse x o all’asse y:
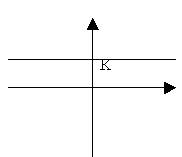
a) se l’equazione si presenta in questo modo x=K (dove K è un qualsiasi numero) la retta sarà parallela all’asse delle y;
b) se l’equazione sarà y=K la retta sarà parallela all’asse delle x.
La distanza tra due punti è data dalla radice della somma del quadrato della differenza tra le coordinate omonime,
_______________
d=\/(x1-x2)
²+(y1+y2) ²
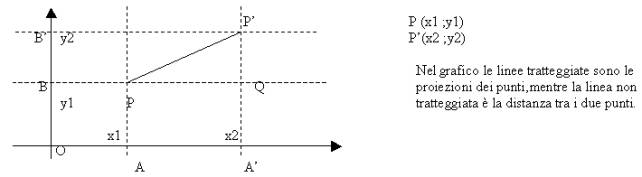OA=x1
OA’=x2 Poiché AA’ sarà uguale a PQ e BB’ sarà uguale a P’Q, calcolando la loro
BO=y1 distanza, possiamo applicare il teorema di Pitagora per calcolare la distanza
B’O=y2
PP’.
BB’≡P’Q
AA’≡PQ
BB’=B’O-BO=y2-y1
AA’=A’O-AO=x2-x1
d²=(x2-x1)
²+(y2-y1) ²
______________
d=\/(x2-x1)
²+(y2-y1) ²
ATTENZIONE : QUESTO PASSAGGIO PUO’ ESSERE SEMPLIFICATO QUANDO I PUNTI HANNO LA STESSA ASCISSA E ORDINATA E SE HANNO LA STESSA ASCISSA SI FA IL VALORE ASSOLUTO DELLA DIFFERENZA DELLE ORDINATE LA MAGGIORE MENO LA MINORE; SE HANNO LA STESSA ORDINATA SI FA IL VALORE ASSOLUTO DELLA DIFFERENZA TRA LE ASCISSE LA MAGGIORE MENO LA MINORE.
Le coordinate del punto medio tra due punti sono date dalla media aritmetica tra le coordinate omonime degli estremi.
M([x1+x2]/2;
[y1+y2]/2)
L’equazione canonica della retta è ax+by+c=0.
La forma implicita è ax+by+c=0, mentre quella esplicita è y=-(ax+c)/b. +
Il coefficiente angolare m indica la pendenza della retta rispetto all’asse x; m è dato dal coefficiente della x.
Per determinare se due rette sono parallele basta guardare i loro coefficienti angolari indicati con m:
a) se i due coefficienti angolari m e m’ sono uguali si avrà che le rette saranno parallele;
b) se i due coefficienti angolari sono uno l’antireciproco dell’altro (m=-1/m’) le rette saranno perpendicolari;
c) se i coefficienti non sono uguali o sono antireciproci, le rette saranno solo incidenti.
Se un punto si trova su di una retta, le sue coordinate verificano l’equazione
Es: y=5x+3 P(1; 8) sostituendo verrà 8=5+3 ; 8=8
Si verifica che un punto P sta su di una retta sostituendo alla y e alla x della retta rispettivamente la y e la x di P.
Per sostituire viene usato il metodo della croce, prendendo in riferimento l’esempio precedente:
x
y
Quindi facendo così, sappiamo che sostituendo alla x il valore –1
abbiamo che la y sarà –2 quindi
1 8 i punti saranno infiniti poiché ad ogni x corrisponde una y, e viceversa.
-1 -2
DIMOSTRAZIONI
Quando due rette sono parallele:
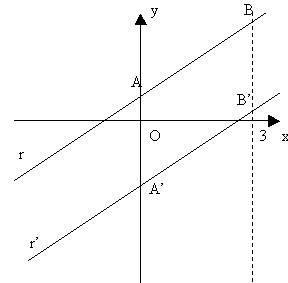
r: y=mx+q
r’:
y=m’x+q’
Hp:
r//r’
Th :
m=m’
A (0 ; q)
A’(0 ; q’) Poniamo i punti A e A’ di coordinate A(0 ; q) e il punto A’(0; q’), questi avranno queste coordinate poiché i punti si troveranno sull’asse delle y e quindi sostituendo nell’equazione di r , x=0 si avrà y=q, il concetto vale per entrambi i punti.
x=3 Prendiamo una qualsiasi retta perpendicolare all’asse delle x.
Procedendo come prima con A e A’ ci ricaviamo le coordinate dei punti B e
B (3; 3m+q) B’. Quindi abbiamo che AA’BB’ sarà un parallelogramma, poiché è formato
B’(3 ; 3m’+q’) da due coppie di rette parallele.
__ __
AA’=BB’ Poiché i lati opposti del parallelogramma sono uguali.
__
AA’=|q-q’|
__
BB’=|3m+q-3m’-q’|
Quindi abbiamo che:
q-q’=3m+q-3m’-q’ semplificando si ha:
3m=3m’
m=m’
Quando due rette sono perpendicolari:
A(2; 2m)
B(2; 2m’)
Le distanze si calcolano normalmente e si ha che:
AH=2m
HB=-2m’
OH=2
AH:OH=OH:HB Poiché si avrà un triangolo rettangolo, possiamo applicare il teorema di Euclide
OH²=AH*HB Sostituendo:
4=2m(-2m’)
4=-4mm’
-1=mm’
Molto importante nello studio della retta è il fascio proprio e improprio. Il fascio proprio genera retta di tutti i tipi dalle parallele alle perpendicolari o altre solo incidenti; il fascio improprio genera rette parallele, e per questo è chiamato improprio perché si crede che due rette parallele si incontrano in un punto immaginario detto improprio.
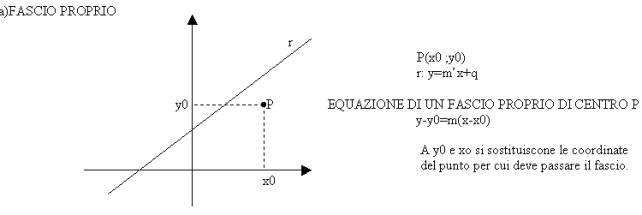Se
si vuole una retta parallela si mette al posto di m del fascio la stessa
m’di r; se si vuole una retta perpendicolare si mette al posto di m
l’antireciproca di m’.
ESEMPIO:
Vogliamo trovare la retta parallela e perpendicolare alla retta y=(4x-3) /3 passante per P(3;2).
Parallela
m=4/3
y-y0=m(x-x0)
y-2=4(x-3)
/3
y=4x/3-2
Perpendicolare
m’=4/3
m=-3/4
y-y0=m(x-x0)
y-2=-3(x-3)
/4
y=-(3x+17)
/4
FASCIO IMPROPRIO
L’equazione di un fascio improprio è y=mx+q dove m e costante e q varia. Infatti come già dimostrato due rette che hanno lo stesso coefficiente angolare sono parallele.
ESEMPIO:
Trovare una qualsiasi retta parallela a y=8x+76.
y=mx+q
poiché
m=8
y=8x+q
e quindi le rette saranno parallele per qualsiasi valore di q
Es:
y=8x-5
y=8x [+0]