Appunti di Cartografia
1) Cenni storici
La terra è antica quanto la scienza cartografica, si pensa che un abitante dell’Asia Minore di nome Aristagora intorno al 500 a.c. abbia presentato agli Spartani una carta geografica disegnata su tavolette di bronzo e con esse li abbia incitati alla guerra contro la Persia di Dario I. Della Cartografia furoni fondatori Eratostene, che misurò per primo il raggio terrestre ed un arco di meridiano ed il messinese Dicearco 300 a.c. , quest'ultimo tentò di misurare le dimensioni della Terra forse prima di Eratostene ( nel numero di Febbraio 1998 del National Geographic Magazine pagg. 8 e 9 c'è una foto del pozzo di Assuan dove Eratostene si pensa che provò le sue tesi durante il solstizio d'estate ).Dicearco divise lo spazio conosciuto con una sorta di reticolato anticipando i meridiani ed i paralleli; la parola meridiano deriva dal latino " meridies " , due punti che hanno la stessa ora a mezzogiorno si trovano sullo stesso meridiano. Ipparco (190 - 125 a.c.) che fù sicuramente il più grande astronomo dell'età greca , criticò la carta di Eratostene a causa della mancanza di riferimenti precisi e determinò la posizione di numerose località con misurazioni di longitudine ottenute dopo ripetute osservazioni astronomiche. L'inizio delle conquiste romane ed il rilievo dei territori occupati a scopo fiscale portò alle grandi opere cartografiche iniziate da Cesare e concluse da Augusto ( 44 - 19 a.c. ). Marino di Tiro ( 110 d.c. ) sulle basi del lavoro di Ipparco introdusse per primo la misura della longitudine e della latitudine in gradi d'arco anziche in stadi.Tolomeo, vissuto fra il 90 d.c. e il 170 d.c. ,condizionato dall' opera di Marino di Tiro, inventò le prime Proiezioni Cartografiche ; egli introdusse due proiezioni che sebbene come coniche non furono considerate tali. Nel Medioevo la Cartografia fu tutta a base di stime, lo studio e la ricerca furono seppelliti all'interno dei monasteri , dove solo pochi monaci potevano avere accesso. In questo periodo sono gli arabi a custodire la tradizione Tolemaica studiandola e riconsegnandola all' Occidente come inizio di un nuovo periodo di rinascita Cartografica. Nel XIII secolo con lo svilupparsi dell'uso della bussola nasce una cartografia nuova, quella nautica , che usa i portolani, carte costruite in base ad osservazioni di angoli e distanze, carte che assumevano un valore inestimabile. Nel XV e nel XVI secolo, anche con l'avvento della stampa e delle imprese marinare, ci fù una rivoluzione cartografica dovuta all' enorme diffusione delle carte. L'abbandono del Mediterraneo, le straordinarie imprese oceaniche, il bisogno di conoscere la posizione in mare, portò alla costruzione dei primi strumenti geodetici. Da questo momento in poi vengono sviluppate le Proiezioni utilizzate ancora oggi e che vedremo di seguito esposte con una traccia dei loro autori più famosi.
Fig. B
2) La forma della Terra
I primi essere umani credevano che la terra attorno a loro fosse piatta ( c'è qualcuno che ancora oggi crede che la Terra non abbia una forma pressochè sferica ). L'idea della sfericità venne ai filosofi dell'era pre-Cristiana che si posero a ragionare su questo problema; 500 anni o più prima della nascita di Cristo si formò la teoria della Terra sferica. La sfericità della Terra fu generalmente riconosciuta dal secondo secolo A.D. Se noi togliamo le irregolarità della crosta terrestre, la forma della Terra si può approssimare ad una sfera. La forma assunta dal nostro pianeta, che ruota attorno al suo asse polare nello spazio, è il risultato dell' interazione della forza centrifuga di rotazione, della forza di attrazione gravitazionale newtoniana e delle variazioni di densità delle rocce che la costituiscono. La tettonica a zolle ha prodotto irregolarità della crosta terrestre molto lievi rispetto al raggio equatoriale; basti pensare che su un mappamondo del raggio di 25 cm. il monte Everest sarebbe alto appena 0.032 cm.
3) Il geoide
Il geoide è la forma che assumerebbe il livello del mare indisturbato attraversante i continenti. Il geoide è una superficie equipotenziale in cui il piano tangente in ogni punto è perpendicolare alla direzione del filo a piombo in quel punto cioè alla verticale passante per quel punto. Questa superficie è influenzata dalle variazioni di densità della Terra e generalmente si alza sopra i continenti per abbassarsi sugli oceani. Le irregolarità del geoide sono pari a circa 60 m. La geodesia ha una parte fondamentale nella determinazione della forma precisa della Terra.
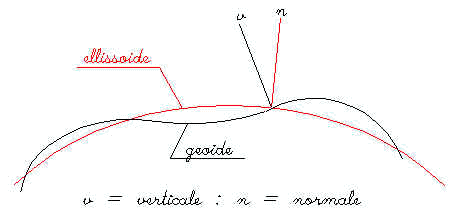Fig. 1
4) L' ellissoide
L' ellissoide è la forma geometrica della Terra. La Terra è schiacciata ai poli. La differenza fra il raggio equatoriale e polare è pari a circa 21.5 km. e dipende dall' ellissoide che viene considerato. Il Programma Atlas.exe scaricabile dal sito utilizza l'ellissoide di Clarke 1866 avente i seguenti parametri:
a= Raggio equatoriale = 6378206 m. b= Raggio polare = 6356584 m. 1/f = 294.98
Se si considera la sfera di eguale area -----> RSphere = 6370997 m.
L'ellissoide è una superficie ottenuta facendo ruotare un ellisse attorno al suo asse minore.
f= (a-b)/a
Nella figura sottostante si è fatta coincidere la verticale
v con la normale n , in realtà se si considera l'ellissoide si dovrebbe considerare la normale, se si considera il geoide la verticale.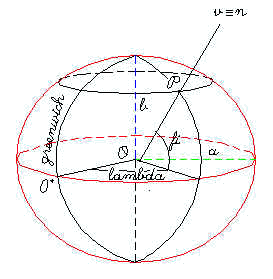
Fig. 2
5) Le Proiezioni Cartografiche
La sola vera rappresentazione della Terra libera da distorsioni è il globo. Il procedimento mediante il quale si passa dalla superficie sferica della Terra ad una superficie bidimensionale si chiama Proiezione. Questo può essere compiuto tramite proiezione geometrica diretta o tramite l'uso di formule matematiche che modificando le leggi proiettive arrivano a determinate condizioni. Le relazioni che legano un punto sulla carta con un punto sull'ellissoide o sulla sfera equivalente si chiamo Equazioni della Carta ; queste possono essere dirette o inverse. La più corta distanza fra 2 punti è una retta; sulla sfera sarebbe impossibile collegare 2 punti con una retta per avere la minor distanza. Sulla terra la più corta distanza fra 2 punti è l'arco che unisce i 2 punti ottenuto dall'intersezione della sfera con il piano passante per i 2 punti e per il centro della terra ( arco di cerchio massimo ). Questa linea si chiama Ortodromica e taglia i meridiani sotto angoli sempre diversi. Qualsiasi cerchio massimo taglia la Terra in maniera che per metà esso si trova in un emisfero e per l'altra metà nell' emisfero opposto. La linea che taglia i meridiani sotto lo stesso angolo si chiama Lossodromica la lunghezza della Lossodromica è superiore alla corrispondente Ortodromica, però ha il vantaggio di essere il percorso più facile da seguire. Tracciando una linea diritta fra due punti su una carta di Mercatore abbiamo la rotta da seguire dopo le opportune correzioni alla declinazione della bussola.
6) I Sistemi di Coordinate
E' necessario posizionare un punto rispetto ad un altro punto per sviluppare il concetto di direzione e distanza. Questo può essere fatto utilizzando diversi sistemi.
Sistema di riferimento per Coordinate Rettangolari Piane
Tutti i punti sono riferiti ad un sistema di assi perpendicolari
fra loro;
Asse Verticale = Asse delle Ordinate ,
Asse Orizzontale = Asse delle Ascisse.
Il punto d'incontro di questi Assi si chiama Origine. La posizione di un punto viene
definita per mezzo delle distanze del punto da questi assi.
Sistema di riferimento per Coordinate Geodetiche Rettangolari
Tutti i punti sono riferiti ad un sistema in cui l'origine è sempre in
O. Questa volta la posizione di un punto P viene definita dall' ascissa , che è la geodetica per P perpendicolare al meridiano passante per O ( P P') e dall' ordinata che è l'arco di meridiano compreso fra O e il punto P' precedentemente descritto.Sistema di riferimento per Coordinate Polari Piane
Tutti i punti sono riferiti ad un sistema costituito da un punto
P che si chiama polo e da un semiasse verticale che si dirige verso l'alto ( generalmente il Nord Magnetico o Geografico ) da P. La posizione di un punto S viene definita per mezzo della distanza del punto dal polo P e dall'angolo ( azimut (PS) ) che l'asse verticale forma ruotando in senso orario fino a sovrapporsi alla direzione PS considerata. S(PS,(PS)).Sistema di riferimento per Coordinate Geodetiche Polari
Tutti i punti sono riferiti ad un sistema costituito da un punto
P che si chiama polo e dal meridiano passante per P. La posizione di un punto S viene definita per mezzo della distanza s = arco di geodetica PS e dall'angolo ( azimut (PS) ) che il meridiano passante per P forma ruotando in senso orario fino a sovrapporsi alla direzione PS considerata. S(PS,(PS))Sistema di riferimento per Coordinate Geografiche Ellissoidiche
La posizione dei punti viene individuata facendo riferimento ad un sistema di linee in cui ne vengono fissate 2 di riferimento. I paralleli sono le linee ottenute mediante l'intersezione di piani paralleli all'equatore con l'ellissoide mentre i meridiani sono le linee di intersezione degli archi di cerchio massimo con l' ellissoide. Le linee di riferimento sono l' equatore ed il meridiano di Greenwich. La posizione di un punto
P viene definita mediante la Longitudine ( angolo diedro che il piano contenente il meridiano di Greenwich forma con il piano contenente il meridiano del punto P ) ( lambda ) e la Latitudine ( angolo che la normale all'ellissoide passante per P forma con il piano equatoriale) ( fi ) Fig.2 . Equatore = Luogo dei punti con Latitudine 0°.0000 : Meridiano = Luogo dei punti con Longitudine costante. I punti situati nell'emisfero boreale hanno Latitudine Nord positiva da 0°.0000 a 90°.0000 ( Polo Nord). I punti situati nell'emisfero australe hanno Latitudine Sud da 0°.0000 a -90°.0000 ( Polo Sud ). I punti situati a Est del meridiano di Greenwich hanno valori di Longitudine da 0°.0000 a 180°.0000 mentre i punti situati a Ovest del meridiano di Greenwich hanno valori di Longitudine da 0°.0000 a -180°.0000.7) Proprietà delle Proiezioni
E' inevitabile che in ogni proiezione ci siano errori di distorsione nel passaggio da una superficie sferica a una piana. Ogni proiezione distorce una,due,tre e a volte tutte le seguenti proprietà. Forma, Area, Distanza e Direzione.
Conforme
Nessuna mappa preserva la forma di grandi aree, ma una proiezione conforme mantiene le forme in piccole e localizzate aree.Questa proiezione è accompagnata dall'esatta trasformazione degli angoli attorno ai punti. Condizione necessaria è che i paralleli e i meridiani si incontrino perpendicolarmente come sul globo. Questa proprietà viene sfruttata nella realizzazione delle carte nautiche. Spesso viene definita true-shape anche se la qualità della forma è limitata.
Equivalente
Mostra le aree di tutte le zone sulla mappa nella scala di rappresentazione.Preservare le aree vuol dire trasformare in maniera inesatta gli angoli attorno ai punti quindi esclusione della proprietà precedentemente descritta. Questa proprietà è molto importante nelle mappe catastali in cui il fisco tassa le proprietà in base alla loro superficie.
Equidistante
Nessuna mappa può rappresentare la corretta distanza fra 2 punti, ma solo da uno o al massimo da 2 punti a ogni altro punto. Di solito l'equidistanza è lungo l'equatore, lungo il meridiano appartenente al centro di proiezione oppure lungo uno o due paralleli standard o meridiani standard.
Azimutale
Mostra la corretta direzione ( azimut ) fra due punti ; la linea che unisce i due punti taglia i meridiani sotto lo stesso angolo " Linea Lossodromica " . Comunque su una superficie sferica la più corta distanza fra due punti è un cerchio massimo lungo il quale gli azimut cambiano costantemente. Tutti i meridiani sono cerchi massimi mentre l'equatore è l'unico parallelo che è un cerchio massimo .
8) Classificazione delle proiezioni
Un metodo di classificare le proiezioni è quello di raggrupparle nel tipo di superficie in cui il reticolo è stato proiettato.
Le principali proiezioni sono:
AzimutaliUn piano è tangente al globo, il punto di contatto è il centro di proiezione. Se una sorgente di luce all’interno del globo proietta la luce sul piano, il risultato sarà una proiezione azimutale. La scelta del Centro di Proiezione determina l'aspetto della proiezione. Nell' Aspetto Polare il centro di proiezione è il polo, nell' Aspetto Equatoriale il centro di proiezione è un punto sull' equatore, nell' Aspetto Obliquo il centro di proiezione è un qualsiasi altro punto.
Le principali proiezioni azimutali sono:
Azimutale Equidistante : E' probabile che questa proiezione sia stata usata per la prima volta dagli Egiziani per la rappresentazione delle mappe stellari. Questa proiezione non è né conforme né equivalente. I paralleli sono generalmente curve complesse , solo nell'aspetto polare sono cerchi. L'equatore è una linea diritta nell'aspetto equatoriale , la maggio parte dei meridiani sono curve complesse , fanno eccezione i meridiani nell'aspetto polare ed il meridiano centrale che sono linee diritte. Le distanze misurate dal centro di proiezione sono vere; le distanze che non sono misurate lungo i raggi dal centro non sono corrette. L'unico punto senza distorsioni è il centro di proiezione. Con questa proiezione può essere rappresentata tutta la Terra. Il polo del centro di proiezione è un punto , mentre l'altro polo è un cerchio con raggio doppio di quello equatoriale.
Proiezione Azimutale Equidistante
Gnomonica: Il punto di vista
V è nel centro del globo O, tutti i meridiani e l’equatore sono linee diritte, tutti i paralleli eccetto, l’equatore ed i poli sono, ellissi, parabole o iperbole. Questa proiezione non è né conforme né equivalente, meno di un emisfero può essere visto. Solo al centro di proiezione C non ci sono distorsioni , le distorsioni aumentano via via che ci si allontana dal centro di proiezione.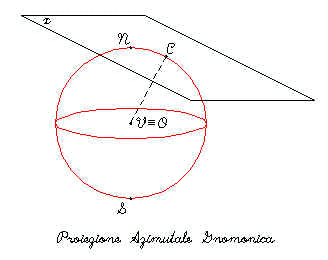
Fig.3
Proiezione Gnomonica Aspetto Equatoriale ed Obliquo
Stereografica:Il punto di vista
V e dalla parte opposta al centro di proiezione C . Viene usata per rappresentare le zone vicino le regioni polari. La proiezione è Conforme. Tutti i meridiani nella visione polare e l’ equatore nella visione equatoriale sono linee rette. Tutti gli altri meridiani e paralleli sono archi di cerchio. Le direzioni dal centro di proiezione sono vere ( eccetto su quella obliqua ellissoidale ed equatoriale ). La scala aumenta via via che ci si allontana dal centro di proiezione.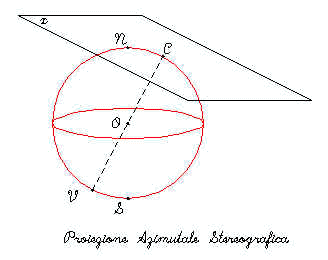
Fig.4
Proiezione Stereografica Aspetto Equatoriale
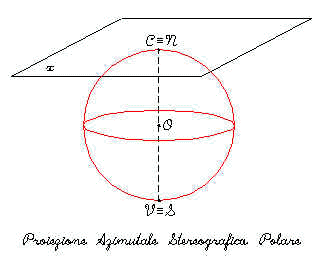Fig.5
Ortografica: Il punto di vista è all’infinito V , è visibile solo un emisfero. La proiezione non è né conforme né equivalente. Le maggiori distorsioni sono ai bordi dell’emisfero. Nessuna distorsione vicino al centro di proiezione C . Le direzioni dal centro sono vere. Il fattore di scala radiale diminuisce all’aumentare della distanza dal centro.
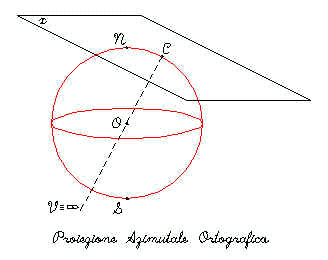Fig.6
Azimutale Equivalente di Lambert: Questa proiezione fù presentata da Johann Heinrich Lambert in 1772. E' anche conosciuta come proiezione Zenitale Equivalente. La proiezione del tipo azimutale non prospettico è equivalente. Solo il centro di proiezione è libero da distorsioni, ma le distorsioni sono moderate in un area di 90° intorno a questo punto. La scala è vera solo nel centro di proiezione, aumenta in maniera tangenziale e diminuisce radialmente dal centro di proiezione. La proiezione non è nè conforme nè equidistante.Con questa proiezione è possibile vedere tutto il globo. Frequentemente usate nella rappresentazione delle regioni polari.
Proiezione Azimutale Equivalente di Lambert Aspetto Obliquo
Johann Heinrich Lambert ( 1728-1777) nacque il 26/08/1728 in Alsazia l'odierna Svizzera. Si fece da solo, visto che abbandonò la scuola all'età di 12 anni per aiutare suo padre che faceva il sarto. Durante questo periodo lesse esclusivamente libri di matematica, astronomia e fisica , ma non ritornò più a scuola. All'età di 20 anni già era padrone di quelle discipline da lui preferite e parlava correntemente 5 lingue (tedesco, francese, italiano, latino, e greco).Nel 1761 egli divenno membro dell'Accademia di Federico il Grande a Berlino. Iniziò a lavorare per lui nel 1764. Dopo un anno Federico lo mise nel Comitato Direttivo dell' Accademia vicino a due famosi matematici come Leonhard Euler e Joseph-Louis Lagrange. Mentre era al servizio di Federico Lambert dimostrò che la costante ¶ era irrazionale e sviluppò la funzione iperbolica in trigonometria. Fù durante questo periodo che creò le Proiezioni Cartografiche la più famosa delle quali ( Lambert Conformal Conic ) fù usata per la rappresentazione della Russia e del Mediterraneo. Johann Heinrich Lambert morì di malattia respiratoria il 25/09/1777. Sebbene molti lo ricordino per le sue Proiezioni fu più che un cartografo visto che dedicò la maggior parte della sua vita allo studio di discipline parallele.
Il reticolo viene proiettato su un cilindro; la proiezione si dice diretta se il cilindro è tangente all’ equatore, si dice inversa se è tangente a un meridiano, si dice secante se è tangente a un parallelo diverso dall’equatore, si dice obliqua se le direttrici del cilindro non sono ortogonali o parallele all’asse polare. Il punto di vista è nel centro del globo. Meridiani e paralleli sono linee diritte. Questa proiezione fa si che le dilatazioni aumentino via via che ci si allontana dall’equatore; proprio per questo la proiezione viene utilizzata per rappresentare le zone intorno all’equatore.
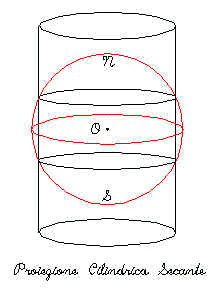Fig.7
Le principali proiezioni cilindriche sono:
Miller: Osborn Maitland MIller presentò questa proiezione nel 1942. Il cilindro è tangente alla sfera lungo l'equatore. Questa proiezione ha meridiani e paralleli diritti, perpendicolari quindi fra loro,ma le linee diritte non hanno azimut costante. La lunghezza dei meridiani è pari a 0.73 volte circa quella dell'equatore. I paralleli sono spaziati diversamente, la distanza fra loro aumenta all' avvicinarsi verso i poli, comunque questa distanza è sempre minore di quella della proiezione diretta di Mercatore; questo fa si che i poli possono essere rappresentati. La proiezione di Miller non è nè equivalente nè equidistante, nè conforme nè prospettica. La scala è vera solo lungo l’equatore. Le distorsioni diventato inaccettabili ai poli. Questa proiezione evita le esagerazioni di scala della proiezione di Mercatore.
Mercatore: Disegnata da Gerardo Mercatore nel 1569,questa proiezione ha meridiani e paralleli diritti, la scala è vera lungo il parallelo di tangenza. Questa proiezione è usata per la navigazione in quanto tutte le linee diritte sulla mappa hanno azimut costante. Per preservare la Conformalità della mappa i paralleli aumentato la distanza dall'equatore. A causa delle grandi deformazioni raramente è estesa oltre 80°.0000 di latitudine Nord o Sud.
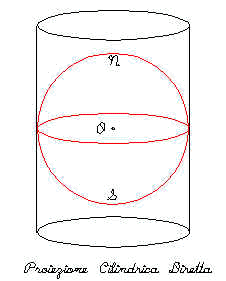Fig.8
Gerardo Mercatore (1512-1594) nacque a Rupelmunde nelle Fiandre ( Belgio ) il 05/03/1512 il suo vero nome era Gerhard de Kramer. Egli dedicò la sua vita alla Cartografia sebbene fù anche scienziato e straordinario incisore. Figlio di un calzolaio frequentò l'Università di Louvain dove studiò filosofia ed umanesimo. Si laureò nel 1532 e subito si imbarcò per cercare le prove della parola della Bibbia in antitesi con le opinioni di Aristotele. Non pervenne a nessuna conclusione, acquistò invece la passione per la Geografia. Nel 1535 aprì un laboratorio di cartografia e nel 1537 realizzò la sua prima mappa , un proiezione equivalente della Palestina. La Proiezione di Mercatore del mondo fu realizzata nel 1538 e fù a quel tempo una grande conquista. Si avvicinò ai problemi legati alla navigazione creando una proiezione dove le linee diritte compensano le variazioni e le deviazioni magnetiche. Queste linee sono conosciute come lossodromiche. Nel 1540 realizzò ed incise una mappa delle Fiandre a cui prestò attenzione il Cardinale di Grandeville ( Primo Ministro di Carlo IV ) che gli commissionò la realizzazione di un mappamondo per l' Imperatore che realizzò nel 1541. Nel 1544 scampò per miracolo dalla morte quando fù imprigionato per 7 mesi con l'accusa di eresia dalla Regina di Ungheria che era contraria alla riforma protestante. La maggior parte degli uomini e delle donne considerati essere eretici luterani furono messi a morte. Mercatore abbandonò le idee religiose appena venne rilasciato. Nel 1552 fù nominato Cosmografo da Carlo V. Negli anni seguenti Mercatore realizzò numerose mappe , molte delle quali non furono mai pubblicate. Nel 1594 morì ad Antwerp una città delle Fiandre. Sebbene molti suoi lavori sono andati dimenticati o perduti, la sua proiezione più famosa è ancora lo standard per la navigazione.
Oblique Mercator Hotine A e B: Proiezione obliqua. E' stata usata all'inizio per cartografare le regioni che avevano uno sviluppo obliquo rispetto ai meridiani e ai paralleli. Fu usata prima della Space Oblique Mercator per mappare i Landsat. La proiezione è conforme. I paralleli sono curve complesse. I meridiani sono curve complesse eccetto i due meridiani che sono ai lati che sono linee diritte. La scala tende all' infinito a 90°.0000 dalla linea centrale. La Hotine A usa 2 punti che appartengono alla linea centrale, il primo punto fissa il punto di contatto mentre il secondo dà la direzione. La Hotine B usa un punto centrale di contatto ed un Azimuth per dare la rotazione al cilindro di tangenza ; Azimuth = 0°.0000 proiezione cilindrica trasversa; Azimuth = 90°.00000 proiezione cilindrica diretta. Le distanze sono vere lungo il cerchio massimo di tangenza.
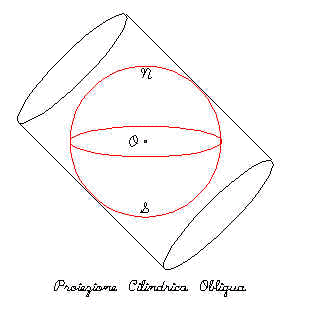Fig.9
Cassini : Questa Proiezione è l'aspetto obliquo della proiezione di Plate Carrée, fù sviluppata da César François Cassini de Thury (1714-84). E' tuttora usata per il rilevamento topografico di alcuni paesi. Il Meridiano centrale è una linea diritta (include il Meridiano opposto al Meridiano Centrale in una linea continua). Gli altri Meridiani sono linee diritte se sono 90º dal Meridiano Centrale altrimenti sono curve complesse concave verso il Meridiano Centrale. I Paralleli sono curve complesse concave verso il polo più vicino. I poli sono punti lungo il meridiano centrale. La simmetria è lungo qualsiasi meridiano diritto o l'Equatore. Questa è una proiezione in un cilindro è tangente al Meridiano Centrale. Le distorsioni sia della forma che dell'area sono in funzione della distanza dal Meridiano Centrale. La scala è vera lungo il Meridiano Centrale e lungo qualsiasi linea diritta perpendicolare al Meridiano Centrale (i.e., è Equidistante). Per proiezioni cilindriche, solamente uno Parallelo Standard viene specificato. L'altro parallelo standard è posto alla stessa latitudine ma con segno opposto. Per questa proiezione, il Parallelo Standard per definizione viene fissato a 0º.
Equirettangolare : Proiezione equivalente. Nella versione classica i meridiani sono linee rette ugualmente spaziate, mentre i paralleli sono linee rette diversamente spaziate più ravvicinate ai poli che tagliano i meridiani con il giusto angolo. La scala è vera lungo l’equatore o lungo 2 paralleli equidistanti dall’equatore. Nella versione trasversa, il meridiano centrale e l’equatore sono linee rette, mentre gli altri paralleli e meridiani sono curve complesse.
U.T.M. : The Universal Trasverse Mercator Projection divide il mondo in zone verticali ampie 6° e fasce orizzontali ampie 8°. La proiezione ha il suo centro nel meridiano centrale della zona considerata. Le zone si estendono da 80° Latitudine Sud a 84° Latitudine Nord. L’ascissa convenzionale del meridiano centrale viene fissata generalmente in 500 km ,per l’emisfero Nord l’ordinata viene fissata a 0.00 km mentre per l’emisfero Sud l’ordinata viene fissata a 10000 km
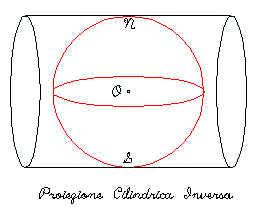Fig.10
La proiezione PseudoCilindrica richiama le Proiezioni Cilindriche ma in questo caso mentre i paralleli sono diritti i meridiani sono curvi.
Le principali proiezioni pseudocilindriche sono:
Robinson: Questa proiezione fù presentata da Arthur H. Robinson nel 1963 è anche chiamata The Orthophanic projection, che significa right appearing. Il meridiano centrale è una linea diritta lunga 0.51 volte l'equatore, mentre gli altri meridiani assomigliano ad archi ellittici concavi verso il meridiano centrale. I paralleli sono linee diritte perpendicolari al meridiano centrale; sono spaziati egualmente fino a 38° di latitudine, oltre questo limite le distanze decrescono. I poli sono linee lunghe 0.53 volte l' equatore. La scala è vera solo lungo il 38° parallelo ed è costante lungo qualsiasi parallelo o tra ogni coppia di paralleli equidistanti dall' equatore. Le distorsioni sono limitate entro 45° dal centro e lungo l'equatore. Questa proiezione non è equivalente, nè conforme , nè equidistante, è quindi una proiezione che tende ad avere deformazioni contenute. E' da considerare comunque una buona proiezione per la rappresentazione del mondo. Fù la Rand McNally Publishing Company che commissionò a Robinson la sua realizzazione. E' sicuramente la migliore proiezione per la rappresentazione del mondo come dimensione e forma. Nel 1988 the National Geographic Society sostituì la proiezione con cui aveva rappresentato il mondo per 65 anni con la Proiezione di Robinson. La caratteristica di questa proiezione è l'uso di tabelle di coordinate anzichè formule matematiche di proiezione del reticolo.
Fig. E
Mollweide: Questa proiezione equivalente ( presentata da Karl Mollweide nel 1805 ) è utilizzata per la rappresentazione del mondo. Il meridiano centrale è diritto e perpendicolare all'equatore. Il primo è la metà del secondo. I 90th meridiani sono archi di cerchio mentre gli altri sono archi di ellissi che congiungono i due poli. I paralleli sono diritti ma diversamente spaziati. La scala è vera solo lungo i paralleli 40°44’ N e 40°44’ S.
Karl Brandan Mollweide (1774-1825) nacque il 03/02/1774 a Lipsia. Dopo un infanzia precoce si laureò all' Università di Halle e fù professore al Franckesche Stiftung. Durante questo periodo creò la sua proiezione. Nel 1811 lasciò Stiftung per l' Università di astronomia di Lipsia dove fù nominato professore capo ed occupò la cattedra di matematica. Fù un autorità per le scienze matematiche e sviluppò la trigonometria.
Sinusoidale: Questa proiezione fù sviluppata nel sedicesimo secolo ed usata da Cassini nel 1570 e da Jodocus Hondius nell' atlante di Mercatore prima del diciassettesimo secolo. E' la più vecchia proiezione pseudocilindrica attualmente in uso, prende spesso il nome di Sanson-Flamsteed o Proiezione Equivalente di Mercatore. E' una Proiezione equivalente con paralleli diritti egualmente spaziati intersecano il meridiano centrale, lungo la metà dell'equatore, con il giusto angolo (paralleli perpendicolari al meridiano centrale), gli altri meridiani sono curve sinusoidali egualmente spaziate che si incontrano ai poli; sono concavi verso il meridiano centrale. I poli sono punti. La proiezione è simmetrica rispetto al meridiano centrale e all' equatore. La scala è vera solo sul meridiano centrale e i paralleli, le distorsioni cominciano a farsi sentire vicino ai meridiani esterni alle alte latitudini. Questa proiezione ha un parallelo standard fittizio perchè fisso alla latitudine di 0°.0000. Spesso usata per la rappresentazione di stati con sviluppo verticale anziche orizzontale ( Cile ). Proiezione usata sin dalla metà del sedicesimo secolo
Wagner IV : Questa proiezione fù presentata da Karlheinz Wagner in 1932. Il meridiano centrale è lungo la metà dell'equatore. Gli altri meridiani sono parti di ellissi, concave verso il meridiano centrale, ugualmente spaziate. I meridiani con longitudine 103°55' Est ed Ovest sono archi di cerchio. I paralleli sono linee diritte diversamente spaziate perpendicolari al meridiano centrale. La distanza fra i paralleli aumenta avvicinandosi all'equatore. I poli sono linee lunghe la metà dell'equatore. La proiezione è equivalente. La Scala è vera solo lungo il parallelo 42°59' ed è costante lungo qualsiasi parallelo e tra ogni coppia di paralleli equidistanti dall'equatore. Le distorsioni non sono così estreme verso i meridiani esterni alle alte latitudini, ma c'è una considerevole distorsione delle regioni polari. Le distorsioni si annullano nei due punti dove i paralleli 42°59' incontrano il meridiano centrale. Questa proiezione non è nè conforme nè equidistante.
In una proiezione conica il reticolato è proiettato su un cono tangente o secante al globo lungo un piccolo cerchio ( di solito un parallelo di latitudine media rispetto alla zona da rappresentare ) . Nella versione normale i paralleli sono proiettati a formare archi di cerchio, mentre i meridiani sono proiettati come linee diritte che si irradiano ad intervalli uniformi di angolo dall’apice del cono spianato. Le proiezioni coniche non sono molto usate nelle mappe. Il caso secante che produce due paralleli standard è più frequentemente usato con le proiezioni coniche. La scala della mappa distorce rapidamente le distanze per tutti i punti che si allontano dai paralleli standard. A causa di questo problema le proiezioni coniche sono utilizzate per rappresentare zone che si sviluppano lungo i paralleli, gli Stati Uniti d’America sono frequentemente rappresentati con proiezioni coniche.
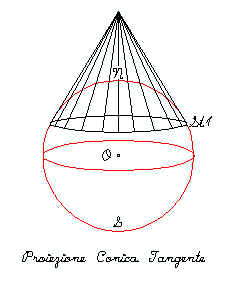Fig.11
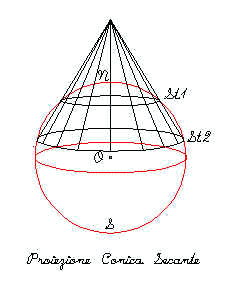Fig.12
Le principali proiezioni coniche sono:
Albers: Questa proiezione fù presentata da Heinrich Christian Albers in 1805. E' una proiezione equivalente che distorce scala e distanza eccetto lungo i paralleli standard, la scala è costante lungo qualsiasi parallelo. I paralleli sono archi di cerchio concentrici diversamente spaziati , lo spazio fra i paralleli decresce via via che ci allontaniamo dalle latitudini centrali. I meridiani sono raggi dello stesso cerchio ugualmente spaziati, tagliano i paralleli con il giusto angolo, l'angolo fra i meridiani è minore di quello vero. I poli sono archi di cerchio. Questa proiezione viene utilizzata per rappresentare regioni che si sviluppano lungo est-ovest ( Stati Uniti d’America ). Per la proiezione degli Stati Uniti vengono utilizzati i paralleli standard di 29°30'00" e 45°30'00". La proiezione non è nè conforme nè equidistante. I paralleli classici sono 15° 75°.
Bonne : Questa Proiezione data in una forma rudimentale da Claudio Tolomeo ( circa A.D. 100 ) fù successivamente sviluppata da Bernardus Sylvanus nel 1511. Il suo nome deriva dall'uso considerevole che ne fece Rigobert Bonne, specialmente nel 1752. Il Meridiano Centrale è una linea diritta. I Meridiani sono curve complesse che collegano punti ugualmente spaziati lungo ciascuno parallelo e concavi verso il Meridiano Centrale. I Paralleli sono archi circolari e concentrici spaziati alle vere distanze lungo il meridiano centrale. I Poli sono punti. La simmetria è data dal Meridiano Centrale. Questa Proiezione del tipo Pseudoconica è Equivalente. La curvatura del Parallelo Standard è identica a quello di un cono tangente a quella latitudine. Il Meridiano Centrale e il Parallelo Standard sono liberi da distorsioni. Questa proiezione non è Conforme. Ha uno Parallelo Standard che è per regola 30° N ( Il mio programma fissa il valore iniziale a 20°N ). Ha due forme limiti interessanti. Se un polo è assunto come Parallelo Standard, il risultato è la proiezione di Werner; se l'Equatore è assunto come Parallelo Standard si ottiene la Proiezione Sinusoidale.
Lambert Conformal Conic: Questa proiezione fù presentata da Johann Heinrich Lambert in 1772, è anche conosciuta come la proiezione Conica Ortomorfica. E' una proiezione conforme che distorce l’area e la forma via via che ci allontaniamo dai paralleli standard, le distorsioni sono costanti lungo qualsiasi altro parallelo.La scala è costante lungo qualsiasi parallelo ed è la stessa in ogni direzione verso un punto qualsiasi. I paralleli sono archi concentrici di cerchio diversamente spaziati, più ravvicinati vicino al centro della proiezione. I meridiani sono raggi dello stesso cerchio ugualmente spaziati, che tagliano i paralleli con il giusto angolo, l'angolo tra i meridiani è minore di quello reale. Per la proiezione degli Stati Uniti vengono utilizzati i paralleli standard di 33°00'00" e 45°00'00". La proiezione non è nè equivalente nè equidistante.
Policonica: Sviluppata nel 1820 da Ferdinando Hassler, questa proiezione è basata su un infinito numero di coni tangenti ad un infinito numero di paralleli. Il meridiano centrale è diritto mentre gli altri meridiani sono curve complesse. I paralleli sono archi di cerchio non concentrici. Tutti i meridiani sono concavi verso il meridiano centrale. I paralleli tagliano il meridiano centrale ad intervalli uguali, questi intervalli aumentano via via che ci allontaniamo dal meridiano centrale. La scala è vera solo lungo ogni parallelo e solo lungo il meridiano centrale.
Modificate
Le proiezioni modificate sono tutte quelle proiezioni che non ricadono completamente in uno dei casi precedentemente esaminati.
Hammer : Questa proiezione fù presentata da H. H. Ernst von Hammer in 1892. Questa proiezione è equivalente, il solo punto libero da distorsioni è il centro di proiezione. Ha meno distorsioni angolari nei meridiani più esterni vicino ai poli, rispetto alle proiezioni pseudocilindriche.Il meridiano centrale è una linea diritta lunga la metà dell' equatore; gli altri meridiani sono curve complesse ugualmente spaziate lungo l'equatore e concave verso il meridiano centrale. L' equatore è diritto, mentre gli altri paralleli sono curve complesse ugualmente spaziate lungo il meridiano centrale e concave verso il polo più vicino.Questa proiezione è una proiezione equivalente a bordo ellittico. E’ una modifica della proiezione Azimutale di Lambert ispirata dalla proiezione di Aitoff.
General Vertical Near/Side Perspective : Questa proiezione ( conosciuta dai Greci e dagli Egiziani circa 2000 anni fà ) è una proiezione del tipo prospettico azimutale scenografico, solo che il punto di vista V non è dalla parte opposta del centro di proiezione C , ma dalla stessa parte. Le proiezioni azimutali viste precedentemente sono delle particolari proiezioni prospettiche. La distanza fra il punto di vista V ed il centro di proiezione C è l'altezza del punto di vista aldisopra della superficie terrestre HAboveS.E' spesso usata per mostrare il pianeta come visto dallo spazio. Il meridiano ed il parallelo del centro di proiezione sono linee rette. Gli altri meridiani e paralleli sono archi di cerchio ed ellissi, ma possono essere anche parabole ed iperbole. La proiezione non è nè conforme nè equivalente. Le distorsioni maggiori sono ai limiti della zona di proiezione.
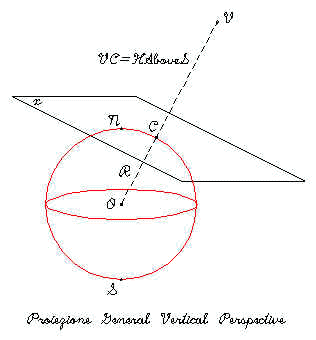Fig.13
Van der Grinten : Questa proiezione fù presentata da Alphons J. Van der Grinten in 1898. E' una proiezione che può essere classificata come policonica. Il meridiano centrale è una linea diritta mentre gli altri meridiani sono archi di cerchio spaziati ugualmente lungo l'equatore e concavi verso il meridiano centrale. L'equatore è una linea diritta, mentre gli altri paralleli sono archi di cerchio concavi verso il polo più vicino. La proiezione non è nè conforme nè equivalente. Il mondo è racchiuso in un cerchio. La scala è vera solo lungo l'equatore ed aumenta rapidamente via via che ce ne allontaniamo. Le distorsione d'area sono estreme vicino ai poli.
Interrotte
Le proiezioni interrotte sono utilizzate per rappresentare il mondo e minimizzare le distorsioni.
Goode’s Homolosine : J.P.Goode studiò questa proiezione
Pseudocilindrica composita del tipo Equivalente ( Equal Area ). I paralleli sono linee
parallele e diritte perpendicolari ai meridiani centrali. Essi sono spaziati ugualmente
tra le latitudini 40 deg 44 min N e S. Oltre queste latitudini tendono ad avvicinarsi mano
a mano che si avvicinano i poli. Tra le latitudini 40° deg 44' min N e S, i meridiani
sono curve sinusoidali ugualmente spaziate, altrimenti sono archi ellittici, concavi verso
il meridiano centrale. I meridiani sono rivolti leggermente verso le latitudini indicate.
I sei meridiani centrali sono linee diritte che hanno un valore 0.22 volte quello
dell'Equatore. L'emisfero settentrionale ha due meridiani centrali a -100° e 30° gradi
di longitudine. L'emisfero meridionale
ha i meridiani centrali alla longitudine di -160°, -60°, 20°, e 140° gradi. Il centro
della mappa è a 0° gradi di longitudine e 0° gradi di latitudine. Nell'emisfero
settentrionale, l'interruzione è posta a
-40° gradi di longitudine. Nell'emisfero meridionale le interruzioni sono poste a
-100°, -20°, e 80° gradi di longitudine. Il meridiano -180° gradi rappresenta il bordo
della proiezione. Tra le latitudini date, la scala è vera lungo ogni latitudine e lungo
il meridiano centrale. Oltre queste latitudini, la scala è identica per la latitudine di
segno opposto. I Poli sono punti.
Mollweide : E' una proiezione Pseudocilindrica del tipo
Equivalente ( Equal Area ). I Paralleli sono linee diritte diversamente spaziate più
distanziati vicino l'Equatore e perpendicolare al meridiano centrale. I Meridiani sono
archi semiellittici spaziati ugualmente che si intersecano ai poli e rivolgono la
concavità verso il meridiano centrale. Ci sono sei meridiani centrali che sono linee
diritte dai poli al Equatore. L'emisfero settentrionale ha i meridiani centrali alle
longitudini di 60°, -170°, e -30° gradi. L'emisfero meridionale ha i meridiani
centrali alle longitudini di 90°, -140°, e -20° gradi. Il centro della mappa è
posto alla longitudine -160° e alla latitudine 0° gradi.
Nell'emisfero settentrionale le interruzioni sono poste ai meridiani 110° e -100° gradi.
Nell'emisfero meridionale le interruzioni sono poste ai meridiani 140°, e -70° gradi. Il
meridiano 20° gradi rappresenta i bordi della proiezione. La Scala è vera lungo le
latitudini 40° deg 44' min N e S ed è costante lungo qualsiasi latitudine data. Essa è
la stessa per la latitudine di segno opposto. I Poli sono punti. I meridiani centrali e
l'Equatore sono elementi di simmnetria.
References
Map Projection Overview / Peter H. Dana Department of Geography
The University of Texas at Austin."Map Projections - A Working Manual" by John P. Snyder
U.S. Geological Survey Professional Paper 1395
United States Government Printing Office, Washington: 1987Aviation Formulary V1.19 by Ed William - Modified for East + and West -
WOLFRAM - RESEARCH - Eric Weisstein's world of MATHEMATICS -