Rappresentazione grafica dei risultati di un esperimento: la scelta delle scale
Imparerai ora a rappresentare graficamente i dati ottenuti mediante le tue misure.
Prendi il foglio di carta millimetrata. In esso sono riportate:
|
|
delle linee orizzontali a distanza di 1 mm. Sui bordi orizzontali sono evidenziati gruppi corrispondenti ad 1 cm; |
|
|
Delle linee verticali anche esse a distanza di 1 cm. Sui bordi verticali sono evidenziati gruppi corrispondenti ad 1 cm. |

Su questo foglio vuoi rappresentare le tue misure di massa al variare del volume.
INDICAZIONE DELLE VARIABILI E DELLE RELATIVE UNITA' DI MISURA
Riporta in corrispondenza del bordo orizzontale una parola che indichi chiaramente che su quell'asse andrai a valutare nel tuo caso specifico i VOLUMI (non dimenticare di scrivere anche le unità di misura di tale grandezza, nel caso specifico centimetri cubici).
Riporta sul bordo verticale il nome dell'altra grandezza insieme con le unità di misura. Nel caso specifico MASSA espressa in gr .
INDIVIDUAZIONE DELLE SCALE RELATIVE AI DUE ASSI
![]()
![]()
Considera i valori delle altezze riportate nella tua Tabella. Essi saranno compresi tra un valore MINIMO (Vmin) e un valore MASSIMO (Vmass).
Se vuoi ottenere un grafico con dati sperimentali "ben spaziati" ti conviene far coincidere per esempio a 2cm dell'asse orizzontale del foglio di carta millimetrata con una quantità che è prossima per esempio a (Vmin - Vmass) / 10 (cioè circa 1/10 della differenza fra il massimo ed il minimo valore del volume. Tale valore rappresenta il PASSO della tua scala orizzontale.
Attenzione: ti conviene sceglier un numero prossimo a quello calcolato in modo che tu possa valutare facilmente suoi multipli o sottomultipli.
Riporta, sull'asse orizzontale, con la matita i valori numerici dei volumi che associ ad ogni 2 cm della tua carta millimetrata: a 2 cm corrisponde come gia detto, quello stimato utilizzando le tue misure; a 4 cm corrisponderà il doppio; ... a 20 cm corrisponderà un valore che è 10 volte quello associato a 2 cm della carta millimetrata.
35. A quale volume corrisponde 1 cm della tua scala orizzontale? Corrisponde a 2 centimetri cubi.
A quale volume corrispondono 4.5 cm della tua scala orizzontale? Corrispondono a 9 centimetri cubi.
Spiega le tue conclusioni.
Ho ottenuto questi risultati secondo il valore che corrisponde al passo da me stabilito ( 2 cm sulla scala = 4 centimetri cubi).
36. Ogni millimetro della tua scala orizzontale corrisponde ad una variazione di volume di...?
Ogni millimetro della mia scala orizzontale corrisponde ad una variazione di volume di 0.2 centimetri cubi.
Spiega come sei arrivato a questa conclusione. Ho ottenuto questo risultato considerando che, secondo il passo dato, 5 mm corrispondono ad 1 cm. Dunque 1 mm è uguale ad 1/5, cioè 0.2 centimetri cubi.
Considera i valori delle masse riportati nella Tabella. Ripeti per la scelta della scala sull'asse verticale in cui riporterai le masse quanto fatto a proposito dei volumi riportati sull'asse orizzontale.
Se desideri un grafico ben spaziato ti conviene far corrispondere ad ogni 2 cm della carta millimetrata una massa (circa) uguale alla differenza fra il valore massimo della massima (Mmass) e il valore minimo della massa (Mmin) da te misurato diviso 10 [= (Mmin - Mmass) /10]. Tale valore rappresenta il PASSO della tua scala verticale.
Naturalmente fa in modo che tale valore sia espresso con un numero di cui si possono facilmente calcolare i multipli e i sottomultipli del tipo 5 gr, 10 gr... e NON 22 gr, 37 gr.
37. A quale massa corrisponde il PASSO da te stimato? Corrisponde a 10 gr.
Riporta sull'asse verticale i valori di massa corrispondenti a 2 cm, 4cm,... 20cm (cioè multipli della quantità da te stimata).
38. A quale massa corrisponde 1 cm della tua scala verticale? Corrisponde a 5 gr.
A quale massa corrispondono 7.5 cm della tua scala verticale? Corrispondono a 37.5 cm.
39.Ogni millimetro della tua scala verticale corrisponde ad una variazione di massa di...? Ogni millimetro della mia scala verticale corrisponde ad una variazione di massa di 0.5 gr.
Spiega come sei arrivato a questa conclusione. Ho ottenuto questo risultato considerando che, secondo il passo dato, 5 mm corrispondono a 2.5 gr. Dunque 1 mm e uguale ad 1/5, cioè 0.5 gr.
Naturalmente per la scelta delle scale sui due assi (orizzontale e verticale) avresti potuto procedere diversamente.

![]()
Per esempio se desideri un grafico più compatto puoi far corrispondere a 1 cm dell'asse orizzontale (verticale) ad un volume (ad una massa) pari al PASSO calcolato per l'asse orizzontale (verticale). Ovviamente i multipli del PASSO corrisponderebbero a 2 cm, 3 cm... 10 cm.
40. Se avessi fatto questa scelta a che valore di massa corrisponderebbero 3.5 cm dell'asse verticale? Corrisponderebbero a 7 gr.
A che valore di volume corrisponderebbero 4.7 cm dell'asse orizzontale? Corrisponderebbero a 9.4 centimetri quadri.
Motiva la tua risposta. Avendo tenuto in considerazione il passo del volume (2cm = 0.4 centimetri cubi), ho moltiplicato per le due grandezze la lunghezza in millimetri di 1/5 di un centimetro cubo, cioè 0.2 centimetri cubi, che corrispondono ad 1 mm sulla scala.
RAPPRESENTAZIONE DEI DATI SPERIMENTALI SUL GRAFICO
Nota che ad ogni tabella dei tuoi dati corrisponde ad una coppia di misure (massa e volume). Ogni coppia sarà rappresentata sulla carta millimetrata mediante un punto.
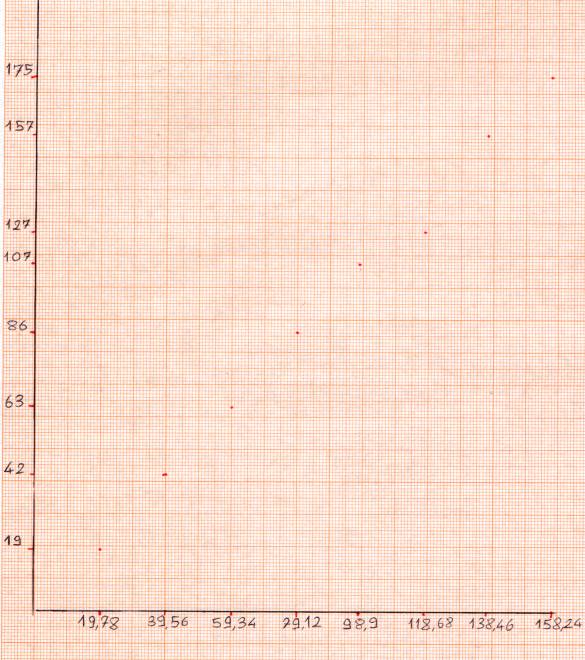
Considera i valori di massa e volume riportati nella prima riga della colonna della tabella.
Individua sull'asse orizzontale,con buona approssimazione,la posizione corrispondente al volume.
Spostandoti in direzione verticale individua,guardando la scala verticale,la posizione corrispondente al valore della massa.
Segna in modo chiaro con un punto (ben "marcato") la posizione rappresentativa dei due valori (altezza-massa) della prima misura.

Si dice che tale punto P è individuato da una coppia di valori e si scrive P = (volume-massa) che si possono facilmente ottenere considerando:
|
|
La perpendicolare condotta dal punto P all'asse orizzontale delle altezze. L'intercetta corrisponde al valore dell'altezza associato a P; |
|
|
La perpendicolare condotta dal punto P all'asse verticale delle masse. L'intercetta corrisponde al valore dell'altezza associato a P; |
Rappresenta ora sulla carta millimetrata tutte le altre coppie di misure (volume-massa)riportate in tabella alla 2,3...8 riga.
L'insieme dei punti riportati costituiscono la RAPPRESENTAZIONE GRAFICA dei risultati delle misure.
41)Noti qualche regolarità nella rappresentazione grafica dei dati? Esprimila a parole.
Ho notato che tutti i punti vanno a formare una retta.
42)Immagina,senza farlo in realtà, di voler disegnare sulla carta millimetrata una curva che "passi più o meno bene" vicino ai tuoi dati sperimentali riportati come punto sul grafico. Quale forma dovrebbe avere questa curva?
Prendi un righello e traccia la retta che più si avvicina ai tuoi dati sperimentali:si dice che hai INTERPOLATO i tuoi dati con una curva nota,la retta appunto.

La retta che hai appena tracciato ti può servire a valutare,per esempio,senza in realtà fare la misura nella quale la massa corrisponde un certo volume o a quale volume corrisponde una certa massa.
43)Utilizzando la retta d'interpolazione sai stimare a quale massa corrisponde un volume di 22cm? E viceversa a quale massa corrisponde un volume di 83gr? Descrivi la procedura che hai utilizzato.
 VOLUME
=22cm
VOLUME
=22cm
 MASSA
= 83g
MASSA
= 83g
44)Se invece del cilindro che hai in dotazione ne avessi usato uno di diametro diverso ,ritieni che avresti ottenuto la stessa rappresentazione grafica? Motiva chiaramente la tua risposta risposta.

45)La procedura di estrapolazione si basa su qualche ipotesi? Quale?
In genere le procedura di estrapolazione si basano sull'ipotesi che, per valori più piccoli/più grandi di quelli misurati le grandezze seguano lo stesso tipo di dipendenze/relazione evidenziato nell'intervallo di valori corrispondente alle misure realmente effettuate.