sei sul sito di Anna e Giovanni

7) La curva di crescita

Sarebbe utile individuare una funzione matematica, che chiameremo POS%(t), con:

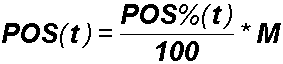
che consenta di determinare il numero dei nuovi positivi agli esami diagnostici successivi al primo, indipendentemente dal fatto di ripetere lo screening esattamente un lead time dopo.

Relativamente all’esempio proposto, ripetere lo screening non 1 anno dopo, ma ad esempio 3 mesi dopo il primo, potrebbe garantire una effettiva anticipazione diagnostica come minino di 9 mesi a tutti i nuovi positivi.

Ebbene, il numero di tali nuovi positivi:

potrebbe determinarsi, grazie a POS%(t), facendo:

Con riferimento all’esempio (se=90), può intanto osservarsi che caratteristica peculiare della funzione cercata è che:





Se ciò vale per un intervallo di tempo pari ad 1 anno, sembra naturale che debba valere anche per un intervallo più piccolo.

Una funzione che ha tali requisiti è la funzione:

con:

Qualunque sia t (ad esempio tm) è infatti:

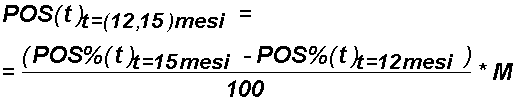
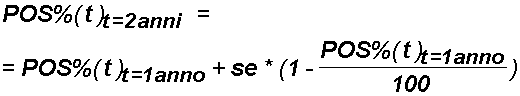
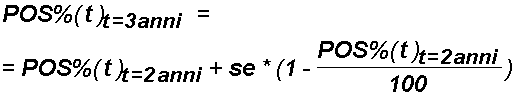
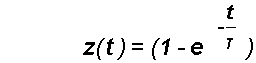
E'pertanto: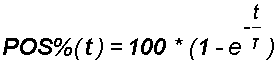

.

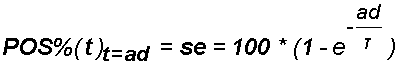
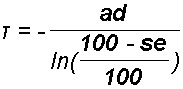
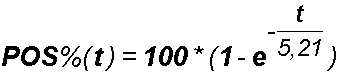
La determinazione della costante di tempo t può farsi non appena è nota l’anticipazione diagnostica (ad); ponendo infatti:

è:

Mentre la durata della fase preclinica (dfp) può calcolarsi facendo: dfp=(6,91*t), dato che per t=(6,91*t) č POS%(t)=99,9.

Nel caso di specie, essendo se=90 e ad=12 mesi, è: t =5,21 mesi, dfp=36 mesi e:


Inoltre, verificare (come si è fatto) che 180 malati (pari al 90% di M=200, essendo ) sono subito identificati al primo screening, è come dire che, nell’ultimo anno (dei tre) della fase preclinica, la malattia del singolo paziente percorre gli ultimi 90 stadi (N%(t) varia da 10 a 100).

Verificare che occorre attendere 1 anno per identificare altri 18 malati (pari al 9% di M=200), è come dire che, nel secondo anno della fase preclinica, la malattia del singolo paziente percorre 9 stadi (N%(t) varia da 1 a 10).

Verificare che occorre attendere ancora 1 anno per identificare gli ultimi 2 malati (pari all’1% di M=200), è come dire che, nel primo anno della fase preclinica, la malattia del singolo paziente percorre solo 1 stadio (N%(t) varia da 0 a 1).

La crescita neoplastica preclinica N%(t) è dunque legata alla POS%(t) nello specifico dalla relazione N%(t)=100-POS%(36-t) e, in generale, dalla relazione N%(t)=100-POS%(dfp-t).

Il profilo matematico della storia biologica di uno specifico tumore nella fase preclinica può allora esplicitarsi nella: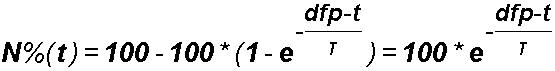

(vedi fig.6).



utenti in questo momento connessi alla rete di siti web di Giovanni Fraterno: