Verso l’infinito

“<<sai contare?>> chiese la Regina Bianca.<<Quanto fa uno più uno più uno più uno più uno più uno più uno più uno?>>.<<Non lo so>> disse Alice. <<Ho perso il conto>>.”

Lewis Carroll, Alice nel Paese delle Meraviglie

I paradossi di Zenone

“Gli studiosi di greco sono dei privilegiati; alcuni di loro conoscono il greco, e la maggior parte di questi non conosce nient’altro”

Gorge Bernhard Shaw

Prendiamo in considerazione una freccia che deve raggiungere una destinazione finale. Per raggiungere la sua destinazione la freccia deve compiere prima metà della distanza compresa fra l’arciere e il bersaglio, poi la metà della distanza che resta, poi la metà della metà, e così via, all’infinito.

La feccia arriverà alla sua destinazione soltanto dopo aver percorso una distanza infinita!!!!! E già! Infatti il tutto può essere rappresentato dalla seguente serie infinita:

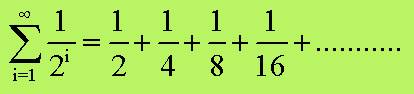
che è la serie geometrica di ragione ½ , quindi la sua somma infinita vale 1.

NOTA SULLA SERIE GEOMETRICA:

Serie indeterminate

“Le serie divergenti sono un’invenzione del diavolo, ed è una vergogna fondare su di esse qualsiasi dimostrazione”

Niels Henrik Abel

“L’eternità è molto noiosa, soprattutto verso la fine”

Woody Allen

Altri famosi paradossi hanno a che fare con le serie indeterminate, alcune delle quali hanno sviato i più grandi matematici. Si consideri la seguente serie:

S = 1 – 1 + 1 – 1 + 1 – 1 + 1 - ………

Da questa serie segue:

- S = - 1 + 1 – 1 + 1 – 1 + 1 – 1 + 1 – 1 + ….

Disponiamo le due serie nel seguente modo:

S = 1 – 1 + 1 – 1 + 1 – 1 + 1 - ………

- S = - 1 + 1 – 1 + 1 – 1 + 1 –…….

Sottraendo la riga inferiore da quella superiore, otteniamo

S-(-S)=2S=1

Cioè

S = ½

Possiamo anche riscrivere la serie originale come:

S = (1 – 1) + (1 – 1) + (1 – 1) + ………

che fa zero, o anche come:

S = 1 + (– 1 + 1) + (– 1 + 1) + ………

Che fa uno.

In base al modo in cui viene manipolata algebricamente, la serie vale 1 , 0 o ½. La serie è cioè indeterminata, e non può essere uguagliata ad alcuno dei tre valori.

Serie armonica

“Anche dopo esservi stati anni diecimila, come il sole brillando luminosi per innalzare a Dio preghiere, non meno giorni abbiam di fila di quando la prima volta iniziammo festosi”

Amazing Grace, gospel

Un’altra famosa serie che sconcertò intere generazioni di matematici è conosciuta come serie armonica:

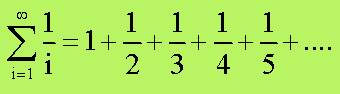
Nel quattordicesimo secolo, il dotto francese Nicola di Oresme, autore del Tractatus de figuratione potentiarum et mensurarum, dimostrò che la serie armonica è divergente, cioè che tende all’infinito quando il numero dei suoi termini tende all’infinito.

La sua dimostrazione fu ottenuta raggruppando i termini della serie nel modo seguente:

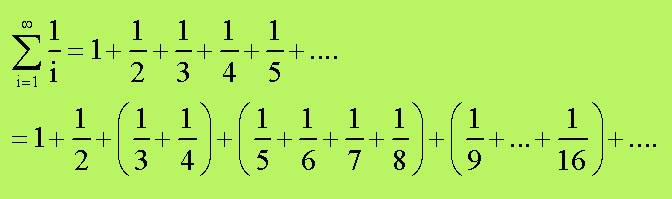
Si costruisca una seconda serie sostituendo ogni denominatore all’interno di ogni parentesi sopra con il massimo denominatore presente all’interno della parentesi stessa. Dunque:

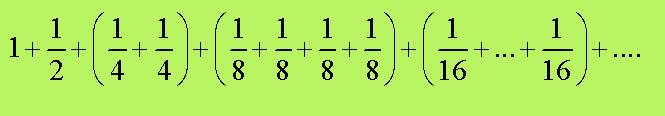
Ovviamente, la somma all’interno di una qualsiasi parentesi della seconda serie è minore della corrispondente somma nella prima serie. Ne consegue che la seconda serie è minore della prima. Dato che le somme fra parentesi nella seconda sono tutte uguali a 1/2 , è chiaro che la seconda diverge. Di conseguenza anche la prima diverge, nonostante il fatto che i suoi termini siano infinitesimali. La proprietà dei termini successivi di una serie di essere progressivamente decrescenti, non costituisce dunque una condizione sufficiente per la convergenza.

Quindi:

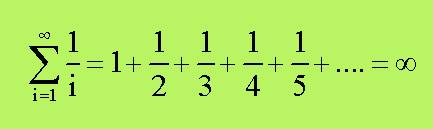
Bibliografia: “Il numero” di Midhat Gazalè

Home - Matematica - Archivio