Leibniz e il triangolo armonico

“La facoltà che mette in moto l’invenzione matematica non è il ragionamento, bensì l’immaginazione”

Augustus De Morgan

Gottfried Wilhelm Leibniz

Nato a Lipsia, fece studi di teologia, legge, filosofia e matematica: per questo viene descritto come l’ultimo grande erudito dotato di conoscenze universali. Il tratto più caratteristico della personalità di Leibniz è la fede in un ordine del mondo, dinamico e aperto all’invenzione e alla possibilità.

Il problema e la soluzione

Nel 1676 Leibniz visitò Londra per la seconda volta. Huygens gli aveva proposto il problema di trovare la somma dei reciproci dei numeri triangolari: ossia,

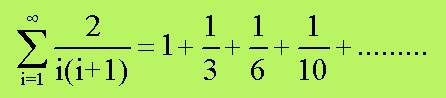
Utilizzando un trucchetto Leibniz scrisse ciascun termine come somma di due frazioni:

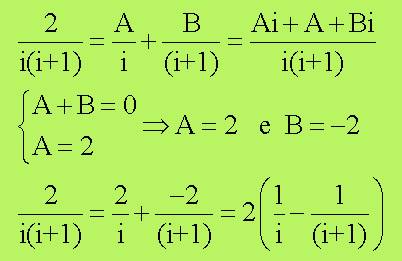
quindi ho:

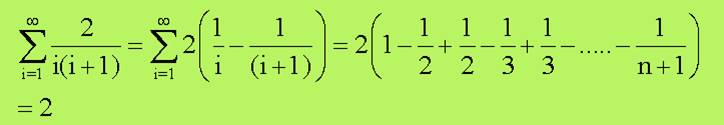
I termini in mezzo se ne vanno (perché opposti) e quindi per n che tende all’infinito rimane 1-0 che moltiplica 2 quindi 2 è la somma infinita della serie.

Questo successo lo indusse a credere ingenuamente che sarebbe stato in grado di trovare la somma di qualsiasi serie infinita. La somma di serie fece poi di nuovo la sua comparsa a proposito del triangolo armonico, le cui analogie con il triangolo aritmetico di Pascal affascinavano Leibniz.

TRIANGOLO ARITMETICO TRIANGOLO ARMONICO

Nel triangolo aritmetico ciascun elemento (tranne quelli che si trovano nella prima colonna) è uguale alla differenza tra il termine immediatamente al di sotto di esso e quello alla sinistra di quest’ultimo; nel triangolo armonico ciascun termine (tranne quelli che si trovano nella prima fila) è uguale alla differenza tra il termine immediatamente al di sopra di esso e il termine alla destra di quest’ultimo. Inoltre nel triangolo aritmetico ciascun elemento (tranne quelli che si trovano nella prima colonna o nella prima fila) è uguale alla somma di tutti i termini della linea sovrastante che vanno da quello immediatamente al di sopra di esso verso sinistra, mentre nel triangolo armonico ciascun elemento è uguale alla somma di tutti i termini della linea sottostante che vanno dal termine immediatamente al di sotto di esso verso destra. Poiché in quest’ultimo caso il numero dei termini è infinito, Leibniz ebbe modo di esercitarsi nel calcolare somme di serie infinite. La serie della prima riga è la serie armonica, che diverge; su tutte le altre righe la serie converge. I numeri della seconda riga sono la metà dei reciproci dei numeri triangolari, e Leibniz sapeva che la somma di questa serie è uguale a 1. I numeri della terza riga sono un terzo dei reciproci dei numeri piramidali:

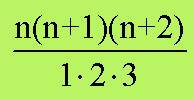
e il triangolo armonico mostra che la somma di questa serie è uguale a 1/2 ; i numeri della quarta fila sono un quarto dei reciproci dei numeri figurati corrispondenti all’analogo quadri-dimensionale del tetraedro, e la loro somma è uguale a 1/3 ; e così via, per tutte le righe successive del triangolo armonico. I numeri della n-esima fila diagonale di questo triangolo sono i reciproci dei numeri della corrispondente n-esima riga diagonale del triangolo aritmetico divisi per n.

Bibliografia:“Storia della matematica” di Carl B. Boyer Oscar saggi mondadori

Home - Matematica - Archivio