La storia dei
numeri
![]()
“Un matematico, come
un pittore o un poeta, è un costruttore di forme. Le forme del
matematico, come quelle del pittore o del poeta, devono essere meravigliose; le
idee, come i colori o le parole, devono accordarsi le une alle altre in
armonia”
G.W.Hardy
Sistemi di
numerazione arcaici
“Vorrei sapere,
oggi, tanto quanto pensavo di sapere dieci anni fa.”
Otto Neugebauer
“… i numeri
aumentano fino a dieci, e poi da uno ancora ricomincia
il loro ritmo.”
Ovidio, Fasti 3
1)Gli egiziani
Gli antichi egizi svilupparono un sistema di numerazione decimale semplice e di facile
utilizzo, e inventarono un sistema di moltiplicazione a base 2 simile a quello
usato dai nostri moderni computer. Gli egiziani sapevano elevare al quadrato,
estrarre le radici quadrate, e determinare la somma di progressioni aritmetiche
e geometriche. Sapevano calcolare superfici di triangoli e trapezi, così
come il volume di un tronco di piramide quadrata. Utilizzavano funzioni
trigonometriche ed inoltre uguagliarono l’area di un cerchio con un
diametro di 9 unità a quella di un quadrato il cui lato misura 8
unità, il che equivale ad attribuire al moderno p un valore pari a (4/3)4 » 3.1605.
Sistema di numerazione egiziano (sono qui
riportate solo le prime sette potenze di dieci):
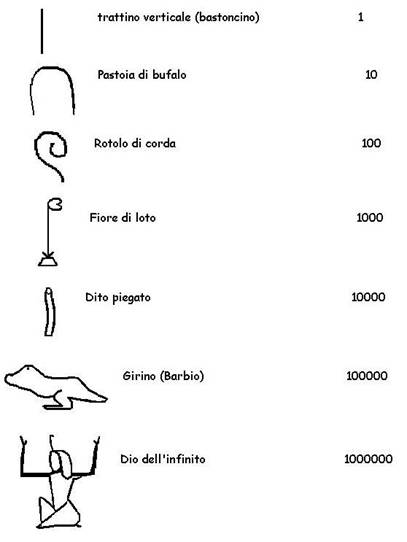
Esempi di numeri scritti con i simboli
egiziani:
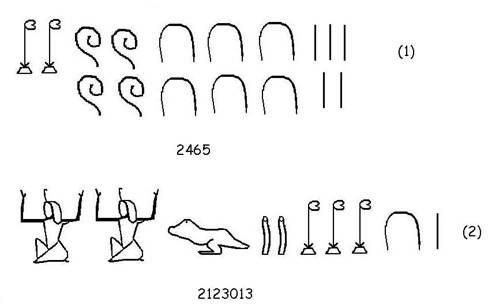
La (1) significa che è il numero
2465, mentre il (2) rappresenta il numero 2123013, questo secondo esempio inoltre
rivela l’assenza dello zero. Lo schema di numerazione degli egiziani
incarna il sistema additivo decimale, dove esiste uno specifico simbolo per
ogni potenza di dieci, e dove non più di nove simboli di un dato tipo
appaiono in una qualunque rappresentazione numerica.
2)I babilonesi
Intorno al

e la <<coda di rondine>>:

che denotavano rispettivamente 1 e 10 . Questi
erano giustapposti in piccoli raggruppamenti compatti, che rappresentavano i
numeri da
Esempi di raggruppamenti di numeri
cuneiformi:
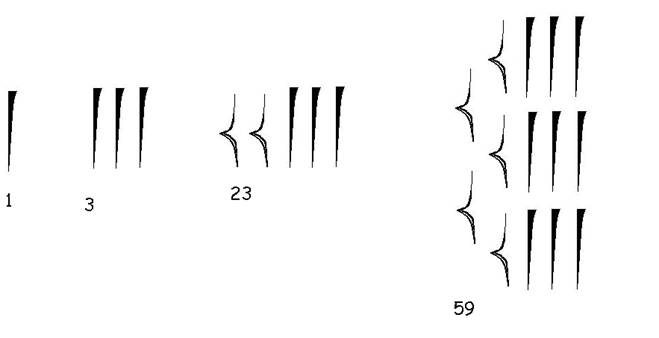
Qui invece riporto l’esempio del
numero 2165012:

10X603 +
1X602
+
23X60 +
32X1
= 2165012
Lo
zero rimase assente fino a un periodo compreso fra il
Nel frattempo, gli scribi si sforzavano
di lasciare uno spazio vuoto là dove mancava una potenza di 60.
Ovviamente se lo scriba era distratto tale sistema poteva portare a serie
ambiguità, come in figura:

NOTA: i Babilonesi erano familiari con il
cosiddetto teorema di Pitagora. Oggigiorno quasi tutti concordano
nell’affermare che Pitagora, che trascorse molti anni in Mesopotamia,
molto probabilmente aveva imparato dai suoi maestri babilonesi il teorema che
porta il suo nome.
3)I Greci
A dispetto dei notevoli contributi
all’aritmetica, i Greci non furono in grado di produrre un sistema di
numerazione che i posteri avrebbero conservato. Il sistema adottato era
additivo in base 10, e le singole lettere dell’alfabeto erano usate per
rappresentare sia le nove cifre da
Comunque il sistema non era facile da
utilizzare, neppure per eseguire operazioni aritmetiche elementari come
addizione o moltiplicazione. I calcoli più complicati venivano eseguiti
con l’ausilio dell’abaco, oppure ricorrendo a tavole della
moltiplicazione e della divisione, così difficili da imparare che solo i
più esperti matematici sapevano utilizzare con maestria.
4)Il sistema di
numerazione decimale
Colui che più di tutti
contribuì all’introduzione del sistema indo-arabico in Occidente
fu senza dubbio Leonardo da Pisa (1180-1250), altrimenti
conosciuto come FIBONACCI. Figlio di Bonaccio, governatore pisano di Bougie in
Algeria, Leonardo iniziò lo studio del calcolo ,
studium abaci, sotto la guida di un arabo che egli descrisse come uno
straordinario maestro. Nel 1202, Fibonacci pubblicò il suo importante
Liber Abaci, che iniziava con queste parole:<<Le nove figure indiane sono
9 8 7 6 5 4 3 2 1
Con queste figure e con il segno 0, che
in arabo è chiamato zefiro, può essere scritto qualunque
numero>>.
Bibliografia: preso da “Il numero “ di M.
Gazalé edizioni dedalo.
Home - Matematica - Archivio