L’invenzione
dei logaritmi
![]()
“Non è la
conoscenza, ma l'atto di imparare; non il possesso ma l'atto di arrivarci, che
dà la gioia maggiore. Quando ho chiarito e esaurito un argomento, mi ci
allontano, per tornare nell'oscurità; l'uomo non soddisfatto è
così strano, che se ha completato una struttura non ce la fa a restarci
in pace, ma deve iniziarne un'altra. Immagino che si debba sentir così il
conquistatore del mondo che, quando un regno è stato a malapena
conquistato, si lancia subito verso un altro.”
Johann Carl Friedrich Gauss
“Tu, natura, sei la
mia dea; alle tue leggi si legano i miei servizi...”
Johann Carl Friedrich Gauss
“poche cose, ma mature”
Johann Carl Friedrich Gauss
John Napier
John Napier(
Giovanni Nepero), non era un matematico di
professione. Era un ricco proprietario terriero scozzese di famiglia nobile che
passava il suo tempo amministrando i suoi vasti possedimenti e scrivendo su
svariati argomenti. Si interessava soltanto a certi aspetti della matematica,
soprattutto a quelli che si riferivano al computo e alla trigonometria. Napier stesso
ci informa di avere lavorato alla sua invenzione dei logaritmi per venti anni,
prima di pubblicare i risultati, affermazione che farebbe risalire
l’origine della sua idea al 1594.
L’idea
centrale
L’idea centrale su cui si basava
l’invenzione del Napier
può essere spiegata molto semplicemente. Per mantenere molto vicini tra loro
i termini di una progressione geometrica delle potenze intere di un dato numero
è necessario assumere come numero dato una cifra molto vicina
all’uno. Napier decise pertanto di usare come
numero di base 1-10-7 (ossia, 0.9999999).
Ora i termini della progressione delle potenze crescenti sono effettivamente
molto vicini tra loro, anzi troppo vicini. Per ottenere un maggiore equilibrio
e per evitare cifre decimali Napier moltiplicò
ciascuna potenza per
107 . Ossia, se
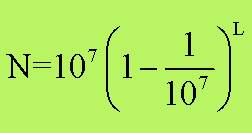
allora L è il “logaritmo”
neperiano del numero N. Così il logaritmo di 107 era 0, il logaritmo di:

era 1, e così via. Se egli avesse
diviso per 107 i numeri e i
logaritmi, si sarebbe virtualmente ottenuto un sistema di logaritmi con la base
1/e: infatti:

è vicino a

Va ricordato però, che a Napier era estraneo qualsiasi concetto di un sistema di
logaritmi: la sua definizione era, infatti, diversa dalla nostra. I principi
della sua regola meravigliosa venivano da lui spiegati in termini geometrici
nel modo seguente. Siano dati un segmento lineare AB e una semiretta o
semiraggio CDE ….
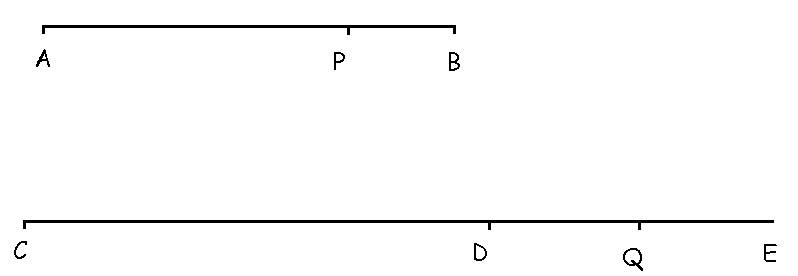
Un punto P parta da A e si muova lungo AB
con velocità variabile decrescente in rapporto alla sua distanza da B;
contemporaneamente un punto Q partendo da C cominci a muoversi lungo CDE
… con velocità costante uguale a quella che P aveva
all’inizio del suo moto. Napier chiamava questa
distanza variabile CQ il logaritmo della distanza PB.
La descrizione geometrica di Napier corrisponde, naturalmente, alla descrizione numerica
che abbiamo dato sopra. Per mostrare questa corrispondenza, facciamo PB = x e
CQ = y . Se si prende AB uguale a 107,
allora abbiamo, in notazione moderna:

Allora

ossia:
![]()
ove c in base alle condizioni limite iniziali
risulta essere uguale a 10-7
. Pertanto:

ossia:

In altri termini, se le distanze PB e CQ
fossero divise per 107 , la definizione di Napier porterebbe esattamente a un sistema di logaritmi con
base 1/e, come si è
accennato precedentemente. Napier non aveva nessuna
idea di una base per il suo sistema, tuttavia compilò le sue tavole
mediante ripetute moltiplicazioni, equivalente a potenze di 0.9999999.
Ovviamente la potenza (o numero) decresce con il crescere dell’indice ( o
logaritmo). Ciò non sorprende, giacché egli usava una base 1/e
che è minore di 1.
La pubblicazione
Il sistema dei logaritmi pubblicato nel
1614 ebbe un immediato riconoscimento, e fra gli ammiratori più
entusiasti v’era Henry Briggs professore di
geometria a Oxford. I due si trovarono in Scozia e discussero su alcune modifiche
da apportare al metodo dei logaritmi.
Briggs propose di utilizzare potenze di 10 e Napier si dichiarò d’accordo.
Il concetto il logaritmo continuò ad
evolvere negli anni successivi fino oggi.
Henry Briggs e Napier avevano in mente ancora molte idee ma John Napier non aveva più l’energia necessaria per
metterle in pratica e
morì nel 1617.
Bibliografia: “Storia della matematica” di Carl B. Boyer Oscar saggi mondadori
Home - Matematica - Archivio