Integrale gaussiano, soluzione di Laplace

“ In fondo la teoria delle probabilità e’ soltanto senso comune espresso in numeri ”

Laplace

Laplace ai suoi tempi era considerato, come matematico, altrettanto grande di Lagrange. Professore all’École Polytechnique, ma diversamente da Monge e da Lagrange non pubblicò i testi delle sue lezioni. Le sue pubblicazioni concernevano principalmente la meccanica celeste: in questo campo egli si affermò come la figura più significativa del periodo successivo a Newton. In campo matematico si occupò della teoria della probabilità. A partire dal 1774 scrisse numerose memorie sull’argomento, raccogliendo poi i risultati via via raggiunti nel suo classico trattato Théorie analytique des probabilités del 1812. Questo trattato , però, rivela la mano di un grande analista che conosce bene l’analisi superiore. Essa è piena di integrali che comportano funzioni beta e gamma, e Laplace fu tra i primi a mostrare che:

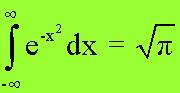
Il metodo con cui si ottenne questo risultato era abbastanza artificioso ma comunque non molto diverso dal moderno metodo di trasformare in coordinate polari:

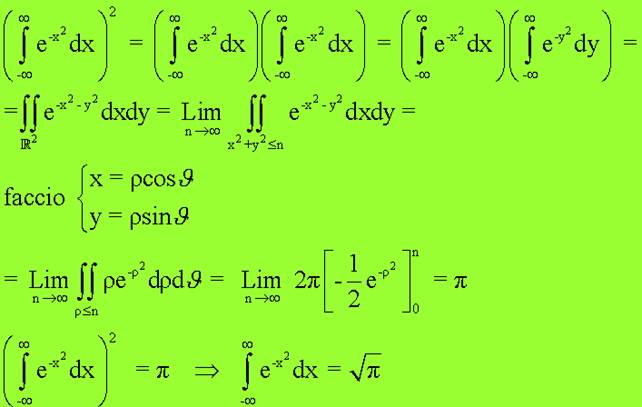
La tecnica delle coordinate polari prevede la sostituzione fatta sopra con il calcolo dello Jacobiano che in questo caso risulta essere uguale a r.Ovviamente l’angolo varia tra 0 e 2p.

Bibliografia: “Storia della matematica” di Carl B.Boyer

Home - Matematica - Archivio