Gauss e la sua maestra

“È comunque un grande piacere, dopo aver girato a lungo attorno a una verità, trovare il modo più semplice e diretto di dimostrarla.”

Johann Carl Friedrich Gauss

“Intendo la parola dimostrazione non nel senso degli avvocati, i quali stabiliscono che due mezze dimostrazioni ne uguagliano una intera, ma nel senso di un matematico, dove mezza dimostrazione = 0, ed è richiesto per la dimostrazione che ogni dubbio diventi impossibile.”

Johann Carl Friedrich Gauss

Da fanciullo Gauss frequentò la scuola locale, dove l’insegnante aveva fama di essere molto esigente nei riguardi dei suoi allievi. Un giorno, per tenerli occupati, assegnò loro l’esercizio di sommare tutti i numeri da uno a cento, chiedendo che ciascuno deponesse la sua lavagnetta su un tavolo non appena avesse finito il calcolo. Quasi immediatamente Carl depose sul tavolo la propria lavagnetta dicendo “ ecco fatto ”; l’insegnante diede un’occhiata sprezzante mentre gli altri continuavano a fare i calcoli. Alla fine l’insegnante esaminò i risultati e trovò che la lavagnetta di Gauss era l’unica a presentare il risultato esatto, 5050 senza nessun calcolo.

Il trucco che utilizzò Gauss fu di utilizzare la seguente formula:

La formula permette di calcolare la somma dei primi m numeri. Ipotizziamo infatti di dover calcolare la somma dei primi m numeri, scriviamone alcuni:

per m = 0 la somma vale 0

per m = 1 la somma vale 0 + 1 = 1

per m = 2 la somma vale 0 + 1 + 2 = 3

per m = 3 la somma vale 0 + 1 + 2 + 3 = 6

……………. ………………………………………………………….

Cerchiamo un funzione S(m) che ci restituisca la somma per determinati valori di m. Per prima cosa proviamo con un polinomio omogeneo perché per m = 0 la S(m) = 0. Si può osservare immediatamente che per un polinomio omogeneo di primo grado senza termine noto (cioè S(m) = km, dove k è costante) la cosa non funziona. Proviamo a considerare un polinomio omogeneo di secondo grado con due coefficienti da determinarsi:

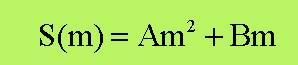
determiniamo A e B risolvendo il sistema:

quindi:

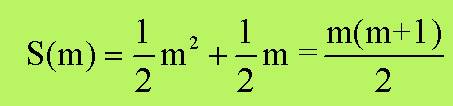
allora possiamo dire che:

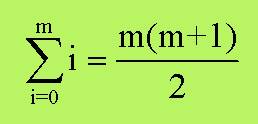
Dimostriamo per induzione che la formula vale per ogni m maggiore uguale a 0:

(lo stesso gioco si può fare per la somma dei quadrati dei primi numeri ma occorrerà usare un polinomio omogeneo di terzo grado)

Bibliografia: “Storia della matematica” di Carl B. Boyer

Home - Matematica - Archivio