L’epoca di Eulero

“Ci sono alcuni misteri che la mente umana non penetrerà mai. Per convincercene non dobbiamo fare altro che gettare un’occhiata alle tavole dei numeri primi. Ci accorgeremo che non regna ne ordine ne legge”.

Leonhard Euler

La vita di Eulero

Il padre di Eulero era un pastore protestante che, come il padre di Jacques Bernoulli, sperava che il figlio entrasse nella carriera ecclesiastica. Il giovane Eulero, però, studiò sotto la guida di Jean Bernoulli, collaborò con i suoi figli Nicolaus e Daniel, e attraverso costoro scoperse la propria vocazione. Godette di un’educazione di vasto respiro, poiché allo studio della matematica aggiunse quello della teologia, della medicina, dell’astronomia, della fisica e delle lingue orientali. Nel 1730 Eulero si trovò ad occupare all’accademia di Pietroburgo la cattedra di filosofia naturale. All’età di 26 anni si ritrova ad essere il matematico più importante dell’accademia. Sposatosi, si dedicò alla pura ricerca matematica, e ad allevare una famiglia di tredici figli. Nel 1735 aveva perduto la vista dell’occhio destro, riguardo questo fatto lo stesso Eulero si pronunciò:<< così avrò minor occasione di distrarmi>>. Durante la sua vita pubblicò più di 500 lavori, tra libri e articoli, e per quasi mezzo secolo dopo la sua morte fra le pubblicazioni dell’Accademia di Pietroburgo continuavano ad apparire i suoi lavori. Eulero morì a 76 anni improvvisamente mentre prendeva il tè in compagnia di uno dei suoi nipoti.

La somma dei reciproci dei quadrati perfetti

“Il matematico è assolutamente libero, entro i limiti della sua immaginazione, di costruire i mondi che più gli piacciono. Quello che immagina è materiale per il suo capriccio e basta; infatti non sta scoprendo nuovi principi fondamentali dell'universo né si sta avvicinando alla conoscenza di Dio. Se riesce a trovare, sperimentalmente, insiemi di entità che obbediscono allo stesso schema logico delle sue entità matematiche, allora ha applicato la sua matematica al mondo esterno; ha creato una nuova branca delle scienze.”

William Navin Sullivan

Uno dei problemi che Eulero affrontò fu di riuscire a determinare la seguente somma infinita:

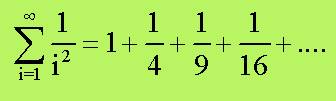
Eulero prese le mosse dal noto sviluppo in serie:

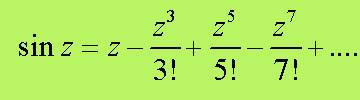
L’uguaglianza sin(z)=0 poteva allora essere concepita come l’equazione polinomia infinita:

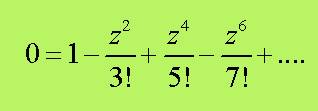
(ottenuta dividendo tutto per z), oppure, sostituendo z² con w, come l’equazione:

In base alla teoria delle equazioni algebriche è noto che, se il termine costante è 1, la somma dei reciproci delle radici è uguale al coefficiente del termine lineare cambiato di segno: in questo caso 1 / (3!). Si sa, inoltre, che le radici dell’equazione nell’incognita z sono date da p,2p,3p, e così via; pertanto le radici dell’equazione nell’incognita w sono p²,(2p)²,(3p)², e così via. Dunque:

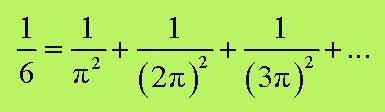
ossia

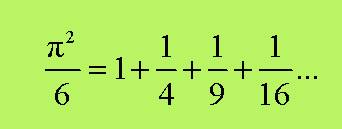
La formula di Eulero

“Chi non apre con devozione un libro di matematica e non lo legge come la parola di Dio, costui non l'intende.”

Friedrich Leopold von Hardenberg

Una formula molto importante scoperta da Eulero è la seguente:

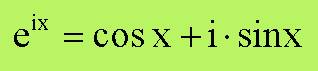
dove i = (-1)^(1/2) è il numero immaginario.

Se poi pongo x = p ottengo la relazione di Eulero (una formula di estrema bellezza):

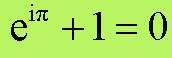
La formula lega i cinque numeri più importanti della matematica : 0, 1 , i, e, p .

Dimostriamo la formula di Eulero partendo dallo sviluppo in serie dell’ esponenziale:

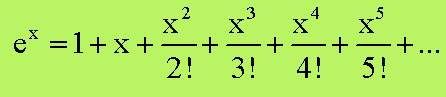
quindi esprimendo e^(ix) ho che:

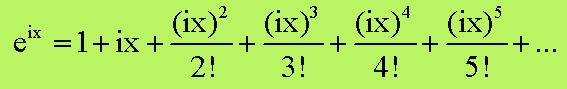
sviluppando le potenze e raggruppando gli i ho:

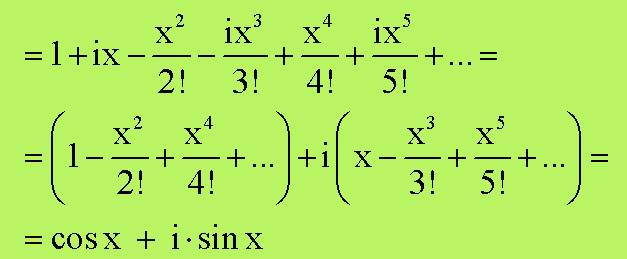
Riconoscendo lo sviluppo le coseno nella prima parentesi e lo sviluppo del seno nella seconda ho trovato la formula di Eulero.

Bibliografia: “Storia della matematica” di Carl B.Boyer

Home - Matematica - Archivio