PREPARAZIONE COMPITO 3d
4.11.03
1)
le disequazioni

-13/5<x<=-1
 scrivi le soluzioni nell’ipotesi che k sia maggiore di 8
scrivi le soluzioni nell’ipotesi che k sia maggiore di 8
x<2 v 4<x<k/2
e se ci sono i valori assoluti?
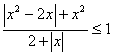
(1-r(17))/4<=x<=2
2)
la geometria analitica
a) condurre per il punto C dell’asse x, equidistante dai punti A(-2,2) e B(0,-4) la retta r parallela ad AB e per B la retta t parallela alla bisettrice del 1° e 3° quadrante. Determinare le coordinate del punto D, comune a r e t e la misura del perimetro del triangolo BCD.
(5/2,-3/2) 1/4(4r(5)+r(10)+5r(2))
b) i lati di un triangolo hanno per equazione 4x+5y = 1, 2x+y= 5, y = 1. Verificare che le bisettrici dei suoi tre lati s’incontrano in un unico punto di cui si richiedono le coordinate e determinare il raggio della circonferenza inscritta nel triangolo
c)
dato il fascio di rette di equazione (2+k)x+(k-1)y+3-k=0 determina
i.
le rette generatrici e il centro del fascio (-2/3,5/3)
ii.
il valore di k della retta del fascio parallela alla retta
passante per A(2,1) e per B(0,3) e giustificare il risultato ottenuto
iii.
i valori di k per i quali vi sono rette del fascio che
formano angoli ottusi con l’asse x (k<-2 v k>1)
iv.
i valori di k per i quali le rette del fascio intersecano il
segmento OC di estremi O(0,0) e C(2,0) (k<=-7vk>=3)
d) in un sistema di riferimento cartesiano xOy scrivere le equazioni della traslazione che porta l’origine del riferimento nel punto O’ comune alle due rette r e s di equazioni y = 3x e 2y=-x+2 (o spostare il punto di intersezione nell’origine O degli assi). In questo nuovo sistema di riferimento x’O’y’ considera la generica retta di equazione x’=h che interseca la retta r in A e la s in B. Determina per quale valore di h l’area del triangolo ABOè uguale a 7 (dove O non è O’).
h=(-1+-r(197))/7
fine