COMPITO DI MATEMATICA – 5D - 31.1.04 

CLICCA SUI BOTTONI ACCANTO AL NUMERO DEL PROBLEMA

1)      Studia la funzione 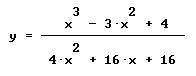 e disegna il grafico. Determina e disegna la tangente nel punto di flesso. Aiutandoti con il grafico della funzione, determina quante soluzioni reali ha l’equazione: al variare di m (consiglio: esplicita m)

2)      E’ data l’equazione . Determina i coefficienti in modo che abbia un stremante in  e un flesso in . Disegna il grafico della funzione ottenuta.  Trasla la curva in modo che il flesso coincida con l’origine degli assi. La nuova curva ottenuta che proprietà ha riguardo a simmetrie particolari? Cosa ne concludi?

Scegli tre tra i seguenti quesiti:

1)      Tre giocatori tirano ad un bersaglio. E’ data la variabile aleatoria X : “numero di colpi a segno”. Determinarne la tabella sapendo che le probabilità dei tre giocatori di mettere colpire il bersaglio sono rispettivamente , e .

2)      Un giocatore paga una posta di 1 €. Vince se escono, nel lancio di due dadi, due facce uguali. Quanto deve essere la vincita se il gioco è equo? (costruire una variabile aleatoria che rappresenti la situazione e dare motivazioni sufficienti)

3)      Un’urna contiene 7 gettoni (indistinguibili al tatto) Uno porta la cifra 0, due portano la cifra 1, due la cifra 2, due la cifra 3. Considera la variabile aleatoria X somma dei numeri che compaiono su due gettoni estratti. Calcola e poni sotto forma di tabella la distruzione di probabilità della variabile X e calcola il valore medio.

4)      E’ data la funzione . Calcolane l’asintoto obliquo se esiste.

5)      Si devono mettere in comunicazione due capannoni adiacenti creando un’apertura di forma rettangolare sormontata da un arco semicircolare. Sapendo che il perimetro del rettangolo è fisso ed è di m.11 stabilisci quali devono essere le dimensioni dell’apertura in modo che, nel complesso, la regione aperta sia la più grande possibile.

6)      Un algoritmo genera numeri casuali di 3 cifre (si considerano significativi anche i numeri che iniziano per 0). Qual è la probabilità che venga generato un numero che contiene almeno due volte il numero 5?